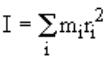
La determinazione della struttura molecolare:

 spettri rotazionali e vibrazionali

I livelli energetici di una molecola “scaturiscono” dalla propria rotazione globale, dalle vibrazioni relative degli atomi e dai cambi nella sua configurazione elettronica.

La presenza delle righe spettrali di origine molecolare è spiegabile allo stesso modo delle righe spettrali atomiche: quando una molecola (o atomo) transisce da uno stato contraddistinto da un certo valore di energia a uno stato inferiore, il surplus di energia viene emesso sotto forma di un fotone avente una precisa frequenza. Esistono tuttavia delle sostanziali differenze fra spettroscopia molecolare e spettroscopia atomica dovute alla maggiore varietà dei modi in cui può variare l’energia delle molecole rispetto agli atomi isolati. Infatti l’energia globale di un sistema molecolare non muta solo in funzione delle transizioni elettroniche da un orbitale all’altro, bensì anche a seguito di modifiche negli stati vibrazionali e rotazionali della molecola.

Analizzando uno spettro molecolare si possono ottenere informazioni riguardanti l’energia e le distanze di legame della molecola e quindi anche la sua forma. Tuttavia, mentre è possibile ottenere uno spettro rotazionale puro, lo spettro vibrazionale comprende anche righe dovute alle contemporanee variazioni di natura rotazionale.

Sperimentalmente esistono tre diversi modi per ottenere spettri molecolari:

1.     La Spettroscopia di emissione viene osservata quando una molecola transisce da un certo stato energetico E” ad uno inferiore E’ (energia inferiore) emettendo l’energia corrispondente alla differenza fra i livelli sotto forma di un fotone avente una frequenza n coincidente con

n = (E” - E’)/h

dove h = 6.626 · 10^-34 J·s indica la costante di Plank.

2.     La Spettroscopia di assorbimento consiste nell’osservare le frequenze in corrispondenza delle quali la radiazione incidente è assorbita dal materiale in esame. Se per esempio la molecola si trova nel più basso livello energetico possibile (stato fondamentale), e assorbe una radiazione di lunghezza d’onda l = 470 nm (l = c/n, con c velocità della luce), allora esiste uno stato eccitato accessibile corrispondente a 2.6 eV ( 21000 cm^-1 se in funzione del numero d’onda s = 1/l) al di sopra di quello fondamentale.

3.     La Spettroscopia Raman studia i livelli energetici molecolari esaminando la luce diffusa dalle molecole. Quando la collisione fra un raggio di luce incidente, di determinata frequenza,  e le molecole del materiale provoca la diffusione, compaiono nuove frequenze causate dall’acquisto o perdita di energia da parte del fotone durante la collisone. Infatti se la luce incidente eccita le molecole, i fotoni perderanno parte della loro energia e la luce diffusa emergerà con frequenze minori dell’originale. Se al contrario, prima che vengano colpite dalla luce le molecole sono già eccitate, esse possono cedere energia ai fotoni incidenti che quindi compariranno nella radiazione diffusa sotto forma di luce a frequenza superiore.

Livelli energetici e spettri rotazionali

In un campione in fase gassosa, le molecole sono in continuo movimento dovutoto all’energia termica. Parte di questa si manifesta sotto forma di energia cinetica rotazionale associata appunto alle rotazioni relative ad un osservatore solidale al sistema di riferimento di laboratorio.

Per una singola e isolata molecola, questo moto è quantizzato in accordo con la teoria quantistica e le transizioni fra tali livelli rotazionali danno luogo allo spettro rotazionale della molecola in esame. Gli stati quantici di una molecola rimangono ben definiti quando essa è isolata, infatti a causa di collisioni con altre molecole essa può cambiare il suo stato rotazionale perturbando e modificando il suo spettro.

A patto che il tempo fra le collisioni sia lungo rispetto all’inverso della frequenza di transizione (dell’ordine di 10^-10 s), lo spettro rotazionale sarà nettamente definito. Questa condizione è facilmente realizzata nei gas a bassa pressione, meno di 10^-4 atmosfere, infatti nei gas a più alta pressione come nei liquidi, la frequenza delle collisioni è così elevata che le righe spettrali risultano tanto larghe da non poter distinguere le singole transizioni. Nello stato solido, l’orientamento delle singole molecole è pressoché fisso nello spazio e l’energia non può essere “immagazzinata” sotto forma di energia rotazionale. Di conseguenza, la spettroscopia rotazionale è usata per studiare gas a bassa pressione cercando di limitare al minimo l’allargamento di riga dovuto ad una pressione troppo elevata e all’effetto Doppler.

I livelli energetici rotazionali si possono ottenere risolvendo l’equazione di Scrodinger per la molecola oppure seguendo un approccio classico e quantizzandone il risultato.

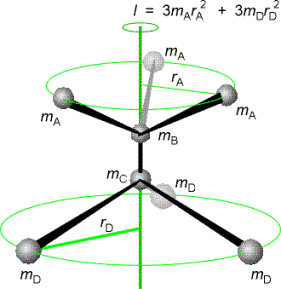
Il parametro chiave per descrivere gli spettri rotazionali è il Momento d’Inerzia della molecola.

Esso è definito come la sommatoria della massa di ogni atomo moltiplicata per il quadrato della sua distanza dall’asse di rotazione passante per il centro di massa della molecola:

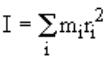
dove r_i è la distanza (ortogonale) dell’i-esimo atomo dall’asse di rotazione (Vedi figura a lato).

Poiché il momento d’inerzia dipende da tutte le masse e dalla geometria della molecola si intuisce facilmente come la spettroscopia rotazionale da informazioni riguardo gli angoli e le distanze di legame. In generale, le proprietà rotazionali di ogni molecola possono essere espresse in termini del momento d’inerzia attorno a tre assi perpendicolari scelti nella molecola. La convenzione è di chiamare i momenti d’inerzia I_a, I_b, e I_c, con gli assi scelti in modo che I_c ³ I_b ³ I_a (vedi figura in basso).

Per le molecole lineari il momento d’inerzia attorno all’asse internucleare (congiungente i nuclei) è zero, poiché r è zero. La tabella allegata indica il 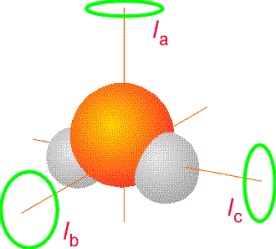momento d’inerzia per molti differenti tipi di molecole.

Considereremo per semplicità che tutte le molecole

siano rotatori rigidi cioè che non cambino le mutue

distanze fra due punti fissati durante e non la rota-

zione. I rotatori rigidi possono essere classificati in

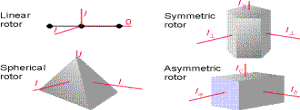
quattro differenti classi:

Rotore sferico; rotore simmetrico; rotore lineare;

rotore asimmetrico.

Classicamente, l’energia di un corpo rigido rotante intorno ad un certo asse a si esprime mediante la relazione:

dove I_a è appunto il momento d’inerzia del corpo rigido e w_a è la velocità angolare intorno all’asse scelto misurata in radianti al secondo. Un corpo rigido libero di ruotare intorno ai tre assi ha ovviamente un’energia rotazionale totale data dalla:

Il momento angolare classico di un corpo avente momento d’inerzia I_a e velocità angolare w_a è:

di conseguenza, l’energia in funzione del momento angolare intorno a ciascun asse risulta:

Da questa equazione ricaveremo i livelli energetici rotazionali per i rotatori rigidi esclusi quelli asimmetrici il cui calcolo è noioso e complicato.

Livelli energetici di un rotatore sferico

Per un rotatore sferico, come ad esempio la molecola del metano (CH₄),  il valore del momento d’inerzia intorno ai tre assi ortogonali coincide e l’espressione classica dell’energia si riduce a:

E = (1/ 2I) (J_a² + J_b² + J_c²) = J²/2I

con J² quadrato della grandezza (vettore) classica momento angolare totale. La corrispondente espressione quantistica si ottiene considerando che il momento angolare totale si limita ad assumere i valori

dove h coincide con h/2p. Ne risulta che l'energia di una molecola tipo rotatore sferico può assumere i valori:

Il fattore h² / 2I viene detto costante rotazionale della molecola e si indica con B, per cui:

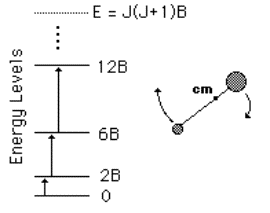
      E_J = BJ(J + 1)                     J = 0,1,2,….

L’intervallo energetico fra due livelli rotazionali adiacenti risulta:

E_J – E_{J -1} = 2BJ

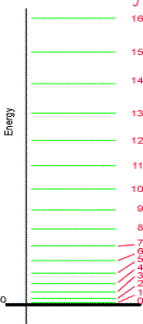E’ importante notare che la costante rotazionale B decresce all’aumentare del momento d’inerzia della molecola, di conseguenza i livelli energetici rotazionali saranno più vicini per le molecole di grandi dimensioni. Come esempio consideriamo appunto il caso del metano: dalla lunghezza dei legami e dalla massa degli atomi si ottiene un momento d’inerzia di 4.85 x 10^-45 Kg m², per cui B = 1.15 x 10^-24 joule, ovvero 0.058 cm^-1. L’intervallo energetico è dell’ordine di 1.2 cm^-1 quando J è circa 10, il che corrisponde a fotoni della regione spettrale delle microonde. Anche per gli altri tipi di molecole l’ordine di grandezza dell’energia è più o meno uguale, ed è per questo motivo che lo studio delle transizioni rotazionali pure costituisce un ramo della spettroscopia a microonde.

Livelli energetici di un rotore simmetrico

Nei rotori simmetrici, molecole tipo ammoniaca (NH₃), due momenti d’inerzia sono uguali ma differenti dal terzo I_a = I_b ¹ I_c, come per un cilindro. L’unico asse di simmetria della molecola è il suo asse principale, il momento d’inerzia attorno a tale asse lo denoteremo con  e i due momenti d’inerzia eguali con . Se  >  il rotore è classificato come “oblate” (schiacciato ai poli come il benzene C₆H₆), viceversa verrà chiamato “prolate” (allungato come il cloruro di metile CH₃Cl). Con queste considerazioni l’espressione classica dell’energia per tale molecola diventa:

espressione che può essere riscritta in termini del quadrato del modulo del momento angolare

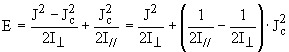
L’espressione quantica si ottiene effettuando la “consueta” sostituzione discreta:

Sappiamo inoltre dalla meccanica quantistica che le componenti del momento angolare lungo un qualunque asse sono quantizzate e limitate a valori interi multipli di h; di conseguenza il momento angolare intorno l’asse principale (asse c) è circoscritto ad assumere valori Kh con K = 0, ± 1, ± 2, ..., ± J. Nell’espressione dell’energia, quindi, sostituiamo a J_c la quantità Kh, ottenendo :

E(J,K) = BJ(J+1) +(A – B) K²

Con    A = h²/ 2   e    B = h²/ 2.

Notiamo che adesso l’energia rotazionale dipende da due numeri quantici J e K 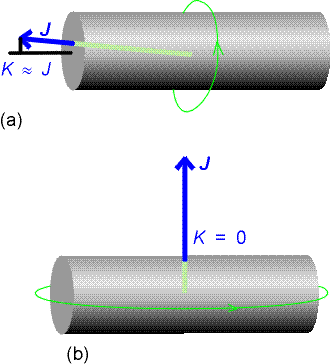poiché ci sono due distinti momenti d’inerzia per la molecola. L’importanza di K è dovuta al fatto che l’energia di rotazione dipende dalla particolare distribuzione del momento angolare totale. Quando K = 0 non c’è componente del momento angolare lungo l’asse principale (vedi figura (b)), il moto assume interamente la caratteristica del testacoda e l’energia dipende solamente da .Se invece K = ± J la rotazione molecolare ha luogo maggiormente intorno all’asse di simmetria (vedi figura (a)) e i livelli energetici dipendono quasi interamente da .

Si noti inoltre che il segno di K non influisce sull’energia (dipende infatti da K²) perché opposti valori di K corrispondono a sensi opposti nella rotazione della molecola e l’energia è indipendente dalla direzione della rotazione.

Livelli energetici di un rotore lineare (molecole biatomiche)

Per i rotori lineari, come le molecole biatomiche dell’anidride carbonica (CO₂), la rotazione avviene solamente intorno ad un asse ortogonale alla congiungente i nuclei e il momento angolare riferito a tale congiungente è nullo poiché è nullo il momento d’inerzia sempre riferito a tale asse. Di conseguenza la componente del momento angolare intorno all’asse principale di un rotore lineare è identicamente nulla e sarà nullo anche K. I livelli energetici di una molecola biatomica saranno allora dati dalla seguente espressione:

E(J) = BJ(J+1)              J = 0,1,2….

Dove la costante rotazionale della molecola B = h² / 2I con I unico momento d’inerzia della molecola ().

Tale espressione dell’energia è identica a quella del rotore simmetrico ma qui K = 0 mentre per il rotore sferico l’espressione finale è dovuta al fatto che A = B.

Regole di selezione per le transizioni rotazionali

La principale regola di selezione per l’osservazione di un puro spettro rotazionale è che la molecola abbia un momento di dipolo permanente. Poiché all’origine di un’onda elettromagnetica di frequenza n si può sempre pensare che ci sia un dipolo elettrico oscillante alla medesima frequenza, solamente le molecole dotate di momento dipolare elettrico permanente sono suscettibili di emettere o di assorbire la radiazione subendo una transizione fra stati rotazionali differenti. Le molecole dotate di un momento di dipolo elettrico permanente sono chiamate polari ed interagiscono (si accoppiano), al contrario di quelle non-polari, con un campo elettromagnetico attraverso il 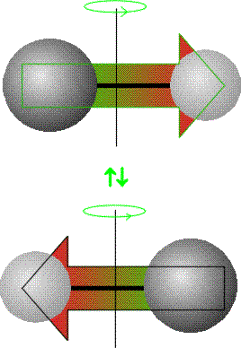campo generato dalla propria rotazione (del tutto analoga ad un dipolo oscillante).

Questo concetto è mostrato nella figura a lato dove per un osservatore, una molecola polare rotante sembra un dipolo oscillante capace di interagire con un campo elettromagnetico.

Non si avrà dunque uno spettro rotazionale puro per tutte le molecole biatomiche omonucleari (O₂, N₂) e per i rotori lineari che sono definiti pertanto rotazionalmente inattivi. I rotori sferici invece sono rotazionalmente inattivi se non vengono “distorti” da forze rotazionali che vanno a modificare la loro distribuzione di carica.

Per calcolare le variazioni ammissibili nel valore di J e K pensiamo al fatto che il fotone è dotato di momento angolare di spin, e quando viene espulso o assorbito dalla molecola, nel corso di una transizione rotazionale, il momento angolare della molecola deve mutare adeguatamente per compensare quello fotonico (conservazione del momento angolare globale di un sistema). Essendo unitario il momento angolare di spin del fotone, anche la conseguente variazione del momento angolare 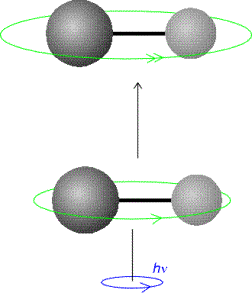molecolare che accompagna la transizione dovrà essere unitaria. La regola di selezione sarà quindi:

DJ = ± 1

La transizione DJ = + 1 corrisponde all’assorbimento di un fotone da parte della molecola (figura a lato) se sta ruotando nello stesso senso dello spin del fotone incidente. Invece la transizione DJ = - 1 corrisponde all'emissione di un fotone. Per i rotori simmetrici, poiché la luce non è in grado di accelerare la rotazione intorno al loro asse di simmetria, esiste un’ulteriore regola di selezione:

DK = 0

E’ da sottolineare inoltre che l’intensità della radiazione emessa o assorbita è direttamente proporzionale al quadrato del momento dipolare elettrico permanente quindi, le molecole polari con momento più elevato daranno uno spettro con righe più intense di quelle delle molecole polari con momento minore.

Applicando le regole di selezione descritte all’espressione dell’energia, si possono calcolare le frequenze di assorbimento permesse per le transizioni  J + 1 ? J :

E = hn = 2B (J + 1)       J = 0,1,2,....

Lo spettro risulta essere suddiviso da una serie di righe di frequenze successive 2B, 4B, 6B….tutte separate di 2B (vedi figura seguente). Misurando tale distanza fra le righe (calcolato cioè B), si ricava il momento d’inerzia perpendicolare all’asse di simmetria della molecola e, note le masse degli atomi presenti nella molecola, è facile risalire alle informazione riguardanti quest’ultima come distanze, angoli di legame e quindi alla sua forma, anche se manca il valore dell’altro momento d’inerzia il cui calcolo può essere sviluppato con altri metodi.

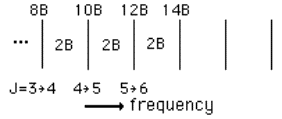
Intensità e larghezza delle righe spettrali

Analizzando gli spettri di diverse molecole ci si rende conto che l’intensità delle righe è la più varia. Una certa molecola possiede livelli energetici separati da uno specifico DE, ma capita chela frequenza associata a tale transizione non si rivela; questo perché l’intensità delle righe dipende dal numero delle molecole che si trovano nei diversi stati al momento in cui si registra lo spettro e di quale sia la “predisposizione” delle singole molecole di assorbire o emettere fotoni. Sappiamo dalle regole di selezione che DJ = ± 1, ma è più probabile la transizione J = 0 ® J = 1 o la transizione J = 4 ® J = 5 ? La meccanica quantistica “insegna” che tutte le transizioni con un uguale variazione di J sono equiprobabili tuttavia, come già detto, questo non significa che tutte le righe di uno spettro rotazionale sono ugualmente intense. Esistono due fattori che determinano e influenzano l’intensità di tali righe: la popolazione e la  degenerazione caratteristiche di ogni livello energetico.

La popolazione indica il numero di molecole che si trovano in quel determinato stato energetico; per un campione di gas alla temperatura assoluta T ed avente un numero di molecole N, la porzione di molecole aventi energia E_J, è data dalla statistica di Boltzmann. E’ noto che l’energia rotazionale del più basso stato di una molecola è zero poiché J = 0, quindi se abbiamo N₀ molecole nel più basso stato, il numero di molecole N_J in uno stato più alto J, è dato da:

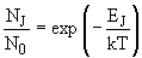
Per capire meglio, consideriamo un campione a temperatura ambiente (T = 300 K), che corrisponde ad un energia termica kT = 200 cm^-1; i livelli molecolari rotazionali distano fra di loro solitamente di una frazione di cm^-1 e anche a temperatura ambiente sono in parecchi ad essere popolati. La conseguenza ovvia è che le righe componenti lo spettro di assorbimento rotazionale, si devono a transizioni delle molecole originanti da una serie di stati rotazionali popolati. Possiamo  graficare la relativa popolazione in funzione di J per una data temperatura e per valori diversi della costante rotazionale B:

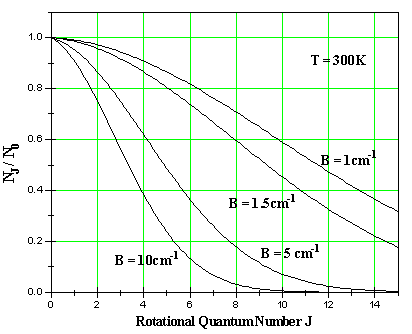
La degenerazione (dei livelli) consiste nell’avere diversi livelli energetici caratterizzati dalla stessa energia, di conseguenza una transizione fra tali livelli non implica un’emissione o assorbimento di radiazione. Dalla meccanica quantistica è noto che per un dato valore del momento angolare totale J, ci sono (2J + 1) possibili valori per M_J. Ogni livello energetico rotazionale ha (2J + 1) livelli della stessa energia. Cioè, lo stato rotazionale J = 0 è un livello energetico singolo (singoletto), lo stato J = 1 è un triplo livello energetico (tripletto) e così via. Quindi sebbene la popolazione molecolare di ogni livello energetico rotazionale diminuisce esponenzialmente con l’aumentare di J, il numero dei possibili livelli aumenta 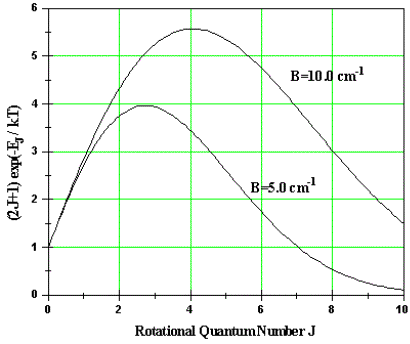linearmente con J. La popolazione totale relativa di un livello con energia E_J diventa quindi:

La figura a lato mostra appunto la popolazione relativa, tenendo conto della degenerazione dei livelli, in funzione di J per due differenti valori di B. Si noti che la curva presenta un massimo per un certo valore di J; tale massimo è naturalmente funzione della temperatura.

In conclusione possiamo affermare che l’intensità delle righe spettrali è proporzionale alla temperatura di lavoro, alle popolazioni dei livelli energetici rotazionali e alla degenerazione di tali livelli. Transizioni fra livelli con valori molto bassi o molto alti di J, saranno caratterizzate da una riga spettrale meno intensa rispetto a quelle per cui il valore di J presenta un massimo (come in figura).

Le varie righe dello spettro hanno inoltre una differente larghezza.

Uno dei fenomeni responsabile di ciò è l’effetto Doppler ; quando una sorgente di radiazioni di lunghezza d’onda l si allontana dall’osservatore con velocità v, l’osservatore rivela una radiazione con lunghezza d’onda (1 + v/c) l, dove c rappresenta la velocità della luce. Una parte delle molecole del campione in esame si allontanano dall’osservatore, altre si avvicinano, alcune si muovono velocemente, altre lentamente. Come conseguenza si ha che la forma della riga rivelata rappresenta il profilo di assorbimento o di emissione che scaturisce dall’insieme degli spostamenti per effetto Doppler verificatisi nel campione. Poiché la percentuale di molecole che presentano una determinata velocità è data dalla distribuzione di Maxwell, la cui curva è una gaussiana, la forma di una riga Doppler è data appunto da una curva gaussiana i cui parametri (larghezza e altezza) variano molto con la temperatura perché varia con essa la distribuzione delle velocità molecolari (vedi figura). La larghezza a metà altezza di una riga risulta essere Dl = 2(l c) (2kT ln 2/m)^1/2.

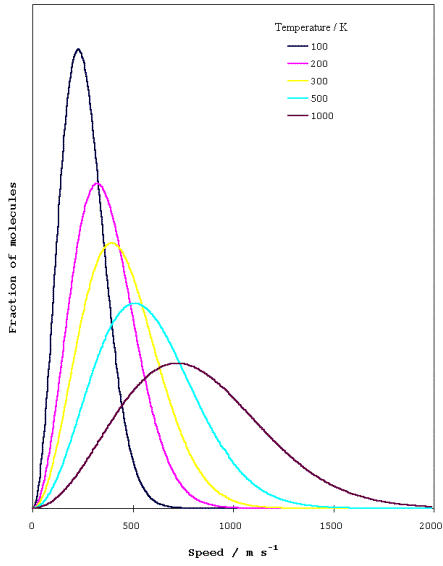
Per ottenere delle righe di nitidezza massima è opportuno operare a bassa temperatura ed eliminare così l’allargamento Doppler. Ma anche quando questo è divenuto trascurabile, agisce un altro fenomeno chiamato allargamento naturale. Esso dipende dal tempo di vita del livello energetico. Se lo stato del sistema varia alla velocità 1/t, i suoi livelli energetici appaiono indistinti in una misura dell’ordine di dE dove dE ~ h /t. Cioè se una molecola rimane nel suo stato eccitato per un tempo uguale a t, la sua energia risulta E ± dE. Solo nel caso in cui lo stato in esame avesse vita infinitamente lunga sarebbe possibile determinarne con esattezza l’energia corrispondente. Da ciò emerge che le righe spettrali si estendono sopra un intero arco di frequenze e gli stati eccitati a vita breve sono caratterizzati da righe larghe, quelli a vita lunga da righe più strette.

Livelli energetici e spettri vibrazionali

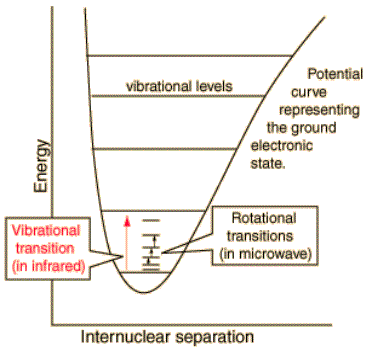
Consideriamo per semplicità una molecola biatomica, le cui vibrazioni si riducono unicamente allo stiramento (stretching) e alla contrazione dei legami. Nella formazione di una molecola stabile, si verifica un bilanciamento di forze, repulsiva fra la carica positiva dei nuclei atomici e fra ogni coppia di elettroni, attrattiva fra il nucleo di un atomo e gli elettroni dell’altro. I due atomi si stabilizzano ad una media distanza internucleare alla quale si ha un bilanciamento delle forze e l’energia totale del sistema presenta un minimo: il sistema è in equilibrio. Spingendo con forza gli atomi per stare più vicini, la forza repulsiva subirà un rapido aumento, al contrario cercando di allontanare gli atomi si avrà una resistenza da parte della forza attrattiva. In entrambi i casi per distorcere il legame c’è bisogno di energia. E’ possibile graficare l’energia in funzione della distanza internucleare come nel seguente grafico in cui, considerata la molecola biatomica dell’acido cloridrico ( o cloruro di idrogeno, HCl), l’atomo di cloro è fissato all’asse delle ordinate ed immaginiamo di spingere e tirare l’atomo d’idrogeno più vicino o più lontano (dalla distanza di equilibrio). Maggiore è la forza impressa in un verso o nell’altro, maggiore risulta l’incremento energetico il cui valore risulta nullo solo nella posizione di equilibrio corrispondente alla distanza di legame della molecola:

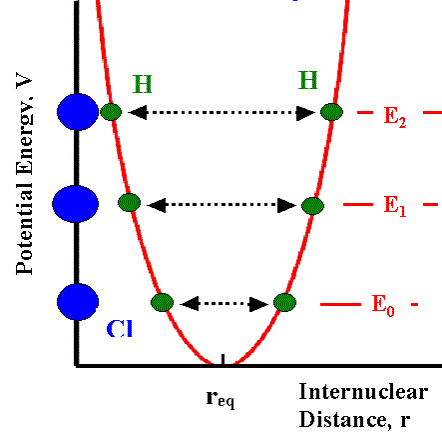
Tale grafico mostra appunto una tipica curva dell’energia potenziale di una molecola biatomica. Nelle regioni vicine a r_eq (minimo della curva), l’energia potenziale può essere approssimata ad una parabola, quindi possiamo scrivere:

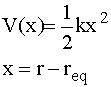
dove k rappresenta la costante elastica di forza del legame. Più ripido è il potenziale (più rigido è il legame), più elevato è il valore della costante elastica. Essendo questo potenziale coincidente con quello di un oscillatore armonico semplice, nella molecola deve persistere un’oscillazione armonica semplice intorno alla posizione di equilibrio del legame ed inoltre i livelli energetici vibrazionali permessi risultano:

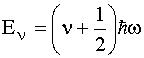            con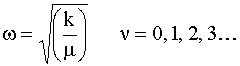         

dove m è la massa ridotta (o massa effettiva) della molecola uguale a:

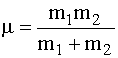
Però tali livelli energetici non sono che un’approssimazione dei veri livelli, in quanto dovuti all’approssimazione parabolica della curva dell’energia potenziale; infatti quando l’energia delle vibrazioni è tale da imporre agli atomi un considerevole spostamento dalla posizione di equilibrio del legame, l’approssimazione parabolica perde di significato: essa non consente di dissociare la molecola nei suoi atomi componenti ne di avvicinarli indefinitamente. Alle alte frequenze vibrazionali i contorni del potenziale risultano meno ristretti e ci si attende che ad alta energia, gli intervalli fra i livelli energetici vibrazionali siano minori che a bassa energia (vedi figura seguente); in tale situazione le oscillazioni degli atomi consentono alla molecola di “esplorare” regioni della curva dell’energia potenziale dove l’approssimazione parabolica come già detto perde di significato e sono richiesti 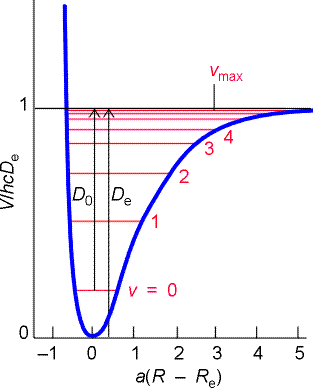termini addizionali per descrivere tale stato.

Il moto vibrazionale diventa quindi anarmonico e una forma matematica che si accosta bene alla reale curva dell’energia potenziale è stata suggerita da Morse, il cui potenziale risulta:

dove a è

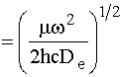
e D_e rappresenta la profondità del minimo dell’energia potenziale. D₀ rappresenta l’energia di dissociazione della molecola cioè, l’energia necessaria per rompere il legame molecolare partendo da una molecola biatomica nello stato vibrazionale n = 0. L’espressione energetica dei livelli dovuti ad un tale potenziale diventa:

E_n = (n + ½) hw – (n + ½)² x_e hw

In cui la costante di anarmonicità x_e è uguale a:

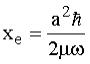
Il fatto che il secondo termine venga sottratto dal primo conferma il previsto convergere dei livelli energetici vibrazionali all’aumentare dell’energia (numeri quantici vibrazionali).

Regole di selezione per le transizioni vibrazionali

Lo stiramento o il piegamento dei legami molecolari cui origina la vibrazione della molecola possono o meno far variare il momento di dipolo posseduto dalla stessa molecola. Tale dipolo oscillante (più o meno armonicamente) consente l’emissione o l’assorbimento di radiazione elettromagnetica. Ci sono tuttavia delle vibrazioni che non alterano il momento di dipolo molecolare, come il moto di stretching nelle molecole biatomiche omonucleari, non interagendo di conseguenza con la radiazione e neanche generandola.

Infatti lo stiramento del legame fra gli atomi di una molecola biatomica omonucleare non altera il valore (nullo) del momento dipolare, quindi le molecole biatomiche omonucleari non presentano alcuno spettro vibrazionale (infrared inactive). Al contrario nelle molecole biatomiche eteronucleari, il momento dipolare varia al variare della distanza di legame; di conseguenza tali molecole sono in grado di fornire uno spettro vibrazionale sia in assorbimento che in emissione (infrared active).

Quindi la più evidente regola di selezione per le vibrazioni molecolari è che il momento di dipolo elettrico di una molecola deve cambiare quando gli atomi vengono spostati relativamente l’uno rispetto all’altro.

Tuttavia non è necessario che le molecole abbiano un momento di dipolo permanente diverso da zero per transire fra livelli vibrazionali permessi, infatti il loro momento dipolare può passare da zero a un valore diverso da zero.

La regola di selezione specifica per un oscillatore armonico è :

D n = ± 1

ottenuta dalla conservazione del momento angolare applicata al sistema molecola+fotone. L’espressione dei livelli energetici risulta quindi:

DE = hw

che tenendo conto dell’anarmonicità diventa:

DE = hw - 2(n + 1) x_e hw - ...

L’energia in più o in meno si manifesta sotto forma di un fotone la cui frequenza è tipica della regione infrarossa dello spettro della luce, da qui la denominazione di infrared active or inactive per le molecole che presentano o meno uno spettro vibrazionale. A temperatura ambiente, kT = 200 cm^-1, la maggior parte delle molecole si trova nel proprio stato vibrazionale fondamentale, pertanto la transizione dominante, risulta in spettroscopia I.R. quella da n = 0 a n = 1.

Poiché le vibrazioni possono risultare lievemente anarmoniche, bisogna considerare che le energie di transizione dipendono in piccola misura da n e che viene infranta la regola di selezione (basata sul moto armonico) e diventano possibili transizioni con 

D n = ± 2

chiamate  seconde armoniche al pari delle transizioni con D n = ± 1 dette prime armoniche o fondamentali. Alla seconda armonica corrispondono fotoni di energia:

DE = 2hw - 2(2n + 3) x_e hw - ...              n + 2 ? n

La comparsa di righe che traggono origine da livelli differenti è utile al calcolo di x_e e di D_e .

Spettri vibrorotazionali

Ogni linea di uno spettro vibrazionale di una molecola biatomica eteronucleare, effettuato ad alta risoluzione, consiste di un gran numero di righe strettamente intervallate. E’ per questo motivo che gli spettri molecolari sono chiamati spettri di bande (vedi figura in basso) mentre quelli atomici sono chiamati spettri di righe.

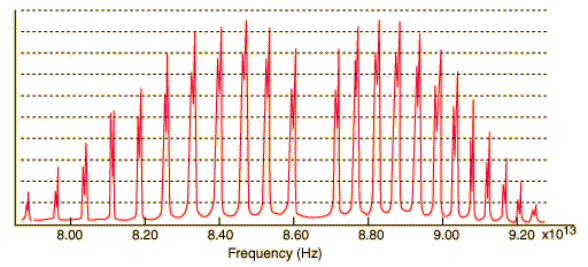Gli intervalli fra le righe di una stessa banda sono dell’ordine di qualche cm^-1, e questo significa che tale struttura sia dovuta a transizioni rotazionali contemporanee alla transizione vibrazionale. Infatti la quantità di energia che entra in gioco nella transizione vibrazionale è talmente grande da eccitare i livelli rotazionali molecolari.

Inoltre la variazione vibrazionale è assimilabile a un mutamento transitorio del momento d’inerzia, al quale la molecola risponde con il mutamento del proprio stato rotazionale ed in particolare variando la frequenza del moto rotatorio per mantenere costante il valore del momento angolare totale della molecola. Per il principio di conservazione del momento angolare J = Iw, ad una diminuzione del momento d’inerzia deve corrispondere un aumento della frequenza angolare.

L’indagine particolareggiata dimostra che la regola di selezione per la variazione rotazionale associata al mutamento vibrazionale è ancora:

DJ = ± 1

eccetto che in circostanze particolari, come nel caso della molecola di monossido di azoto (NO), in cui si registra un momento angolare elettronico intorno all’asse della molecola lineare e la conservazione del momento angolare a tale sistema, può essere soddisfatta anche dalla condizione DJ = 0.

La figura a lato mostra la suddivisione dei livelli energetici molecolari, come si vede fra uno stato vibrazionale e l’altro esistono diversi stati rotazionale spaziati da distanze molto minori rispetto quelli vibrazionali. Di conseguenza l’espressione dei livelli energetici di una molecola soggetta a vibrazione e rotazione, tenuto anche conto del fattore di anarmonicità, risulta:

E(J,n) = BJ(J+1) + (n + ½) hw – (n + ½)² x_e hw

Si noti che la costante rotazionale B è la stessa per tutti i valori sia di J che di n, la separazione fra due livelli di un dato J è la stessa sia nello stato n = 0 che in quello n = 1.

Un’analisi dettagliata della meccanica quantistica sui cambiamenti simultanei nelle rotazioni e vibrazioni di una molecola, mostra che il numero quantico rotazionale J cambia di ± 1 durante la transizione vibrazionale delle molecole biatomiche. La regola di selezione vibrazionale è:

D n = ± 1 ± 2 ± 3

Quando si verifica una transizione vibrazionale non solamente n passa ad n + 1 (nell’assorbimento), ma J cambia di 0 (non cambia) o di ± 1, tale variazione dipende dalle molecole considerate.

La frequenza

n₀ = n (1 - 2 x_e)

è chiamata origine o centro di banda; essa individua la regione centrale della riga di assorbimento vibrazionale, la quale risulta suddivisa in tre insiemi di righe detti rami contrassegnati da tre diverse lettere in base al valore assunto da DJ.

Tale situazione è illustrata nella figura seguente dalla quale si evince inequivocabilmente la contemporanea eccitazione dei livelli rotazionali durante una transizione vibrazionale. Come si vede appunto dalla figura, per ogni livello vibrazionale esistono nove livelli rotazionali permessi.

Passiamo ora ad una piccola ma importante descrizione dei tre rami in cui è divisa la riga spettrale vibrazionale:

Ramo P: Tali righe corrispondono a transizioni per le quali valgono D n =  1 e DJ = -1. Quindi se la 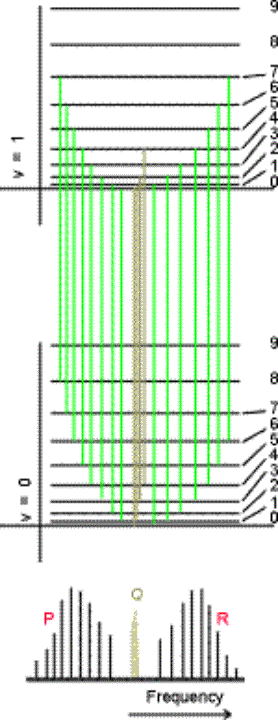molecola si trovava inizialmente nello stato J, la transizione è J  ®  J = -1 e il cambiamento totale di energia che determina anche il valore delle frequenze di tali righe è (basta dividere per h):

DE = hw - 2BJ

Ciò rende conto delle righe che cadono alla sinistra del centro di banda aventi delle frequenze inferiori coincidenti con: w – 2B,  w – 4B,…

Ramo Q: Le righe di tale ramo prendono origine dalle transizioni con D n =  1 e DJ = 0. Le loro frequenze sono date dal valore energetico:

DE = hw

per tutti i valori di J. Il ramo Q, quando è permesso, è una sola riga alla frequenza di centro banda, ma nelle molecola reali, poiché le costanti rotazionali sono diverse per i diversi livelli vibrazionali, tale ramo risulta dall’addensarsi di un gruppo di righe strettissimamente intervallate (come si evince dalla figura qui a lato).

Ramo R: Risulta composto dalle righe le cui frequenze corrispondono alle transizioni con D n =  1 e DJ = 1 e si calcolano facilmente dalla seguente e relativa espressione dei livelli energetici:

DE = hw + 2B(J + 1)

Le righe sono spostate di 2B, 4B,… verso le alte frequenze rispetto alla fondamentale (frequenza di centro banda).

Dall’intervallo fra le righe P ed R di una transizione vibrazionale, si ricava il valore di B e da questo la lunghezza del legame senza bisogno di ricorrere allo spettro a microonde, rotazionale puro, anche se con quest’ultimo si ottengono risultati di una maggiore precisione.

Spettroscopia Raman

Nella spettroscopia Raman i livelli energetici della molecola sono “esplorati” analizzando le frequenze presenti nella radiazione scatterata (diffusa) dalla molecola. In un tipico esperimento Raman, un fascio di luce monocromatica viene fatto incidere sul campione per poi rilevarne la 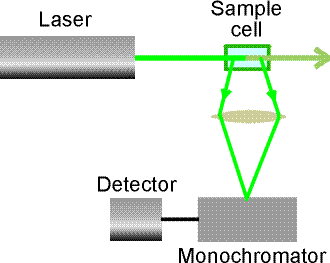radiazione diffusa ad un angolo ortogonale rispetto alla direzione del fascio incidente (vedi figura). Quando i fotoni incidenti urtano la molecola, essi possono perdere o guadagnare energia: se la molecola assorbe parte dell’energia del fotone per passare ad uno stato eccitato, il fotone riemergerà con un’energia (frequenza) minore di quella d’incidenza andando a formare le cosiddette righe Stokes dello spettro Raman; se invece la molecola si trova già in uno stato eccitato (l‘energia termica a temperatura ambiente eccita alcuni stati rotazionali) può cedere energia al fotone incidente che riemergerà dall’urto con un’energia maggiore andando a formare le righe anti-Stokes.

La componente della radiazione diffusa nella stessa direzione d’origine senza cambiamenti di frequenza è chiamata radiazione Rayleigh.

Gli spostamenti in frequenza della radiazione diffusa dalla radiazione incidente sono molto piccoli e di conseguenza la radiazione incidente deve essere “molto monocromatica” per poter osservare gli spostamenti in frequenza. Inoltre l’intensità della radiazione diffusa è molto bassa quindi è necessario che il fascio incidente sia anche molto intenso. I Laser sono delle sorgenti di radiazioni elettromagnetiche perfetti per tali esperimenti. I primi spettri Raman compiuti con un laser vennero esaminati usando luce incidente con frequenze nel visibile e nell’ultravioletto, oggi la radiazione incidente cade nel vicino infrarosso per evitare complicazioni scaturenti dalla stimolazione della fluorescenza. La rivelazione della radiazione Raman è effettuata di solito mediante dei detector a semiconduttore; essa risulta complementare alla spettroscopia infrarosso perché , come vedremo fra poco, obbedisce a diverse regole di selezione e vengono osservate diverse transizioni.

Spettri Raman rotazionali

La più importante regola di selezione per le transizioni Raman rotazionali è che la molecola abbia una polarizzabilità anisotropa: una molecola quando è immersa in un campo elettrico viene distorta (subisce una polarizzazione per deformazione) a causa delle forze elettriche agenti sui nuclei in un senso e sugli elettroni in senso opposto. L’intensità di tale deformazione dipende dalle caratteristiche fisico-chimiche della molecola rappresentate in tal senso da una grandezza che prende il nome appunto di polarizzabilità elettrica (a). Una polarizzabilità elevata porta la molecola a essere deformata anche da un campo elettrico esterno di lieve intensità. Per esempio è più facile deformare un atomo di Xenon, i cui elettroni esterni sono legati meno fortemente al nucleo, rispetto ad un atomo di Elio i cui unici due elettroni sono legati fortemente al nucleo; di conseguenza diremo che lo Xenon ha una polarizzabiltà più elevata dell’Elio.

Più precisamente, se l’intensità del campo elettrico esterno applicato è E allora la molecola acquisisce un momento di dipolo indotto la cui ampiezza (o modulo) risulta:

che va ad aggiungersi a ogni momento di dipolo permanente che abbia o meno la molecola. Un atomo è polarizzabile isotropicamente poiché qualunque sia la direzione del campo elettrico applicato, è indotta la stessa deformazione della nuvola elettronica. Per le molecole questo non è valido ad esclusione ovvia dei rotori sferici, infatti le molecole non sferiche hanno una polarizzabilità che dipende dalla direzione del campo applicato alla molecola. Quindi tali molecole sono 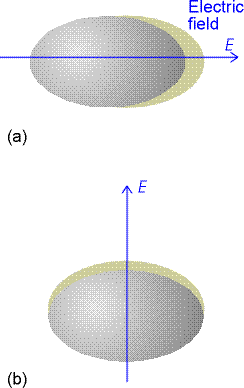contraddistinte da avere una polarizzabilità anisotropa. Per esempio, come si vede nella figura, la distribuzione elettronica della molecola d’idrogeno (H₂) è più deformata quando il campo elettrico è applicato parallelamente alla congiungente i nuclei (direzione del legame) rispetto alla direzione ad essa ortogonale, quindi avremo in tal caso:

Tutte le molecole lineari e biatomiche, sia omo che eteronucleari, hanno una polarizzabilità anisotropa e quindi sono rotazionalmente raman attive.Questa è una delle  ragioni dell’importanza della spettroscopia raman, poiché tale tecnica può essere usata per studiare la struttura rotazionale di molecole inaccessibile alla spettroscopia delle microonde (puri spettri rotazionali). Infatti la spettroscopia Raman può essere usata per studiare la struttura rotazionale di molecole non possedenti un momento di dipolo permanente e quindi non mostrando uno spettro rotazionale nella regione delle microonde.

Regole di selezione per le transizioni Raman

Negli spettri Raman rotazionali le regole di selezione specifica sono:

Rotori lineari: D J = 0, ± 2

Rotori simmetrici: D J = 0, ± 1, ± 2: D K = 0

La presenza della cifra 2, quella più significativa, si può ricondurre al fatto che ad ogni rivoluzione 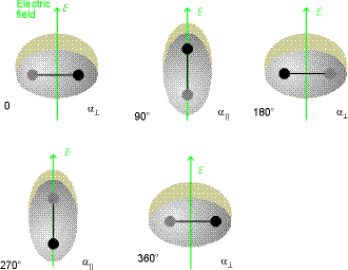la polarizzabilità della molecola riacquista il valore iniziale due volte (vedi figura a lato); considerando il momento di dipolo sembra che la molecola ruoti a velocità doppia. Inoltre considerando la conservazione del momento angolare e che lo spin fotonico ha valore unitario, tale cifra resta giustificata dal fatto che nel processo Raman entrano in gioco due fotoni, uno incidente e l’altro emergente.

Classicamente il requisito della polarizzabilità anisotropa e della presenza del fattore 2 è legata al fatto che se si irradia una molecola con una luce di frequenza w_i, il momento di dipolo indotto nella molecola dipende dall’ampiezza del campo elettrico applicato:

Se la molecola ruota con frequenza angolare di rotazione w_R, allora per un osservatore esterno la sua polarizzabilità dipende anche dal tempo (se è appunto anisotropa) e coincide con:

dove a₀ rappresenta la polarizzabilità media,  e a varia da a _o + D a a a _o - D a mentre la molecola ruota. Sostituendo l’espressione della polarizzabilità nell’espressione del momento di dipolo indotto ed eseguendo alcune relazioni trigonometriche, otteniamo:

Questi calcoli mostrano che il momento di dipolo indotto ha una componente oscillante alla stessa frequenza della radiazione incidente, questa componente come detto genera la componente Rayleigh. Il momento ha inoltre due componenti oscillanti a w_i + 2w_R che danno la spiegazione delle “spostate” righe Raman: il segno meno corrisponde alle righe Stokes, il segno più alle righe 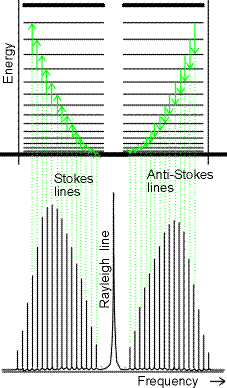anti-Stokes (vedi figura a lato). E’ importante notare come tali linee appaiono solamente se D a ? 0 e cioè che la polarizzabilità sia appunto anisotropa.

Quando la molecola subisce una transizione con D J = + 2 la luce diffusa lascia la molecola in uno stato rotazionale superiore (eccitato) e quindi ne emerge con frequenza (energia) diminuita. Tale transizione spiega la presenza delle righe Stokes dello spettro raman; la frequenza corrispondente può essere ricavata, conoscendo i livelli energetici molecolari, dalla seguente espressione:

Righe Stokes (D J = + 2):                 n = n₀ – 2B(2J + 3)               per    J   ®  J + 2

Tali righe compaiono sul lato di minore frequenza rispetto a quella della luce incidente n₀, e con spostamenti 6B, 10B,14B,… In corrispondenza di stati ad elevato valore di J, l’intensità delle righe si attenua poiché sono stati scarsamente popolati.

Quando invece la molecola, collidendo con il fotone incidente, subisce la transizione D J = - 2, il fotone acquisisce l’energia eccedente e riemerge con una frequenza superiore andando a formare le righe anti-Stokes, la cui determinazione in frequenza è data da:

Righe anti-Stokes (D J = - 2):               n = n₀ + 2B(2J – 1)               per    J   ®  J – 2

Gli spostamenti in tale caso sono sul lato delle frequenze superiori rispetto a quella della luce incidente e valgono 6B, 10B, 14B,…

Dall’analisi dello spettro rotazionale Raman, ed in particolare dalla misura della spaziatura fra le righe, si ricavano informazioni riguardanti il momento d’inerzia (calcolato dal valore di B) della molecola perpendicolare all’asse di simmetria della stessa molecola e da questa misura i dati riguardanti il legame esistente nella molecola.

Spettri Raman vibrazionali

La regola di selezione generale per la comparsa dello spettro Raman vibrazionale si basa sulla variabilità della polarizzazione elettrica molecolare. Solo se la vibrazione della molecola implica una variazione della polarizzabilità, tale vibrazione molecolare è attiva nel Raman.

Il “solito” fotone incidente può dar luogo a scambi d’energia se l’urto con la molecola provoca una eccitazione (diminuzione della frequenza del fotone incidente) o diseccitazione (aumento della frequenza del fotone) vibrazionale della molecola con conseguente variazione della polarizzabilità. La regola di selezione specifica è:

D n = ± 1

Le righe che compaiono a frequenze superiori rispetto la radiazione incidente, sono le anti-Stokes e corrispondono a D n = - 1. Si tratta di righe molto poco intense a causa della scarsa popolazione di livelli vibrazionali eccitati. Le righe che si trovano sul lato delle frequenze minori sono le Stokes, accompagnate da transizioni D n = + 1. Ad entrambi gruppi di righe si sovrappongono come nel caso della spettroscopia infrarossa, la struttura ramificata derivante dalle transizioni rotazionali in seno a quelle vibrazionali.

Per tali transizioni rotazionali vale la regola di selezione D J = 0 o D J = ± 2, come per gli spettri Raman rotazionali puri. I rami corrispondenti si dicono ramo O per D J = - 2, ramo Q per D J = 0 quando è permesso, e ramo S per D J = + 2.

Tale struttura è in totale analogia agli spettri vibrorotazionali puri (mostrati in figura a pagina 15); spettri ottenuti dall’assorbimento o dall’emissione di fotoni da parte della molecola, mentre nella spettroscopia Raman si analizza la radiazione diffusa dagli urti dei fotoni incidenti con la molecola in esame. In particolare la spettroscopia Raman offre la possibilità di studiare le molecole biatomiche omonucleari (non dotate di momento di dipolo permanente) ricavando dalla spaziatura fra le righe Stokes (le anti-Stokes sono come detto troppo poco intense) la loro costante di forza misurante la rigidità della molecola. Inoltre è possibile interpretare la struttura rotazionale degli spettri in funzione delle costanti rotazionali delle molecole per poter stabilire la lunghezza dei legami ecc.

Per le molecole poliatomiche esistono dei modi vibrazionali attivi nel Raman ed altri no.  La regola di esclusione afferma che se la molecola possiede un centro di simmetria (il centro di simmetria delle cariche positive coincide con quello delle cariche negative = molecole apolari), allora i suoi modi che risultano inattivi nell’infrarosso sono attivi nel Raman e viceversa.

Questa regola vale per l’anidride carbonica (CO₂) ma non per l’acqua (H₂O) mancando in tale molecola il centro di simmetria. In definitiva per avere tutti i dati relativi alla rigidità (campo di forze) di una molecola, è necessario servirsi tanto dello spettro I.R. quanto del Raman.