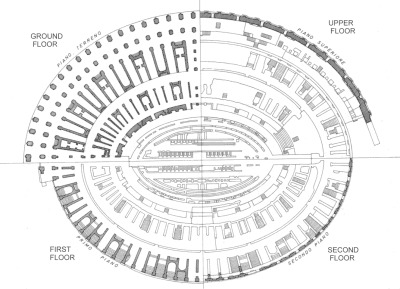
ELLIPSIS ?

The arena (and the whole Colosseum) is supposed to be elliptical, but the curve of the arena, which has now been measured to a high degree of accuracy, does not coincide exactly with an ellipse. So, the scholars who have studied the problem in modern times have hypotized that the curve of the arena is a polycentric one, i.e. a curve designed by calculating the different centres of the curves by means of a geometric system.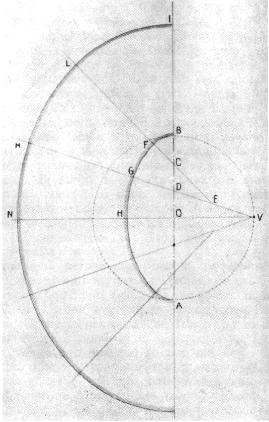

This was the system, according to Ingegner Giuseppe Cozzo: AB is the length of the arena, and BI is a constant measure, corresponding to the width of the building. Draw a circle of centre O and of radius OB (half of the length) and divide the segment OB into three equal parts (BC=CD=DO). The line VM starts from the extreme V of the quadrant BOV, intersecting D.

Divide in 2 parts the line segment VD and find E. Draw the line EL intersecting C. Then draw the sector FB by centering the circle in C (of radius BC), draw the sector FG by centering the circle in E (of radius EF), and finally the sector GH by centering the circle in V (radius VG). Add the BI constant to the curves, so as to obtain the measures HN, GM, FL which give the perimeter of the building. Repeat this procedure for the other three quadrants of the amphitheatre. Done.

According to Cozzo, the small differences between the ideal curve and the reality of the amphitheatres should account on little errors made originally by the architect, or by errors made by us when measuring dilapidated monuments.

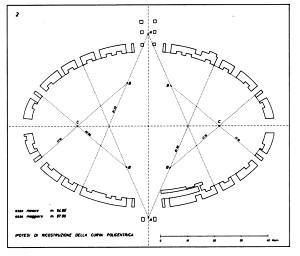
In a more recent study, Professor Camillo Trevisan has advanced different hypothesis on the geometric system(s) used. By more accurate measurements, he noticed that there are small differences between the hypothetical curve as described by Cozzo and the real measures of the amphitheatres, and presents an explanation

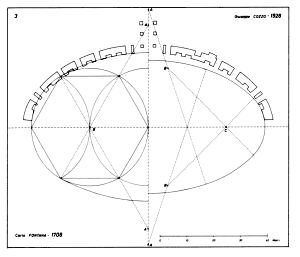
A reconstruction by G. Cozzo comparing the curve of Fontana (left) and his (right)	Another reconstruction of the curve