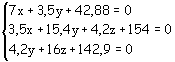
La risoluzione dei sistemi lineari di equazioni con il metodo di Leibniz – Cramer.
Problema. Risolvere il seguente sistema utilizzando il metodo di Leibniz-Cramer.
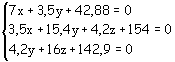
Come prima operazione si ordinano le equazioni, incolonnando opportunamente le incognite e spostando alla destra del segno di uguale il termine noto; se non è presente un'incognita, la si aggiunge moltiplicandola per il coefficiente zero.
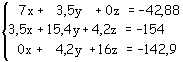
Con i coefficienti delle incognite si forma il determinante
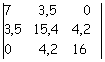
Con i termini noti si forma il vettore
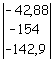
Secondo Leibniz (Gottfried Wilhelm von, 1646-1716 filosofo e scienziato tedesco) e Cramer (Gabriel, 1704-52 matematico svizzero) la soluzione del sistema è fornito dai seguenti rapporti di determinanti
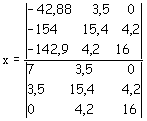
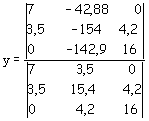
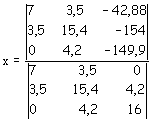
Il determinante al denominatore è costituito dai coefficienti dei termini noti
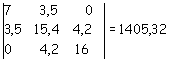
Il determinante per il calcolo della x è ottenuto sostituendo la colonna dei coefficienti della x con il vettore dei termini noti.
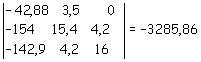
Il determinante per il calcolo della y è ottenuto sostituendo la colonna dei coefficienti della y con il vettore dei termini noti.
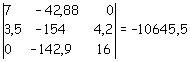
Il determinante per il calcolo della z è ottenuto sostituendo la colonna dei coefficienti della z con il vettore dei termini noti
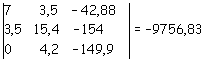
In definitiva si ottiene
![]()
![]()
![]()
Il calcolo con Excel.![]()
|
|
Inserimento dei dati. A partire dalla cella R2C1 si inseriscono i valori dei coefficienti e dei termini noti. Per maggiore chiarezza vengono colorate in giallo le celle con i valori dei coefficienti e in verde quelle contenenti i valori dei termini noti. Costruzione del determinante dei coefficienti. Nella cella R7C1 si digita il simbolo = e si punta con il mouse nella cella R2C1, concludendo, infine, con la pressione del tasto Invio. Si copia a destra la cella R7C1 trascinando di due posizioni il quadratino in basso a destra. Si copiano in basso di due posizioni le celle da R7C1 a R7C3. |
|
|
Calcolo del determinante. Dopo essersi posizionati nella cella R7C4 si fa clic sul pulsante per l''inserimento delle funzioni di Excel
Dalla finestra di dialogo Incolla funzione si sceglie la categoria Matematiche e trig. e il Nome funzione MATR.DETERM. Come argomento della funzione si inserisce il rettangolo di celle da R7C1 a R9C3. La formula risultante è =MATR.DETERM(RC[-3]:R[2]C[-1]) |
Costruzione del determinante x.
Si ripete il procedimento già seguito per la creazione del determinante dei coefficienti, partendo questa volta dalla cella R7C6. Per sostituire la prima colonna del determinante con quella dei termini noti si digita il simbolo = nella cella R7C6, si fa clic sulla cella R2C4 ed, infine si batte Invio; la formula così ottenuta viene ricopiata in basso di due righe.
Il valore del determinante x si calcola con la stessa procedura già esaminata a proposito del calcolo del determinante dei coefficienti.
Costruzione dei determinanti y e z.
Si ripete il procedimento seguito per il determinante x apportando la seguente variazione: le colonne dei coefficienti da sostituire con quella dei termini noti sono quelle relative alle y e alle z.
Calcolo dell'incognita x.
Nella cella R2C7 si digita il simbolo = , si fa clic sulla cella R7C9, si inserisce il simbolo /, si fa clic sulla cella R7C4 ed infine si batte Invio.
La formula risultante è R[5]C[2]/R[5]C[-3]
Calcolo delle incognite y e z.
Si ripete il procedimento già visto per l'incognita x partendo dalle celle R8C9 e R10C9 ed inserendo il valore dei rispettivi determinanti y e z nella formula.
|
|
Perché il sistema sia risolvibile le equazioni devono essere tra di loro indipendenti; se ciò non si verifica, il valore del determinante dei coefficienti è nullo. Poiché tale determinante è inserito al denominatore nelle formule per il calcolo delle incognite conduce ad un errore. E' opportuno perciò l'inserimento di un controllo che evidenzi un messaggio nel caso il sistema non sia risolvibile; questo obiettivo può essere raggiunto mediante l'uso della funzione SE(). In altri termini: se il valore del determinante dei coefficienti è diverso da zero, si calcola il valore dell'incognita altrimenti si visualizza un messaggio del tipo "equazioni linearmente dipendenti". La formula per il calcolo della x può essere così riscritta =SE(R[5]C[-3]<>0;R[5]C[2]/R[5]C[-3];"eq. linearm. dipendenti") |
|
Argomenti correlati | |
|
La risoluzione dei sistemi lineari (forma matriciale) con Excel |
|