|
|
 |
Classi laterali modulo un
sottogruppo e teorema di Lagrange |
 |
|
|
Proposizione |
Sia dato
un gruppo G e un suo sottogruppo S. Le relazioni su G definite
da |
"a,b╬G a rd b  ab
-1╬S ab
-1╬S |
"a,b╬G a rs b  b -1a ╬S b -1a ╬S |
sono
relazioni di equivalenza |
|
Dim. |
a rd a  aa -1╬S aa -1╬S  u╬S , ma questo Ŕ
vero dato che S<G u╬S , ma questo Ŕ
vero dato che S<G |
ard b  ab -1╬S , ma S<G
e quindi (ab -1) -1= ba -1╬S ab -1╬S , ma S<G
e quindi (ab -1) -1= ba -1╬S  b rd a b rd a |
ard b e brd c  ab
-1, bc -1╬S ab
-1, bc -1╬S  ab -1bc
-1╬S ab -1bc
-1╬S  ac -1╬S ac -1╬S  a rd c a rd c |
Analogamente per
l'altra relazione. |
|
Osservazione |
Se si
utilizza la notazione additiva (G, +), le relazioni si scriveranno |
"a,b╬G a rd b  a-b╬S a-b╬S |
"a,b╬G a rs b  -b+a╬S -b+a╬S |
Nel
seguito utilizzeremo la notazione moltiplicativa. |
Se il
gruppo Ŕ commutativo, "a,b╬G ab -1= b -1a e quindi le due relazioni coincidono: rd = rs |
Se il
gruppo non Ŕ commutativo, possiamo dare esempi in cui le due relazioni non coincidono... |
|
|
Come sempre
quando si ha una relazione di equivalenza su un insieme, bisogna vedere come sono fatte le
sue classi di equivalenza: |
[a]rd = { x╬G / x rd
a }= { x╬G / xa -1╬S
}= { x╬G / $s╬S:
xa -1= s}={ x╬G / $s╬S: x = sa} |
[a]rs = { y╬G / y rs
a }= { y╬G / a -1y╬S
}= { y╬G / $s╬S:
a -1y=
s}={ y╬G / $s╬S:
y = as} |
Abbiamo dimostrato la seguente proposizione: |
Proposizione |
Sia dato
un gruppo G e un suo sottogruppo S. Le classi di equivalenza delle
relazioni di equivalenza su G definite da |
"a,b╬G a rd b  ab
-1╬S ab
-1╬S |
"a,b╬G
a rs b  b -1a ╬S b -1a ╬S |
sono: |
|
|
[a]rd = { x╬G / $s╬S:
x = sa} =
{sa, s╬S } |
[a]rs= { y╬G / $s╬S:
y = as} =
{as, s╬S } |
|
La classe di equivalenza [a]rd Ŕ l'insieme dei prodotti sa con s╬S , i suoi elementi si ottengono quindi moltiplicando a destra per a.
|
La classe di equivalenza [a]rs Ŕ l'insieme dei prodotti as con s╬S , i suoi elementi si ottengono quindi moltiplicando a sinistra per a.
|
Ci˛ giustifica la seguente definizione e la notazione utilizzata per
indicare le relazioni di equivalenza: |
|
Definizione |
Sia dato un gruppo G e un suo sottogruppo S. |
Dato a╬G, si
definisce classe laterale destra dell'elemento a modulo il sottogruppo S, e
si indica con Sa, il sottoinsieme di G |
Sa = { x╬G / $s╬S:
x = sa} =
{sa, s╬S } |
Dato a╬G, si
definisce classe laterale sinistra dell'elemento a modulo il sottogruppo S, e
si indica con aS, il sottoinsieme di G |
aS = { x╬G / $s╬S: x = as} = {as, s╬S } |
Con
questa definizione si ha dunque |
[a]rd = Sa |
[a]rs = aS |
La
relazione di equivalenza su G definita da |
"a,b╬G a rd b  ab
-1╬S ab
-1╬S |
| si dice congruenza destra modulo S |
La
relazione di equivalenza su G definita da |
"a,b╬G a rs b  b -1a╬S b -1a╬S |
si dice congruenza sinistra modulo S |
|
|
Tra gli
elementi di G, c'Ŕ l'elemento neutro u. Siamo curiosi di sapere
chi sono [u]rd e [u]rs.
Risulta |
[u]rd = Su =
S |
[u]rs = uS =
S |
Le classi laterali (destre o sinistre) sono sottoinsiemi di G in
generale non sottogruppi, ma [u] = S Ŕ un sottogruppo ed Ŕ anzi l'unica delle
classi laterali che Ŕ anche sottottogruppo di G. |
|
Quaalcuno
potrebbe obiettare che si sarebbero potute definire altre due relazioni sulla falsa riga
delle precedenti: |
"a,b╬G
a t b  a -1b╬S a -1b╬S |
"a,b╬G a u
b  b a-1╬S b a-1╬S |
In realtÓ non si ottiene nulla di nuovo: |
[a]t = { x╬G
/ a
t x }= { x╬G / a -1xXS }= { x╬G / $s╬S: a -1x = s}={ x╬G / $s╬S: x = as}= aS = [a]rs |
[a]u = { x╬G
/ a
u x }= { x╬G / xa -1╬S }= { x╬G / $s╬S: xa
-1= s}={ y╬G / $s╬S: x = sa}= S a = [a]rd |
e quindi t = rs e u = rd |
|
Esempio |
Considerato il
gruppo D4 ={id,
r, r
2, r
3, t,
t ░r,
t ░r 2, t ░r
3} e il suo sottogruppo S ={id,
r 2},
determiniamo le classi laterali destre e sinistre degli elementi di D4
modulo S: |
| idS = S = r 2S |
|
|
Sid = S = Sr 2 |
|
| rS = {r, r 3} = r 3S |
|
|
Sr = {r, r 3} = Sr 3 |
|
| tS = {t, t ░r 2}
= (t ░r 2)S |
|
|
St = {t, t ░r 2}
= S(t
░r 2) |
|
| (t ░r)S = {t ░r
, t ░r 3}
= (t ░r 3)S |
|
|
S(t ░r) = {t ░r
, t ░r 3}
= S(t
░r 3) |
|
|
|
|
|
|
|
Notiamo che
risulta aS = Sa "a╬D4 , ma ci˛ non Ŕ vero in generale. |
Considerato
infatti il sottogruppo T ={id,
t}. si ha |
| idT = T = tT |
|
Tid = T = Tt |
| rT = {r, t ░r 3}
= (t ░r 3)T |
|
Tr = {r, t ░r } = (t ░r )T |
| r 2T
= {r
2, t ░r 2}
= (t ░r 2)T |
|
Tr
2 = {r 2, t ░r
2} = (t ░r 2)T |
| r 3T
= {r
3, t ░r } = (t ░r )T |
|
Tr
3 = {r 3, t ░r
3} = (t ░r 3)T |
|
|
|
|
Questa volta si
ha rT ╣Tr e r
3T
╣Tr
3. Scopriremo in seguito perchŔ si ha questa differenza
e l'importanza del caso ... |
|
Proposizione |
Sia dato
un gruppo G e un suo sottogruppo S, allora "a╬G risulta |
aS = Sa  aSa -1 =
S aSa -1 =
S |
Dim. |
aS = Sa
 (aS)a -1 =
(Sa)a -1 (aS)a -1 =
(Sa)a -1
 aSa -1= S aSa -1= S |
|
Proposizione |
Sia dato
un gruppo G e un suo sottogruppo S. Le classi laterali (destre o
sinistre) modulo S hanno la stessa cardinalitÓ di S: |
| aS | = | S | "a╬G |
| Sa | = | S | "a╬G |
e di
conseguenza tutte le classi laterali hanno la stessa cardinalitÓ. In particolare |
| aS | = | Sa | "a╬G |
| aS | = | bS | "a,b╬G |
Dim. |
Dimostriamo
solamente che | aS | = |
S | "a╬G |
Una biiezione tra
S e aS Ŕ, ad esempio, |
|
|
La funzione Ŕ
iniettiva: as = as'  s
= s' s
= s' |
La funzione Ŕ suriettiva: as = ja(s) |
|
Riportiamo in
un'unica proposizione le proprietÓ finora viste delle classi laterali |
Proposizione |
Dato un
gruppo G e un suo sottogruppo S, "a,b╬G risulta |
aS =
bS  a -1b╬S a -1b╬S
|
Sa = Sb  a
b-1╬S a
b-1╬S
|
aS =
S  a╬S a╬S
|
Sa = S  a╬S a╬S
|
|
|
|
|
|
|
|
|
|
aS < G  a╬S a╬S
|
Sa < G  a╬S a╬S
|
aS =
Sa  aSa -1 =
S aSa -1 =
S
|
|
|
Le classi laterali (destre o sinistre) costituiscono una partizione di G
e quindi possiamo considerare gli insiemi quozienti |
G /rd = {Sa , a╬G} |
G /rs = {aS , a╬G} |
Proposizione |
Sia dato
un gruppo G e un suo sottogruppo S. Gli insiemi quozienti G/rd e G/rs hanno la stessa
cardinalitÓ |
| G/rd | = | G/rs | |
Dim. |
Una biiezione tra G/rd ={Sa , a╬G} e G/rs ={aS , a╬G}Ŕ,
ad esempio, |
| j
: |
G/rd |
« |
G/rs |
|
Sa |
« |
a
-1S |
|
|
|
|
|
Attenzione! Se avete accettato questa definizione di funzione senza
battere ciglio, dovreste preoccuparvi. Ricordate
sempre che quando una funzione ha come dominio un insieme quoziente e il valore
corrispondente a una classe viene assegnato tramite un rappresentante dovete verificare
che la definizione Ŕ ben posta, ossia che Ŕ indipendente dal rappresentante scelto,
altrimenti non Ŕ nemmeno una funzione. |
La funzione Ŕ ben definita: Sa = Sb  ab
-1╬S ab
-1╬S
 b -1╬ a -1S b -1╬ a -1S  a -1S
= b -1S a -1S
= b -1S |
La funzione Ŕ iniettiva: a -1S
= b -1S  b
-1╬
a -1S b
-1╬
a -1S  ab -1╬S ab -1╬S  Sa = Sb Sa = Sb |
La funzione Ŕ suriettiva: a -1S = j(Sa) |
|
|
Definizione |
Sia dato
un gruppo G e un suo sottogruppo S. La cardinalitÓ dell'insieme
quoziente G/rd ( G/rs ) si chiama
indice di S in G e si indica con [G : S] |
[G : S ] = |
G/rd
| =|{Sa , a╬G}| |
[G : S ] = |
G/rs
| =|{aS , a╬G}| |
|
|
Teorema (Lagrange) |
Dato un
gruppo finito G e un suo sottogruppo S,
risulta |
| G | = [G : S ] | S
| |
e quindi
la cardinalitÓ di S divide la cardinalitÓ di G (e anche l'indice di S
in G divide la cardinalitÓ di G ). |
Dim. |
Osserviamo
innanzitutto che nel caso di un gruppo G finito anche S<G
Ŕ finito e [G : S ] Ŕ il numero di classi
laterali destre (sinistre). Siccome le classi laterali destre costituiscono una partizione
di G, si ha |
|
|
|
|
|
|
G = |
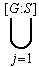 |
Saj |
|
|
|
|
|
|
|
ed, essendo l'unione disgiunta, |
|
|
|
|
|
|
| G | = |
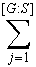 |
| Saj| |
|
|
|
|
|
|
|
ma | Saj| =| S | e quindi |
|
|
|
|
|
|
| G | = |
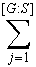 |
| S | |
=[G : S ] | S
| |
|
|
|
|
|
|
|
Esempio |
|
|
|
|
|