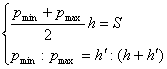TEORIA DI COULOMB

Terrapieno senza sovraccarico

Terrapieno con sovraccarico uniforme

I moderni metodi di calcolo della spinta delle terre si basano sulla conoscenza della vecchia teoria, divenuta classica, proposta da Coulomb già nella seconda metà del 18° secolo.

Ricordiamo che per spinta delle terre s’intende la risultante delle pressioni esercitata da un prisma di terra contro un’opera di sostegno. L’angolo formato dalla scarpa di un volume di terra, naturalmente stabile, rispetto ad un piano orizzontale è definito angolo d’attrito interno j. Tutte le superfici inclinate sull’orizzontale di un angolo a>j costituiscono probabili piani di scorrimento del volume di terra sovrastante, che può scivolare a valle. Per impedire che ciò accada è necessario sostenere la terra franante con opere capaci di riportare l’equilibrio: tali opere sono i muri di sostegno.

La teoria di Coulomb si basa sulle seguenti ipotesi fondamentali:

1. il volume di terra è incoerente e privo di coesione, che è una forza di adesione tra le particelle di terra dipendente dalle loro proprietà chimiche e granulometriche;

2. si trascura l’attrito tra terra e paramento interno del muro;

3. la superficie di scorrimento del prisma di terra è piana;

4. il terrapieno è orizzontale e il paramento interno del muro è verticale;

5. il muro subisce un congruo cedimento in avanti, dell’ordine di h/2000.

È necessario, ora, considerare fisicamente l’evolversi del fenomeno di franamento del prisma di terra. Il muro, non appena "avverte" la spinta della terra, definita spinta iniziale o di quiete S₀, compie un piccolo cedimento in avanti di traslazione o di rotazione e, durante tale cedimento, anche il prisma di terra che sta a monte della parete è soggetto ad un movimento di assestamento. Terminato il cedimento, il muro è soggetto ad una nuova spinta, definita spinta attiva S_a, che rappresenta la spinta che il muro deve contrastare attivamente nella situazione di stabilità. La spinta attiva S_a, chiamata anche spinta coulombiana, è nettamente minore (circa il 50%) della spinta iniziale S₀, in quanto quest’ultima deve "spendere" parte della propria energia per vincere le resistenze d’attrito, che si sviluppano lungo la superficie di scorrimento durante il cedimento. Per quanto detto si consiglia di non sovradimensionare i muri di sostegno altrimenti, essendo molto rigidi e non permettendo quindi alcun cedimento, essi rimangono soggetti alla spinta iniziale S₀ che, come appena detto, è molto maggiore della spinta attiva S_a.

Spinta di Coulomb in un terrapieno senza sovraccarico

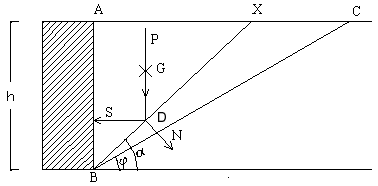
Sulla base di queste ipotesi, al fine di determinare la spinta, Coulomb prende in esame un terrapieno con superficie orizzontale che grava su un muro con paramento interno verticale. Si traccia il piano di declivio naturale AC, inclinato dell’angolo j rispetto all’orizzontale, poi si considera un generico prisma di terra racchiuso tra il paramento del muro ed il piano di scorrimento BX inclinato di un angolo a>j, il tutto per una profondità di muro pari a 1 metro.

Terrapieno orizzontale senza sovraccarico

 Il peso P del prisma di terra di traccia ABX, applicato nel baricentro G, vale:

in cui

e quindi

Supponendo che il muro non abbia ancora subito il congruo cedimento (istante iniziale), il vettore P incontra il piano di scorrimento BX nel punto D, in cui può essere scomposto in una componente S₀, perpendicolare al paramento del muro, e in una componente N, perpendicolare al piano di scorrimento BX:

- la componente S₀ rappresenta la spinta di quiete, prima del congruo cedimento, perpendicolare alla parete in quanto, come detto nelle ipotesi, non si considera l’attrito tra terra e paramento del muro;

- la componente N è la pressione che agisce sul terreno sottostante, il quale reagisce con un vettore –N.

Rappresentiamo il vettore P con il segmento 0-1, e lo scomponiamo nel vettore S e nel vettore N, rappresentati rispettivamente dai segmenti 0-2 e 2-1.

determinazione grafica della spinta di quiete S0 e della spinta attiva Sa

La spinta di quiete S₀, rappresentato dal segmento 0-2, vale

Appena avviene il cedimento del muro per effetto della spinta S₀, il prisma di terra ABX scivola lungo il piano BX e qui, a causa del movimento, si sviluppano resistenze d’attrito che valgono:

Questo perché, ricordando dalla Fisica il comportamento di un corpo su un piano inclinato:

in cui N è la componente normale al piano inclinato di scorrimento ed f, coefficiente d’attrito, è dato dalla tangente dell’angolo d’attrito tra i due materiali a contatto (nel nostro caso j).

Componendo le reazioni T e –N, si ottiene la reazione complessiva R, rappresentata dal segmento 1-2”, ruotata dell’angolo j rispetto al vettore N. Questo perché, essendo T = Ntgj, T e N risultano cateti di un triangolo rettangolo in cui l’ipotenusa è rappresentata da R.

Dopo il cedimento del muro, quindi, il peso P deve essere scomposto in una componente perpendicolare al paramento e in una componente avente la direzione della risultante R. Il segmento 0-2’ rappresenta la spinta sulla parete, dopo il congruo cedimento, definita spinta attiva, e vale:

sostituendo l’espressione del peso P, otteniamo:

Spinta del generico prisma di terra ABX

Assumendo un altro piano di scorrimento BX’, inclinato anch’esso di un angolo a’>j e diverso da a, otteniamo la spinta attiva del prisma ABX’. Tra tutti i prisma di terra definiti da un piano di scorrimento con angolo j<a<90, occorre determinare quello che fornisce la massima spinta contro il muro, prisma che viene chiamato di massima spinta. Questo è il motivo per cui la teoria di Coulomb viene chiamata teoria del prisma di massima spinta.

Per determinare il valore della spinta massima, occorre determinare il massimo della funzione S nella variabile a, rappresentata dalla S_a, eseguendo la derivata prima e ponendola pari a zero.

il termine

rappresenta una costante, che chiamiamo K, quindi abbiamo

essendo tg(90-a) = cotga, sostituendo:

derivando e ponendo uguale a zero, si ha:

poiché K è un termine maggiore di zero, l’espressione tra parentesi quadra deve essere uguale a zero

eseguendo il minimo comune multiplo, che risulta

esprimendo la funzione tg e cotg, otteniamo

semplificando, l’espressione diventa

ricordando la formula di duplicazione della funzione seno, in cui

l’espressione diventa:

e, semplificando, abbiamo

Ricordando i teoremi sulla risoluzione delle equazioni goniometriche e, specificamente quello sull’equazione senx = m, che dice:

"due archi aventi lo stesso seno hanno la loro somma congruente ad un numero dispari di semicirconferenze"

applicando il teorema, ora esposto, alla nostra espressione, risulta:

con n numero intero. Limitando la ricerca alla prima semicirconferenza, abbiamo

dividendo per 2, abbiamo

infine, otteniamo

Angolo che individua il prisma di massima spinta

Lo stesso risultato si ottiene utilizzando un foglio di lavoro di ExcelÓ. Scriviamo l’espressione della spinta S_a di un generico prisma di terra

dopo aver stabilito l’angolo d’attrito interno j (per es. j=30°), determiniamo il valore dell’angolo a per cui l’espressione assume il valore massimo. Vediamo come impostare le formule nelle celle del foglio di lavoro, evidenziando che nell’utilizzo della funzione tangente occorre inserire gli angoli in radianti:

	A	B	C
1	j gradi	j radianti
2	30	=A2*pi.greco()/180
3	a gradi	a radianti	spinta
4	30	=A4*pi.greco()/180	=tan(pi.greco()/2-B4)*tan(B4-$B$2)

Nella tabella seguente si ricava, appunto, che il valore massimo del parametro S si ricava in corrispondenza dell’angolo a = 60°, corrispondente proprio a (90+j)/2, avendo stabilito j = 30° 

a^0	a^r	S	a^0	a^r	S	a^0	a^r	S
30	0,523599	0	50	0,872665	0,305407	70	1,22173	0,305407
31	0,541052	0,02905	51	0,890118	0,310847	71	1,239184	0,299319
32	0,558505	0,055885	52	0,907571	0,31566	72	1,256637	0,292559
33	0,575959	0,080701	53	0,925025	0,319865	73	1,27409	0,285098
34	0,593412	0,103671	54	0,942478	0,323478	74	1,291544	0,276907
35	0,610865	0,124947	55	0,959931	0,326512	75	1,308997	0,267949
36	0,628319	0,144664	56	0,977384	0,32898	76	1,32645	0,258187
37	0,645772	0,162941	57	0,994838	0,33089	77	1,343904	0,247576
38	0,663225	0,179884	58	1,012291	0,332249	78	1,361357	0,236068
39	0,680678	0,195588	59	1,029744	0,333062	79	1,37881	0,223609
40	0,698132	0,210138	60	1,047198	0,333333	80	1,396263	0,210138
41	0,715585	0,223609	61	1,064651	0,333062	81	1,413717	0,195588
42	0,733038	0,236068	62	1,082104	0,332249	82	1,43117	0,179884
43	0,750492	0,247576	63	1,099557	0,33089	83	1,448623	0,162941
44	0,767945	0,258187	64	1,117011	0,32898	84	1,466077	0,144664
45	0,785398	0,267949	65	1,134464	0,326512	85	1,48353	0,124947
46	0,802851	0,276907	66	1,151917	0,323478	86	1,500983	0,103671
47	0,820305	0,285098	67	1,169371	0,319865	87	1,518436	0,080701
48	0,837758	0,292559	68	1,186824	0,31566	88	1,53589	0,055885
49	0,855211	0,299319	69	1,204277	0,310847	89	1,553343	0,02905

Realizzando il grafico dei valori in tabella, osserviamo che il massimo della funzione risulta proprio in corrispondenza dell’angolo a = 60°; in corrispondenza dell’angolo a = j e dell’angolo a = 90° il coefficiente di spinta risulta nullo.

L’angolo a, ora determinato, individua il piano di scorrimento che racchiude il prisma di massima spinta; questo piano è individuato dal piano bisettore dell’angolo 90-j. Infatti, sostituendo ad a il valore trovato, abbiamo

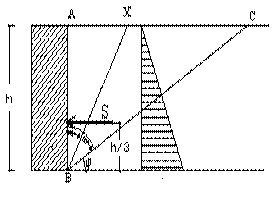
ABX prisma di massima spinta diagramma delle pressioni spinta S applicata ad h/3 dalla base

Sostituendo il valore dell’angolo a nell’espressione della spinta, abbiamo

Ottenendo, infine

formula fondamentale della Spinta di Coulomb in un terrapieno senza sovraccarico

Il diagramma delle pressioni, di cui la spinta S è la risultante, varia con andamento lineare essendo funzione dell’altezza h del terrapieno. Infatti, per definizione, la pressione è data dalla forza agente sull’unità di superficie, nel nostro caso abbiamo

in cui sostituendo

semplificando h, otteniamo

Cioè, la pressione p dipende direttamente da h.

Quando il terrapieno è scarico la pressione in sommità è nulla mentre alla base, ricordando che la spinta S_a rappresenta la risultante del diagramma delle pressioni, abbiamo:

Pressione massima alla base del muro

Spinta di Coulomb in un terrapieno con sovraccarico uniforme

Analizziamo, ora, il caso di un terrapieno orizzontale soggetto ad un carico uniforme.

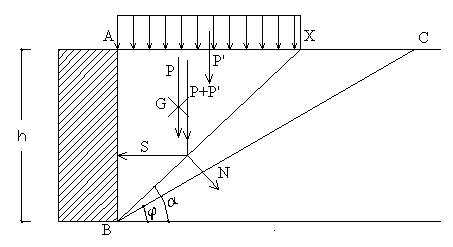
Terrapieno orizzontale con sovraccarico uniforme

Immaginiamo di sostituire il sovraccarico Q (KN/m²) con uno strato di terra di altezza h’ avente lo stesso peso specifico g_t del terrapieno, cioè:

	che ci fornisce
	altezza di uno strato di terra fittizio equivalente al sovraccarico Q

La teoria di Coulomb, precedentemente esposta, rimane ancora valida in tutti i suoi punti fondamentali; cambia solamente il peso del prisma di terra di massima spinta che deve tener conto anche del peso dovuto al sovraccarico. La sommatoria dei pesi vale P+P’, con

sostituendo i valori di AB e AX abbiamo:

moltiplicando e dividendo per 2h il secondo addendo dell’espressione, si ha

mettendo in evidenza, otteniamo

Ricordando l’espressione del peso di un generico prisma di terra in un terrapieno senza sovraccarico:

notiamo che esso differisce dal peso del prisma di un terrapieno sovraccaricato solamente del coefficiente amplificativo

Il prisma di massima spinta è sempre individuato dall’angolo a, come determinato nel caso di terrapieno senza sovraccarico, per cui la spinta S_a risulta

formula della Spinta di Coulomb in un terrapieno con sovraccarico uniforme

Il diagramma delle pressioni sul muro risulta trapezoidale con valori p_min in sommità e p_max alla base, mentre la spinta S_a, dovendo essere applicata nel baricentro del diagramma trapezoidale delle pressioni, risulta un po’ più sopra di h/3.

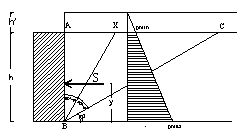
ABX prisma di massima spinta diagramma delle pressioni spinta S applicata ad y dalla base

Vogliamo, appunto, determinare i valori della pressione alla base e in sommità del muro, nonché la distanza y della spinta S_a dalla base. Essendo due le incognite (p_min e p_max), occorre risolvere un sistema in cui

- nella prima equazione si pone la Spinta uguale all’area del diagramma delle pressioni;

- nella seconda equazione si scrive la proporzione tra triangoli simili rappresentativi delle pressioni su un muro alto h’ e alto h+h’

sostituendo nella seconda equazione la somma p_min+p_max che appare nella prima equazione

si sostituisce il valore di p_min nella prima equazione e si ricava p_max

eseguendo il minimo comune multiplo all’interno della parentesi tonda nella prima equazione

Ottenendo, così, i valori della pressione in sommità e alla base del muro.

Ricaviamo ora la posizione della spinta S, come distanza del baricentro del diagramma trapezoidale delle pressioni dalla base maggiore. Ricordiamo la formula del baricentro del trapezio:

- h = altezza del trapezio - B = base maggiore del trapezio - b = base minore del trapezio

sostituendo B con il valore di p_max e b con il valore di p_min

mettendo in evidenza

al numeratore e al denominatore

semplificando, infine, si ottiene

distanza della spinta Sa dalla base del muro