TEOREMA DI VARIGNON

Prima di enunciare e dimostrare il teorema di Varignon, vogliamo ricordare il concetto di momento statico:

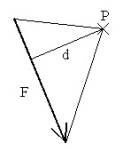
assegnata una forza F e un punto P, non appartenente alla retta d’azione della forza, il prodotto dell’intensità della forza F per la distanza d della sua retta d’azione da un punto P (centro del momento) rappresenta l’intensità del momento statico, mentre il verso di rotazione (orario o antiorario) dipende dalla posizione del punto rispetto alla retta di direzione della forza.

Cioè, l’intensità del momento è data da: M_S=Fxd.

Facciamo, ora, la seguente considerazione: se uniamo le estremità del vettore F con il punto P otteniamo un triangolo in cui la base è rappresentata dal vettore F e l’altezza dalla distanza d.

triangolo rappresentativo del Momento Statico

Ricordando che l’area di un triangolo è data dal prodotto

sostituendo b con il vettore F e h con la distanza d, otteniamo

Avendo definito M_S=Fxd, possiamo concludere che

Vale a dire, l’intensità del momento statico è rappresentata geometricamente dalla doppia area del triangolo che ha per base l’intensità della forza e per altezza la distanza della retta d’azione della forza dal punto P.

Diamo ora l’enunciato del teorema di Varignon (teorema fondamentale della statica):

“La somma algebrica dei momenti delle forze componenti un sistema rispetto ad un punto è uguale, in valore e segno, al momento della forza risultante del sistema rispetto allo stesso punto”.

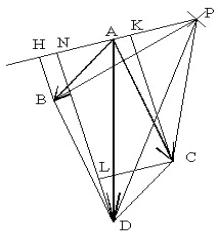
Per dimostrare quanto enunciato, prendiamo in considerazione, per semplicità, due forze aventi lo stesso punto di applicazione e come centro dei momenti il punto P. Mediante la regola del parallelogramma, determiniamo prima la risultante R del sistema di forze e, poi, uniamo le estremità delle forze e della risultante con il punto P. Otteniamo la seguente costruzione

in cui: AB = intensità della forza F1 AC = intensità della forza F2 AD = intensità della risultante R del sistema di due forze P = punto rispetto al quale calcoliamo i momenti ABP = vertici del triangolo la cui area rappresenta M1 ACP = vertici del triangolo la cui area rappresenta M2 ADP = vertici del triangolo la cui area rappresenta MR AP = base comune ai tre triangoli BH = altezza del primo triangolo CK = altezza del secondo triangolo DN = altezza del triangolo della risultante

L’enunciato del teorema di Varignon è valido se dimostriamo la seguente relazione:

Per quanto detto nella premessa, sostituiamo l’intensità dei momenti con il valore della doppia area dei triangoli formati dalle forze e dalla risultante con il centro dei momenti

esprimiamo, ora, le aree dei triangoli

semplificando AP, comune ai tre termini, e il 2, otteniamo

cioè, il teorema di Varignon è valido se dimostriamo che la somma delle due altezze BH e CK risulta uguale all’altezza DN del triangolo della risultante. Per fare questo, tracciamo dal punto C una parallela alla base comune AP sino ad incontrare l’altezza DN, ottenendo il punto L.

L’altezza DN può essere quindi scomposta nei segmenti DL e LN, cioè

e, quindi, occorre dimostrare la relazione

* espressione da verificare

Osservando i triangoli CDL e ABH, notiamo che sono simili in quanto i lati sono tra loro paralleli, ed essendo i lati AB e DC uguali in quanto lati opposti del parallelogramma delle forze, possiamo dire che sono uguali anche i lati BH e DL. Cioè

Ancora, osservando la figura, possiamo vedere l’uguaglianza tra CK e LN in quanto lati opposti del rettangolo KCLN, ottenuto per costruzione. Cioè

Risulta quindi dimostrata la relazione *. Ma essendo valida questa relazione, risulta anche valido l’enunciato del teorema di Varignon, che risulta, quindi, dimostrato.