Capitulu segundu
Una oghiadedda a su logu de Mathematica
Su programma Mathematica est una aliaga potente e adeguada meda a faer contos, programmare, analitzare datos, rapresentare in grafica e amustrare informatziones. Mancari cantu nadu siat beru, in custu triballu puntamus masprestu a pesare s'interessu de sos lettores a sas prestatziones bellas de su limbazu artificiale de su cales faimus s'analis, tenende presente e craru cantu custu argumentu siat relatzionadu cun sos ateros inantis pesados. Est disizu nostru iscrier programmas po tenner azudu in contos mannos chi potzan esser posca rapresentados in manera grafica chi nos cunsentat de torrare a bella bista su problema susu su cale semus peleande. Faimus in custu capitulu una introdutzione elementare de sas operatziones disponibiles, e pagos tzinnos han a esser bastantes a ponner in bella mustra sa irrichesa de custu limbazu.
2.1
Computos simbolicos e numericos. Mathematica est diferente de una calculatrice e de tantos programmas de elaboradores de datos po s'abilidade chi tenet de calculare risultados esatos e computare in d'unu gradu de pretzisione arbitraria.
2/3+4/5
22
--
15
1111111^2
1234567654321
765*432-123456^7+8901234/5678*(90123-4567)
72996473991016881840523394687485453596
-(--------------------------------------)
167
3^300
1368914790585883759913260273820883159664636956253374364\
714801900783689971774990765938002061556889413882504844\
40597994042813512732765695774566001
Ca custu numeru est fattu de tantas cifras chi ocupan tantas rigas su simbolu linea travessa (/) est impreadu comente a unu marcadore po indicare ca s'arresposta si cumpletat in sas lineas sighentes. Si podet amustrare custu numeru in notatzione issientifica esponentziale cun sa funtzione N[], est una forma brevis de pedire a su calculadore unu valore numericu, e fintzas tantas ateras cosas:
N[3^300]143
1.36891 10
Cando unu impreat sa funtzione pre-parada N[] disizat a tenner unu valore aprossimadu de una espressione chi cumportat numeros. Sa raighina cuadrada de chimbanta nos benit torrada incalculada, in termines de simbolos, fintzas a cando no dda pedimus cun N[].
Mathematica connoschet medas costantes de importu. Si poden ottenner valores aprossimados in cantas cifras si disizan. Contivitzade sos esempios.
Sqrt[50]
5 Sqrt[2]
N[Sqrt[50],20]
7.071067811865475244
{N[E],N[Pi],N[Log[E]],N[Log[2,1024]],N[Cos[Pi/3]],
N[ArcTan[1]]}
{2.71828, 3.14159, 1., 10., 0.5, 0.785398}
Expand[Sin[x]^2+Cos[x]^2,Trig->True]
1
Expand[] benit impreada po fortzare a una espansione simbolica de una espressione e sa optzione Trig->True cumbidat a su programma a impreare sas regulas pre-paradas po semplificare termines chi cuntenen funtziones trigonometricas. Comente in custu esempiu:
Expand[2 Sin[x] Cos[x],Trig->True]
Sin[2 x]
Cando unu cheret irboligare ecuatziones, naramus a agatareas raighinas de una ecuatzione cando issa ddas tenet, hamus a dispositzione medas possibilidades. Po ecuatziones chi poden esser isortas cun tecnicas alzebricas faziles enit impreada sa funtzione Solve. Sa ecuatzione de sugundu gradu ax^2+bx+c==0 a irboligare in x si triballat in custa manera:
Solve[a x^2+b x+c==0,x]
2
-b - Sqrt[b - 4 a c]
{{x -> ---------------------},
2 a
2
-b + Sqrt[b - 4 a c]
{x -> ---------------------}}
2 a
A s'ocasione capitat chi medas ecuatziones s'arrefuden de esser isortas cun tecnicas altzebricas, comente custa:
Solve[Cos[x]==x,x]
Solve::tdep:
The equations appear to involve transcendental
functions of the variables in an essentially
non-algebraic way.
Solve[Cos[x] == x, x]
S'imprean mancari metodicas numericas. FindRoot, agatta sas raighinas, est una funtzione pre-parada chi tenet contu de sa metodica de Newton. Custa funtzione arrechedet unu semene etadu acanta a inue si penzat sian sas raighinas:
FindRoot[Cos[x]==x,{x,0.1}]
{x -> 0.739085}
Sas funtziones pre-paradas faen fronte a totu sas netzessidades de su calculu. S'ordine de ischolas chi cunsideramus no istudian argumentos comente su calculu diferenziale e integrale e sas ecuatziones diferentziales, non de mancus presentamus calincunos esempios chena intrare meda in cosas detalliadas:
Integrate[a x^2+b x+c,x]
2 3
b x a x
c x + ---- + ----
2 3
D[Log[x],{x,1}]
1
-
x
Log'[x]
1
-
x
Integrate[Sin[x],{x,0,Pi}]
2
Integrate[E^Cos[x],{x,0,Pi}]
On::none: Message SeriesData::csa not found.
General::intinit:
Loading integration packages -- please wait.
Cos[x]
Integrate[E , {x, 0, Pi}]
N[Integrate[E^Cos[x],{x,0,Pi}]]
On::none: Message SeriesData::csa not found.
3.97746
2.2
Su limbazu cuntenet unu catalogu istraordinariu de funtziones po atire a cumprimentu contos issientificos. Paris a sas funtziones pre-paradas tantas ateras agatan su collocu issoro in sos packages. Cando benin abertos custos archivios sas possibilidades de computare aumentan meda. E in atzunta a totu custu su cliente de Mathematica podet isse e totu iscrier sas funtziones cantu e prus dd'agradan.
In teoria de numeros tenet impreu mannu s'aritmetica modulare. Sa funtzione Mod torrat su rimandu de una divisione intra duos numeros intreos. Si cunsideramus chenteunu divisu po chimbe, tando 101 est su dividendu, 5 su divisore, 20 su cuotziente e 1 su rimandu:
Mod[101,5]
1
Podimus tenner interessu a sos divisores de unu numeru
Divisors[28]
{1, 2, 4, 7, 14, 28}
Sa funtzione de Eulero torrat su numeru de totus sos intreos chi fun relativamente primos cun d'un'ateru numeru:
EulerPhi[22]
10
Sos pitzoccheddos de ischola istudian meda su binomiu de Newton iscobertu in su 1676:
Expand[(a+b)^2]
2 2
a + 2 a b + b
Expand[(a+b)^3]
3 2 2 3
a + 3 a b + 3 a b + b
Expand[(a+b)^4]
4 3 2 2 3 4
a + 4 a b + 6 a b + 4 a b + b
Expand[(a+b)^5]
5 4 3 2 2 3 4 5
a + 5 a b + 10 a b + 10 a b + 5 a b + b
Sos coeficientes de totu custas espansiones de sa potentzia de su binomiu si naran coeficientes binomiales. Su coeficiente de su kapaesimu termine in sa ennesima fila si computat cun Binomial[n,k]. Po esempiu su coeficiente de a^3b^2 est:
Binomial[5,2]
10
Sa linea cumpleta de sos coeficientes podet esser computada totu in d'una orta cun d'una funtzione cumposta chi giai giai est unu programma. Cumintzade a contivitzare su chi semus faende.
Table[Binomial[5,j],{j,0,5}]
{1, 5, 10, 10, 5, 1}
Table[espressione,{i,iminimu,imaximu}] arrechedet po generare una lista, posca de haer valutadu espressione,unu contadore i chi siat dispostu a leare su valore de totu sos numeros intreos, unu a unu si no diferentemente esplicadu, a mover de iminimu fintzas a imaximu.
Table[i^2,{i,1,5}]est impreadu po computare sos cuadrados de sos numeros intreos de unu a chimbe:
Table[i^2,{i,1,5}]
{1, 4, 9, 16, 25}
Sos coeficientes de su binomiu de Newton enin presentados in tabella, chi si narat triangulu de Tartaglia o triangulu de Pascal, in custa manera:
TableForm[
Table[
Binomial[n,k],{n,0,8},{k,0,n}]]
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
Chentinaias de propriedades aritmeticas de sos numeros fun relatzionadas cun su triangulu de Tartaglia. Po esempiu sa terta culunna cuntenet sos numeros triangulares. Unu kapaesimu numeru de Tartaglia est sa summa de sos primos kappa numeros:1+2+3+4...+k
Table[Binomial[n,2],{n,1,10}]
{0, 1, 3, 6, 10, 15, 21, 28, 36, 45}
Sum[i,{i,1,10}]
55
Table[Sum[i,{i,1,n}],{n,1,10}]
{1, 3, 6, 10, 15, 21, 28, 36, 45, 55}
E Gauss haiat iscobertu una formula po computare in presse sos primos chentu numeros intreos:
Binomial[n+1,2]
n (1 + n)
---------
2
Binomial[101,2]
5050
Sum[k,{k,1,100}]
5050
Crachi orta serbit a tenner a dispositzione una lista de numeros casuales. Po nde tenner unu intra de unu minimu e de unu massimu faimus Random[Real[,{0,5}]]. Si omitimus sos estremos si assumet chi su tretu siat intro de 0 e de 1. Si non si pedit unu tipu de numeros si assumet chi su tipu siat Real. Si poden pedire ateros tipos:
Random[Real,{7,10}]
7.96815
Random[Real]
0.634137
Random[]
0.754818
Random[Integer,{0,100}]
94
Sos numeros chi credimus sian casuales funi mancari pseudo random, casuales farzos, ma de custu fattu como no no si nde importat nudda.
2.3
Cando si traballat cun funtziones o cun imparis de datos netzessitat tantas bortas a ddos rapresentare in graficos. Custa faina est bella meda e de azudu mannu cando si disizat a incuadrare bene unu problema e sos irbolighinzos suos. Sa grafica podet esser bidimensionale e tridimensionale.
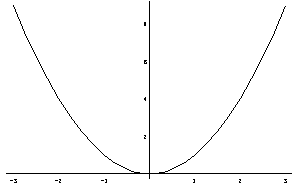
Sas funtziones de una variabile, est a narrer y=f(x), fun resas graficamente cun sa sa funtzione Plot[espressione,{variabile, lacana in giosso, lacana in susu}].
Plot[x^2,{x,-3,3}];

Est curiosu a faer graficos de totus sas funtziones connotas iscoberinde a manu a manu chi serbin totus sas optziones de su limbazu de programmatzione, chi ponet a dispositzione fintzas colores e russesa de sas lineas, graficos singulos e unu supra a s'ateru. Hamus haer ocasiones de riprender custos argumentos.
Plot[Sin[1/x],{x,-1,1},
PlotRange->{1.3,-1.3},
Ticks->None,
Axes->True];
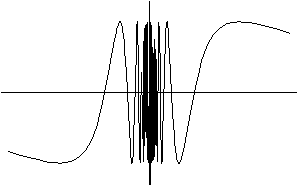
Medas bortas si podet tenner bisonzu de una funtzione in forma parametrica, sa prus connota est cussa de su cricu:
cricu=ParametricPlot[{Cos[t],Sin[t]},{t,0,2Pi}];
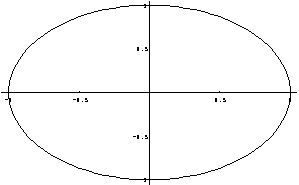
Non paret propriu su chi pensamus siat unu cricu, paret masprestu una ellisse. Ma a fortzare su programma po faer in modu chi unu cricu nos partzat unu cricu no est difitzile. Si depet cumprender chi totu sa grafica de su calculadore est preparada a tenner contu de su video chi no est cuadradu. Disativande AspectRatio, leada po default, totu sas cosas torrana a su zassu issoro:
Show[cricu,AspectRatio->Automatic];
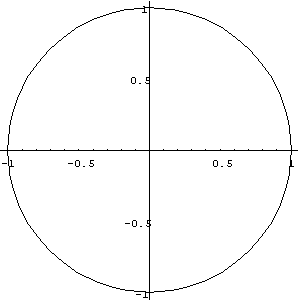
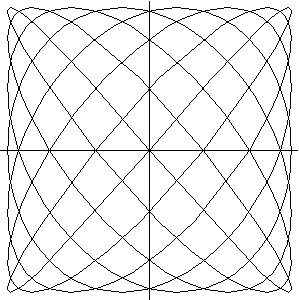
Custa atera curva si narat de Lissajous:
ParametricPlot[{Cos[7 t],Sin[8 t]},{t,0,2 Pi},
AspectRatio->Automatic,Ticks->None];
Si definimus una funtzione de duas variabiles dda podimus rapresentare graficamente
z[x_,y_]::=Cos[x]/Sin[3 y];
Plot3D[z[x,y],{x,-4Pi,4Pi},{y,-4Pi,4Pi},
PlotPoints->30];
2.4
Sa programmatzione. Sos utentes de onni limbazu de programmatzione iscoberin in presse chi sas funtziones pre-paradas non funi bastantes a soddisfaer totus sos disizos issoro de pesare contos. E tando issos puntan a iscrier programmas cumbinande funtziones pre-paradas cun ateras chi si preparan issos e totu. Sos programmas chi aparitzamus in custa setzione amustran sos costructos presentes in Mathematica: no nos ispetamus chi totu entzat cumpresu a sa prima mirada. Isperamus mancari chi siat apretziada sa bona volontade e chi siades abiles e interessados a torrare a lezer cantu como paret difitzile.
Sa serie armonica e sa summa de sos retziprocos de sos primos n numeros naturales. Custa serie est divertzente e si indicat in custa manera. H[n]=1+1/2+1/3+1/4+...+1/n.
Definimus nois una funtzione:
H[n_]:=Sum[1/k,{k,1,n}]
H est su numen de sa funtzione, su _ si narat blank e denotat sos argumentos de sa funtzione. Computamus calincunu de sos termines de sarie armonica:
H[4]
25
--
12
{H[20],N[H[20]]}
55835135
{--------, 3.59774}
15519504
Sa serie armonica divertzet, po n che tendet a s'infinidu sos termines suos faen ateretantu, ma in manera lesina. Su fattu est chi po calculare termines chi funi ancora piticos, comente H[100] si depet faer su minimu comunu multiplu de chentu numeros e summare chentu fratziones. Cun sos numeros aprossimados est prus fatzile a calculare:
NH[n_]:=NSum[1/k,{k,1,n}]
{NH[10^3],NH[10^6],NH[10^9],NH[10^12]}
{7.48547, 14.3927, 21.3005, 28.2082}
Sa diferntzia intra unu termine ennesimu de sa serie e su logaritmu naturale de enne est unu numeru de importu, connotu comente costante gamma de Eulero:
NH[10^12]-N[Log[10^12]]
0.577216
N[EulerGamma]
0.577216
Meda zente connoschet Pigrecu o sa costante E de Neperu, ma pagos ischin de pretzisu it'est sa costante de Eulero:Limit[NH[n]-N[Log[n]],n->Infinity]=EulerGamma. Pedimus custas costantes imparis:
{N[Pi,10],N[E,10],N[EulerGamma,10]}
{3.141592654, 2.718281828, 0.5772156649}
Si aberimus s'archiviu, (Package), SimbolicSum hamus sa possibilidade de ateros computos, fintzas in forma simbolica. A aberrer unu archiviu si faet gosi: si digitat de tastiera duas bortas su sinnu de minore:<< su numen de sa Directory Alt96 e su numen de s'archiviu serrande cun Alt96.Podimus otenner formulas bellas de matematicas non semper discanzosas a calculare in ateras maneras. Sas chi amustramus calculan sa summa de sos primos n termines de sa sutzessione de sos intreos, de sos cuadrados, de sos cubos, de sas cuartas potentzias e gasi a sighire.
<<Algebra`SymbolicSum`
Sum[i,{i,1,n}]
n (1 + n)
---------
2
Sum[i^2,{i,1,n}]
n (1 + n) (1 + 2 n)
-------------------
6
Sum[i^3,{i,1,n}]
2 2
n (1 + n)
-----------
4
Sum[i^4,{i,1,n}]
2
(-1 - n) n (1 + 2 n) (1 - 3 n - 3 n )
-------------------------------------
30
Sos archivios funi agiuntivos de Mathemathica. Su manuale de Istevene Wolfran nde faet unu elencu. Custu dat informatziones de chimicas:
<<Miscellaneous`ChemicalElements`
Wolfram
Tungsten
Abbreviation[Wolfram]
W
AtomicWeight[W]
183.85
HeatOfVaporization[W]
824.2 Joule Kilo
----------------
Mole
Gold
Gold
Abbreviation[Gold]
Au
2.5
Pesamus unu esempiu de unu programma a riguardu de sos numeros perfetos. Unu numeru intreu e positivu est perfetu cando est uguale a sa summa de sos divisores suos manch'issu e totu.
Divisors[6]
{1, 2, 3, 6}
Apply[Plus,{1,2,3}]
6
E tando ses est perfetu. Iscridimus una funtzione chi torret solu sos divisores proprios:
divisoresproprios[n_]:=Drop[Divisors[n],-1]
divisoresproprios[6]
{1, 2, 3}
Apply[Plus,divisoresproprios[6]]
6
Pentzamus unu preigadu chi nos torret beru o fartzu si s'argumentu suu est unu numeru perfetu o nono:
perfetuQ[n_Integer]:=Apply[
Plus,divisoresproprios[n]]==n
perfetuQ[6]
True
perfetuQ[16]
False
Nois como semus in gradu de analitzare unu tretu de numeros po ischire si a parte ses s'agatan ateros numeros perfetos. perfetuQ est unu criteriu e benit aplicadu po che ogare de una lista de numeros solu sos numeros chi passan su criteriu, e torrat True cando enit aplicada sa funtzione Select. Po esempiu, prima seletzionamus sos numeros paris de una lista de unu a chentu, o in sa matessi sos numeros disparis. Abaidamus posca si agatamus numeros perfetos.
Select[Range[100],EvenQ]
{2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28,
30, 32, 34, 36, 38, 40, 42, 44, 46, 48, 50, 52, 54,
56, 58, 60, 62, 64, 66, 68, 70, 72, 74, 76, 78, 80,
82, 84, 86, 88, 90, 92, 94, 96, 98, 100}
Select[Range[100],OddQ]
{1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29,
31, 33, 35, 37, 39, 41, 43, 45, 47, 49, 51, 53, 55,
57, 59, 61, 63, 65, 67, 69, 71, 73, 75, 77, 79, 81,
83, 85, 87, 89, 91, 93, 95, 97, 99}
Select[Range[100],perfetuQ]
{6, 28}
Che nd'hamus ogadu un'aterunu, 28. E tando podimus iscrier una funtzione po seletzionare in d'unu tretu de numeros, mannu cantu nos praghet, sos numeros perfetos:
perfetos[n_]:=Select[Range[n],perfetuQ]
perfetos[1000]
{6, 28, 496}
Su programma est debile in cantu a lestresa de computu. Sos numeros perfetos ponen chistiones de importu, cales si sian infinidos, si sian solu paris o si nd'agaten disparis. Si nde tenides gana ponidebos in crica.