home


Capitulu septimu
Sa pregunta de tiu Goldbach

Sos numeros paris si poden rapresentare totus comente una summa de duos numeros primos?

7.1

Unu limbazu, siat issu naturale o artefattu, no est tale si no nos permitit de esprimer cunzetos de sa mente, arresonamentos de sa conca e chistiones, chistiones mannas susu de sas cales si funden posca sas teorias chi esplican su mundu inue bivimus, e sas matessis teorias, cando pagu cundivididas si pothan abandonare.
Una problematica de importu in matematica est istada pesada a Lenardu Eulero da e unu ateru matematicu chi si narąda Cristianu Goldbach in su 1742. Sa chistione, si no ateru est curiosa, ca de tando mancari in medas ddu epan tentadu, nemos est renessidu a dda isorbere. E nemancu Eulero, po cantu matematicu de importu esseret est renessidu a risponder in manera zenerale a su problema. Unu numeru paris, cales funi sos multiplos de duos, narąt Goldbach, si podet semper rapresentare comente summa de duos numeros primos, cales funi po esempiu tres, chimbe, sette e undighi, e tantos ateros ancora, essende chi funi infinidos. Su fattu paret evidente e craru che su sole: deghe po esempiu si podet otenner summande in tra issos tres e sette, doighi summande chimbe e sette, e batordighi undighi e tres. Po cantu epan chircadu de cunfutare sa ipotesi de Goldbach mai nissunu at ottentu unu esempiu in contrariu: hamus a narrer unu numeru paris chi non esseret summa de duos numeros primos.
Una ricurrentzia gasi evidente depet tenner una dimustrazione in matematica. A narrer totu sa beridade no est semper gasi, o a su mancus sa chistione no est gasi semplice e in paris. B'hat istadu in su seculu coladu unu matematicu, Kurt Godel, chi hat amustradu a totu sa zente chi s'agatan semper propositziones indezidibiles in totus sos limbazos formales chi si fundan susu sos assiomas de sos Principia Mathematica de Russel e susu sos assiomas de Zermelo-Fraenkel e sistemas similes, hamus a narrer chi siant simbizantes meda a s'aritmetica nostra de d'onnia die.
Non si discutit chi onni matematicu diletante, comente podimus esser noisateros, no epat perdidu mai ocasione de si misurare cun sa supositzione de Tiu Goldbach, e semper epat annunziadu a su mundu de aer agatadu una dimustratzione, semper farza, de su teorema. E nois podimis essere de mancu? Pretzisu chi nono. Nois in prus semus cunbintos chi a si misurare cun custos problemas serbit, po imparare a connoscher sas chistiones e po cumintzare a ischire cantu costat su trigu in Semestene: hamus a narrer cantu suore e impinnu ddu e cherzat a istudiare e a proponner a sos ateros una opinione. Mancari poi zusta non siet.

7.2

Goldbach, sa cales chi, segundu medas criticos e istudiosos, paret rientret in tra cussas propositziones de sa matematica chi Godel ritenet indetzidibiles, cantu a amustrare chi si podet analitzare su contu impreande aliagas matematicas connotas e fetianas. Isvilupande unu arresonamentu arSa idea chi nos apiliscat no est tantu de dimustrare sa cunzetura de Cristianuitmeticu immediatu s'incapat luego in d'una funtzione de sa cale nezessitat a nde connoscher una primitiva, nde depimus in pagas paraulas calculare s'integrale indefinidu: est una de sas tantas funtziones chi no amitini una primitiva esprimibile cun funtziones elementares. E tando in cue nos frimamus. Masprestu chircamus de afrontare s'argumentu segundu unu puntu de bista istatisticu, cosa chi nos permitit de otenner in modu graficu su fenomenu chi andamus istudiande, est a narrer a bier e comente suzedit chi totus sos numeros paris poden esser otentos de una summa semper de duos numeros primos. A calculare numeros primos mannos no est cosa fazile, resurtat difitzile meda a dimustrare si unu numeru mannu est primu o nono. Ma po numeros piticcos sa cosa no nos ponet pensamentu. E poi cun d'una tecnica de su calculu cumbinatoriu faghimus totu sas accoppiadas de sos numeros primos chi hamus ottentu, e nde faghimus sa summa de sas coordinadas, e abbaidamus si po casu carchi numeru paris fartat de essere in elencu. Si fartat Goldbach tenet tortu, si nono no est chi tenzat arresone, ma a ddi narrer chi tenet tortu ddu e nde colat ancora.

estprimu[n_Integer]:=
Apply[Plus,Divisors[n]]==n+1;
numerosprimos[n_]:=
Select[
Range[n],estprimu];
elencudeprimos=numerosprimos[300];
Table[elencudeprimos[[t]],{t,1,10}]

{2, 3, 5, 7, 11, 13, 17, 19, 23, 29}

arreddoppia[l_]:=
Partition[
Sort[
Flatten[
Append[l,l]]],2];
segunduelpr=arreddoppia[elencudeprimos];
Table[segunduelpr[[t]],{t,1,10}]

{{2, 2}, {3, 3}, {5, 5}, {7, 7}, {11, 11}, {13, 13},
{17, 17}, {19, 19}, {23, 23}, {29, 29}}

Che canzellamus de custu elencu de accoppiadas de numeros primos sa chi est unu doppiu duos, o mancari de s'elencu de sos numeros primos che canzellamus su duos; duos summadu a sos ateros primos chi funi disparis no nos faer ottenner numeros paris.

terzuelencudeprimos=Delete[elencudeprimos,1];
Table[terzuelencudeprimos[[t]],{t,1,10}]

{3, 5, 7, 11, 13, 17, 19, 23, 29, 31}

E tando:

cuartuelencudeprimos=arreddoppia[terzuelencudeprimos];
Table[cuartuelencudeprimos[[t]],{t,1,10}]

{{3, 3}, {5, 5}, {7, 7}, {11, 11}, {13, 13}, {17, 17},
{19, 19}, {23, 23}, {29, 29}, {31, 31}}

7.3

Como pesamus una funtzione chi cumbinet a duos a duos totu sos numeros primos, farta duos chi hamus eliminadu. Otenimus tantas coppias de numeros ,e amentamus chi sos elementos de una coppia si naran coordinadas. Custas coordinadas ddas hamus a summare s'una cun s'atera e nd hamus a incunzare numeros paris.
Sa funtzione chi faghet custu dda mutimus provvisoriamente sutaimparis, e hat a tenner po argumentu suu unu imparis, (de numeros primos a su chi nos riguardat), e po segundu argumentu unu numeru chi ispezifichet de cantos elementos est sa cumbinatzione cunsiderada. Custa funtzione triballat cun cale si siat imparis, e calculat sos suta imparis de cale si siat imparis finidu. Dda faghimus triballare a prima cun d'unu imparis de literas de s'alfabetu e posca senza avisare prus cun s'elencu de numeros primos de tres a binti: cuartuimparisdeprimos.


sutaimparis[j_List,0]:={{}}
sutaimparis[j_List,1]:=Partition[j,1]
sutaimparis[j_List,k_Integer?Positive]:={j}/;(k==Length[j])
sutaimparis[j_List,k_Integer?Positive]:={}/;(k>Length[j])
sutaimparis[j_List,k_Integer?Positive]:=
Join[Map[(Prepend[#,First[j]])&,
sutaimparis[Rest[j],k-1]],
sutaimparis[Rest[j],k]];
sutaimparis[{a,b,c,d},2]

{{a, b}, {a, c}, {a, d}, {b, c}, {b, d}, {c, d}}

sutaimparis[{3,5,7,11,13,17,19},2]

{{3, 5}, {3, 7}, {3, 11}, {3, 13}, {3, 17}, {3, 19},
{5, 7}, {5, 11}, {5, 13}, {5, 17}, {5, 19}, {7, 11},
{7, 13}, {7, 17}, {7, 19}, {11, 13}, {11, 17},
{11, 19}, {13, 17}, {13, 19}, {17, 19}}

Pesamus como unu sutaimparis prus mannu, e no ddu amustramus a video ca haiat a arrecherrer medas pazinas, de sos numeros primos de unu a chentu, farta duos, e chi si mutit terzuimparisdeprimos. Custu ateru ozetu ddu mutimus cuintu, a issu unimus in su sensu de sa teoria de sos imparis cuartuelencudeprimos, chi poi funi sas coppias, sas coordinadas de sas cales funi numeros primos ripetidos, e ddi ponimus numen sestu. Si cherimus ier unu elementu de sestu, ischimus comente fagher.

cuintu=sutaimparis[terzuelencudeprimos,2];
sestu=Partition[
Flatten[
Append[cuintu,cuartuelencudeprimos]],2];
Table[sestu[[t]],{t,100,110}]

{{5, 191}, {5, 193}, {5, 197}, {5, 199}, {5, 211},
{5, 223}, {5, 227}, {5, 229}, {5, 233}, {5, 239},
{5, 241}}


E como summamus sas coordinadas de custas accoppiadas de numeros primos. A s'imparis ddu mutimu summaprima.

summaprima=Apply[Plus,sestu,2];
Table[summaprima[[t]],{t,100,130}]

{196, 198, 202, 204, 216, 228, 232, 234, 238, 244, 246,
256, 262, 268, 274, 276, 282, 286, 288, 298, 18, 20,
24, 26, 30, 36, 38, 44, 48, 50, 54}

Comente si podet ier, de onnia coppia de numeros primos, si si nde additzionant sas coordinadas si ottenet unu numeru paris. Unu matessi numeru paris podet esser ottentu summande coordinadas diferentes, comente deghe chi si ottenit summande tre e sette, chimbe e chimbe, sette e tres.
Nos importat a ischire in cantas maneras diferentes unu numeru paris si ottenet summande coppias de numeros primos. Pesamus una funtzione chi si narat safrecuentzia. In su esempiu chi proponimus sa frecuentzia de unu est tres. Nois calculamus sas frecuentzias de sas recurrentzias de sos numeros paris in s'imparis summaprima.

safrecuentzia[lista_]:=
Map[({#,Count[lista,#]})&,Union[lista]]
safrecuentzia[{1,1,1,2,2,2,2,2,2,3,3}]

{{1, 3}, {2, 6}, {3, 2}}

frecuna=safrecuentzia[summaprima];
Table[frecuna[[t]],{t,10,20}]

{{24, 3}, {26, 3}, {28, 2}, {30, 3}, {32, 2}, {34, 4},
{36, 4}, {38, 2}, {40, 3}, {42, 4}, {44, 3}}

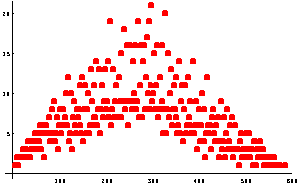
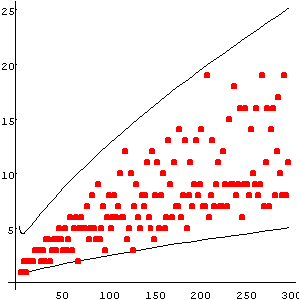
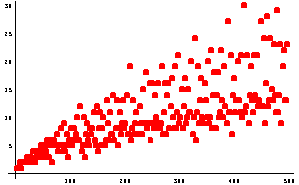
E faghimus unu graficu de totu custa frecuentzias:

graficusudeunu=ListPlot[frecuna,
PlotStyle->{RGBColor[1,0,0],
PointSize[0.015]}];

7.4

In su graficu su de unu podimus notare chi leande in cunsideru sos numeros primos prus piticcos de chentu e summandeddos a duos a duos ottenimus summas prus mannas de su numeru chentu, e a lacana cun duas bortas chentu. Nos importan sos numeros paris finas a chentu solu, e po fagher custu pesamus una funtzione, su sensu de sa cale est evidente: issa seletzionat in d'unu imparis sos numeros e chi sian minores de un'aterunu istabilidu.

minoresdeN[n_Integer]:=n<300;
sel[w_List]:=Select[w,minoresdeN];
arapresentare=sel[summaprima];

frecduas=safrecuentzia[arapresentare];
graficusudeduos=ListPlot[frecduas,
PlotStyle->{RGBColor[1,0,0],
PointSize[0.015]}];

In custu graficu, in s'ascissa enin rapresentados totus sos numeros paris de batoro finzas a chentu, e in s'ordinada sas frecuentzias segundu sas cales onnia numeru paris podet esser ottentu additzionande tra issos duos numeros primos: notamus chi a manu a manu chi sos numeros paris creschent, creschen puru sas frecuentzias e posca chi su graficu andat ocupande unu ispatziu semper prus in artu, semper prus lontanu de s'asse de sas ascissas. Custu cherrer narrer chi duas funtziones de una matessi famillia allacanan sa distribuztzione chi semus leande in cunsideru. Cale podet esser una funtzione de custu tipu si nd'esistit una?
Sa distributzione de sos numeros primos in tra tres e n sighit una leze asintotica de custu tipu: si A(n) est su numeru de sos primos intra tres e n tando (A(n)/n)/(1/Log[n]) tendet a 1 si n est mannu meda.
Custu cheret narrer chi A(n) est aprossimativamente uguale a n/Log[n].
A partire de custu fattu est possibile torrare una istima po onni numeru paris cantas funi sas coppias de numeros primos chi, summande sas coordinadas suas, mi torren propriu cussu numeru paris.
In ascissa ddu hat a esser tando su numeru paris e in ordinada sa frecuentzia de sa cales semus arresonande.
Custa funtzione dipendet de unu parametru chi andat calculadu segundu s'esperientzia chi si tenet de sa distributzione, ma paret chi tenzat una lacana inferiore e una superiore. Po contu nostru ponimus sa prima uguale a 1.117232735 e sa segunda a chimbe ortas custa.

Clear[k]
inf[n_]:=((n/Log[n]-2)*(n/Log[n]-1)*1/2+n/Log[n])*k/n
Expand[inf[n]]

k              k                           n k
-   +      ---------          -        --------
n               2                   2 Log[n]
        2 Log [n]


Custa espressione enit semplificada e fatta uguale a zero incuntzandecche (n/Log[n])^2-n/Log[n]+2==0, dividinde totu po k/2 e ordinande.Ponende a pustis y=n/Log[n] si pervenit a una ecuatzione de segundu gradu y^2-y+2==0. Isorbendedda non s'agatan raighinas reales. Cherrer narrer chi sa famillia de curvas chi allacanan sa distribuzione no atopan mai s'asse de sas ascissas. Nessunu numeru paris tenet tando una frecuentzia uguale a zero in sa rapresentazione comente summa de duos numeros primos. E tiu Goldbach teniat arresone, mancari a nois e totu custa dimustratzione parzat ancora mancante.

Solve[y^2-y+2==0]

           1 - I Sqrt[7]            1 + I Sqrt[7]

{{y -> -------------}, {y -> -------------}}
                   2                                2
inf[n]
            n                   n
(-2 + ------) (-1 + ------)
        Log[n]         Log[n]                n

k (--------------------------- +          ------          )
                2                             Log[n]
----------------------------------------
                        n

k=1.11317232931

1.11317232931

infgraf=Plot[inf[n],{n,4,300},
AspectRatio->1,Axes->True,
AxesOrigin->{0,0}];

sup[n_]:=((n/Log[n]-2)*(n/Log[n]-1)*1/2+n/Log[n])*h/n
h=5*1.11317232931
5.56586
supgraf=Plot[sup[n],{n,4,300},
AspectRatio->1,Axes->True,
AxesOrigin->{0,0}];

Show[supgraf,infgraf,graficusudeduos];

7.5

De totus sos arresonamentos c'hamus fattu nd iscridimus tando unu programa.


BeginPackage["myfrau`cometa`"];
cometa::usage="cometa[n] pintat su graficu de sas
frecuentzias cun sas cales podet esser esprimidu unu
numeru paris comente summa de duos numeros primos,";
Begin["`Private`"];

primoQ[n_Integer]:=Apply[Plus,Divisors[n]]==n+1;
numerosPrimos[n_]:=Select[Range[n],primoQ];

KS[l_List,0]:={{}}
KS[l_List,1]:=Partition[l,1]
KS[l_List,k_Integer?Positive]:={l}/;(k==Length[l])
KS[l_List,k_Integer?Positive]:={}/;(k>Length[l])
KS[l_List,k_Integer?Positive]:=
Join[Map[(Prepend[#,First[l]])&,
KS[Rest[l],k-1]],
KS[Rest[l],k]];

radd[n_Integer]:=
Partition[Sort[Flatten[Append[
numerosPrimos[n],numerosPrimos[n]]]],2];

comb[n_Integer]:=KS[Delete[numerosPrimos[n],1],2];

freq[l_List]:=
Map[({#,Count[l,#]})&,Union[l]];

cometa[j_Integer]:=
Module[{b=j},
minN[n_Integer]:=n<b;
a=Sort[
Apply[
Plus,
Partition[
Flatten[
Append[comb[b],radd[b]]],2],2]];
ListPlot[freq[Select[a,minN]],
PlotStyle->{PointSize[0.015],RGBColor[1,0,0]}];
Clear[a]];

End[];
EndPackage[]

grafudef=cometa[500]

7.6

Su chi cherimus pesare a notu no est tantu sa zustesa de sa dimustratzione chi amus presentadu. Podet esser una dimustratzione chi in carchi passazu fartat, e nois e totu nde semus pagu cumbintos. Sa cosa de importu est chi de unu problema de sas matematicas mannas, cun s'azudu de una aliaga comente su calculadore nd'epemus potziu analitzare sos aspetos prus prufundos e cuados. Ma su chi importat a unu maistru de ischola est mancari a essere arrennessiu a presentare una chistione e haer fattu a cumprender chi si nd agatan areras chi ispetan intelligentzias friscas a ddas irboligare.

home