sa lista est un ordine a su programma po rappresentare sa funtzione de terzu gradu
in su tretu de numeros reales chi incumintzat cun -1 e acabat a 1.O fintzas:
Integrate[Cos[x],{x,0,Pi/2}]
1
Sa funtzione Cos[x] est istada integrada intra sos estremos de integratzione zero
e metade de pigrecu.
Cando una espressione benit terminada cun d'unu puntu e virgula su valore suu enit si,
computadu, ma no amustradu a video, imprentadu, e custu fattu est unu azutoriu mannu cando
sos risultados inter-medios funi longos meda e de pagu importu a esser indagados a fundu.
Clear[F]
F[0]:=1
F[1]:=1
F[n_]:=F[n]=F[n-2]+F[n-1]
F[20]
10946
N[F[50]/F[49],10]
1.618033989
N[GoldenRatio,10]
1.618033989
Su programma chi hamus iscrittu calculat sos numeros de Fibonacci. Hamus a torrare
susu custu argumentu cando hamus a esser prus capazos de intender sas tematicas de
programmatzione. Sos numeros de Fibonacci forman una sutzessione de numeros meda famada, e
chi tenet tantas caracteristicas matematicas de esser impossibile, a chie apena apena
dezidit de istudiare custa disciplina, a dd'ignorare. Custa sutzessione de numeros si
format a partire de duos semenes, 1 e 1, chi funi tando sos primos duos termines de sa
sutzessione. Onni termine sighente si ottenet de sos duos a luego pretzedentes sommados a
pare. Tando su tertzu termine est tres, su cuartu est chimbe, e posca otto e treghi e
bintunu e gasi sighinde a computare. Ma non ddue hat bisonzu de calculare totu sos
termines finas a su e binti po ischire cantu si alet:
su valore suu est 10946. E gasi non depimus calculare cantu est su valore de su
chimbantesimu termine e de su barantanoesimu po nde faer su rapportu: issu alet
1.618033989 , chi est unu numeru de importu in matematica e si narat setzione de oro.
Una espressione podet esser inputada in Mathematica in varias lineas, ma solu si
Mathematica podet cumprender chi s'inputu in d'una linea no est finidu. Po esempiu si
podet inputare:
3*
4
12
Ma nono
3
*4
3
Syntax::sntxb: Expression cannot begin with "*4".
Su trubullu si evitat impreande sas parentis:
(3
*4)
12
In su fozu de triballu, (Notebook), si poden inputare medas lineas, Mathematica
ddas valutat solu cando s'ordine Shift+Enter enit issu puru inputadu. Si poden puru, riga
a riga, o cando agradat, o cando ddu est su bisonzu, intrare in mesu cumentos e notas
personales, si narat a documentare su triballu, bastat chi custa documentatzione siat
iscritta intro de parentis tundas e istedditos: (*custu est unu cummentu*):
D[Sin[x],(*su diferenziale de Sin[x]*)
{x,1}] (*cun respectu a x, una orta*)
Cos[x]
Expand[(a+b) (a-b) (*unu produttu notevole*)]
2 2
a - b
1.5
Sa die de sa festa de Santu Juanne, in
bidda, hamus fattu su fogu! Fudi mannu meda e totu sa zente si firmiat a l'abaidare. A
perras de manzanu, su fogu, haiat incominzadu a miminare fintzas a cantu est addurada solu
sa chisina. Deo e un amigu meu l'hamos brincadu e hamos fattu unu zuramentu: da e cussa
die semus diventados compare e comare. Cappai I.
A s'internu. E cale est sa forma de sa rapresentatzione interna de una
espressione.
Cando unu faet unu calculu aritmeticu semplice comente podet esser 1+2*3 non ponet tantu
advertentzia a comente Mathematica si apresentat a s'internu suu sos datos po podet
torrare unu resultadu. Ma est semper faina de importu a esser capatzos de ischire cale est
sa rapresentatzione interna de onni espressione; ischire custu fattu nos podet esser de
azudu po amanipulare unu numeru mannu de espressiones cun siguresa e lestresa. Mathematica
riunit inparis sos ogettos cun sos cales operat in tipos diferentes de datos.
Sos numeros intreos funi distintos de sos numeros reales. Sas listas funi distintas de sos
numeros. Una arresone de custu fattu est ca servit a identificare sos tipos de datos po
impreare algoritmos ispecializados po faer contos lestros a segunda de sas classes de
otzetos leadas in cunsideru.
Sa funtzione Head si impreat po identificare sos tipos de datos. Po numeros semplices issa
iscoviat si unu numeru est intreu, ratzionale,reale e a gasi a sighire:
{Head[7],Head[3/4],Head[.7],Head[1+I]}
{Integer, Rational, Real, Complex}
Difattis onni espressione matematica hat unu Head chi nos tenet informados de su
tipu suu:
Head[a+b]
Plus
Head[{1,2,3}]
List
Sa rapresentatzione interna de s'espressione nos benit dada impreande FullForm. Po
esempiu sa espressione a*b benit imagasinada in sa forma:
FullForm[a*b]
Times[a, b]
FullForm[{1,2,3}]
List[1, 2, 3]
Si depet notare chi s'operadore binariu a*b est aberu rapresentadu a s'internu in
forma funtzionale usande sa funtzione pre-parada Times. Issa moltiplicat sos argumentos
suos:
Times[2,3,4]
24
Cando si tratat de espressione cun imbolighinzos mannos sa rapresentatzione
interna no est fatzile de detzifrare:
FullForm[x^3+a x^2+b x+c==0]
Equal[Plus[c, Times[b, x], Times[a,
Power[x, 2]],
Power[x, 3]], 0]
In finis su chi est de importu est a s'arregordare chi onni espressione podet
esser usada e inputada in sintassi funtzionale. Sa forma istandard in sa cale si inputan
sas espressiones, inue s'operadore cumparit in tra sos operandos, est zustu una manera
prus discanzosa po iscrier aplicatziones. Esistin formas prefissas, infissas e postfissas.
1.6
Forma postfissa. Comente hamus bistu deinantis, onni funtzione in Mathematica
podet esser iscritta in sa forma Head[arg1,arg2,arg3...argn]. In manera occasionale si
podet agatare cumbeniente a impreare ateruna forma connota comente postfix form. A su
postu de iscrier s'espressione f[expr] iscridimus expr//f. Po esempiu:
x^5-1//Factor
2 3 4
(-1 + x) (1 + x + x + x + x )
Factor[x^5-1]
2 3 4
(-1 + x) (1 + x + x + x + x )
Ma podet capitare, triballande po computos o cun programmas, a faer atopos cun
irballios de tipos varios, calincunos maduros e ateros fines, medas discanzosos a
curretzer e ateros po sos cales non s'agatat versu. Po esempiu si podet intrare in d'unu
ciclu infinidu, e in custa evenientzia si no hais s'eternidade a dispositziones bostras
s'unica cosa de faer est a firmare su computu. Discutimus in custa setzione de cuddas
situatzione inue Mathematica finit unu contu e mancari sos contos non torran.
Unu errore frecuente est cussu de irballiare iscriende su numene de una funtzione. Faimus
bier calincunu de custos tipos de trobeddaduras;
Sine[Pi]
General::spell:
Possible spelling error: new symbol name "Sine"
is similar to existing symbols {Line, Sin, Sinh}.
Sine[Pi]
Plote[Sin[x],{x,0,Pi}];
General::spell1:
Possible spelling error: new symbol name "Plote"
is similar to existing symbol "Plot".
Cando inputas una funtzione e su numen s'assimbizat a un'ateru, su programma
inprentat una nova de errore. Inantis Mathematica hat torradu sas espressiones
invalutadas. Fintzas a cando issu no hat a ischire e ite cherrer narrer Sine, torrat
s'espressione chi ddu cuntenit sena dda computare. In custas evenientzias semplitzes est
bastante a curretzer sa causa de s'errore, est a narrer digitande in manera curretta su
numen de sa funtzione seberada.
Ateras bortas Mathematica faddit sos contos. Ma tenet semper risorsas mannas :
N[Integrate[1/x,{x,10^(-10),10^1}],10]
25.32843602
N[Integrate[1/x,{x,.1,1}]]
2.30259
1.7
Cando fui pitzinna happo semper amadu sos caddos, ma mama e babu no m'hana mai azuadu a
m'imparare a setzer. So istada faghinde fintzas chi bi so' resultada. M'happo chilcadu unu
caddu e happo imparadu. So' essida a sa festa de Nostra Sennora de Corte, happo preparadu
su caddu in domo, e prima de ch'essire mama m'hat dadu a bufare unu ticcu de abba, e
s'atera che l'hat bettada in conca a su caddu.
A mie non piaghen custas cosas e cando happo cumpresu chi fudi sa meighina de s'oggiu mi
so' arrennegada meda, e mi piaghet ancora a sezzer a caddu. Sechi A.F
Preigados. A prus de esser bonos a ischire su tipu de datos cun sos cales cherimus
triballare medas bortas nos presentat su problema de detzider si sos datos nostros passan
talunos criterios. Unu preigadu est una funtzione chi torrat unu valore, beru (True) o
fartzu (False) in dipendentzia de su fattu chi sos argumentos suos sian abiles a passare
unu test. Po faer unu esempiu, su preigadu PrimeQ testat unu numeru cun riguardu a esser
issu primu: amentamus chi unu numeru intreu est primu si sos divisores suos funi issu e
totu e s'unidade:
PrimeQ[126]
False
PrimeQ[2^31-1]
True
Ateros preigados tenen riguardu si unu numeru est paris, disparis, o si un'imparis
de numeros est istruturadu in matrice o si est solu una lista e gasi a sighire:
{OddQ[21],EvenQ[21],MatrixQ[21],ListQ[{21}]}
{True, False, False, True}
1.8
Operadores logicos e relatzionales.Unu operadore relatzionale benit usadu po cunfrontare
duas espressiones e torrat unu valore True o False. Sos operadores relatzionales funi:
Equal(==),Unequal(!=),Greater(>),Less(<),GreaterEqual(>=) e LessEqual(<=). Sos
numenes inglesos funi sos numenes de sas funtziones e sos sinnos in parentis sa notatzione
infissa issoro. Cheren narrer e si lezzen eguale, diversu, majore, minore, majore o uguale
e minore o uguale. Si imprean po ponner numeros a cunfrontu:
7<5
False
3==7-4
True
Equal[3,7-4,6/2]
True
Si depet ponner attentzione a su fattu chi sos operadores relatzionale no tenen
precedentzia a respectu de sos operadores aritmeticos. E tando 3==7-4 enit interpretadu
gosie 3==(7-4) e non (3==7)-4.
Sos operadores logicos, connotos comente operadores booleanos cumponen frases de su
discursu, propositziones, de sas cales siat possibile chena farta narrer si issa funi
beras o fartzas. Funi operadores binarios e torran beru o fartzu cales resultadu de su
cumpostu basadu susu una aritmetica po s'appuntu booleana. Po esempiu, sa congiuntzione
intra duos custructos beros est semper bera:
7>1&&10>2
True
S'operadore booleanu And est rapresentadu cun &&. Una taula pitagorica,
una tabellina de And est sa chi sighit:
TableForm[
{{True&&True,True&&False},
{False&&True,False&&False}},
TableHeadings->{{T,F},{T,F}}]
T
F
T True False
F False False
Su operadore logicu Or si rapresentat cun || (sas barras verticales) : presentamus
esempios de s'impreu suu e posca sas tabellinas.
4==3||3==6/2
True
0==0||3==5
True
TableForm[
{{True||True,True||False},
{False||True,False||False}},
TableHeadings->{{T,F},{T,F}}]
T
F
T True True
F True False
Si ponzat attentzione a sa diferentzia de sinnificadu intra o de su limbazu comunu
e o chi rendet Or operadore booleanu. Una frase cale podet esser "est frittu o est
callente" impreat o in sensu esclusivu, est a narrer chi escludit sa possibilidade
chi unu ogettu siat in su matessi tempus frittu e callente. Su operadore logicu Or est
usadu in sensu inclusivu, e cheret narrer chi si A est beru e B est beru issu puru,tando
A||B est beru.
True||True
True
S'agatat unu operadore booleanu chi rendet su o esclusivu, si narat Xor, ma non
tenet indipendentzia ca podet esser esprimidu in termines de negatzione, Not(!) de Or e de
And: Xor=(x||y)&&!(x&&y) e cheret narrer tando o s'una o s'atera ma no
totu de duas.
TableForm[
{{(True||True)&&!(True&&True),
(True||False)&&!(True&&False)},
{(False||True)&&!(False&&True),
(False||False)&&!(False&&False)}},
TableHeadings->{{T,F},{T,F}}]
T
F
T False True
F True False
Ateros duos operadores funi s'implicatzione materiale, x implicat y, e sa
coimplicatzione, si est x tando est y.
x implicat y si rendet in termines de Not, Or e And in custa manera: !x||y e sa
coimplicatzione in cust'atera.(!x||y)&&(!y||x). Su lettore attentu e interessadu
hat a tenner contivitzu de si faer sos contos po contu suu. Custa est sa tabellina de sa
implicatzione materiale:
TableForm[
{{!True||True,!True||False},
{!False||True,!False||False}},
TableHeadings->{{T,F},{T,F}}]
T
F
T True False
F True True
E custa de sa doppia implicatzione:
TableForm[
{{(!True||True)&&(True||!True),
(!True||False)&&(True||!False)},
{(!False||True)&&(False||!True),
(!False||False)&&(False||!False)}},
TableHeadings->{{T,F},{T,F}}]
T
F
T True False
F False True
1.9
In sa idda mia sa passione po sos caddos b'est semper istada. In totus, o
cuasi, sas festas nois faghimos sas protzessiones a caddu. Bos potzo narrer de Santa Maria
de Sauccu ma s'istoria est longa meda. Tando, fintzas ca semus in tempus sou, bos conto
totu s'istoria de sas pariglias de carrasegare in bidda.
Prima, calchi deg'annos faghet las faghian d'onz'annu. Ma de cando si cche sun mortos sos
chi las faghian semper, sa traditzione s'est perdida. Si non fidi istadu po sos tzovanos
chi tenen passione, l'haimis perdida de su totu. Dae s'annu passadu l'han torrada a leare
mancari no bi sian bonos.
Ocannu gai e totu, han isterridu s'istrada a rena e po tres dies curren a pariglia. Sa
zente chi b'est acudida totu cuntenta, hat bantadu meda sos curridores comente esseran
cadderis de Siena. No est gai, ma su solu antu chi mi potho permitere de li dare est cussu
chi han torradu a leare custa traditzione e chi hana imbentadu carchi cosa po fagher biu
su carrasegare.
Lu naro fintzas si a mie sos caddos non mi sun mai piaghidos, ca los timo a frea. Pittitu
R.
Arrastos. Cando s'iscriet unu programma non semper totu andat po su versu suu, una
funtzione enit impreada meda po sighire arrastu de irballios, issa si narat Trace e
amustrat una lista de totu sos passos postos computande un'espressione. Usamus Trace in su
computu de un'espressione numerica:
Trace[(7*(3+1))/2]
1 1 7 4 4 7
{{3 + 1, 1 + 3, 4}, {-, -}, ---, ---, 14}
2 2 2 2
Nudda de su chi faet sa machina est diferente meda de comente s'irboligat unu
contu a pinna e paperi: a prima si calculat 3+1, su resultadu enit moltiplicadu po sette e
posca si dividit po duos: su resultadu finale est 14. Su calculadore sighit sa matessi
logica chi s'imparat in ischola.
Una funtzione simbitzante meda a Trace est TracePrint, e carchi orta sas arrespostas suas
resultan prus craras:
TracePrint[(7*(3+1))/2]
7 (3 + 1)
---------
2
Times
7
3 + 1
Plus
3
1
1 + 3
4
1
-
2
Power
2
-1
1
-
2
Rational
1
2
7 4
---
2
4 7
---
2
14
14
1.10
Cantu lestresa. Unu poder haer disizu de ischire in cantu
tempus si faet unu contu, e sa cosa podet esser fatta cun sa funtzione Timing. Ponimus de
cherrer ischire in cantu tempus unu numeru mannu enit fattorizadu, po narrer chentu
fattoriale: 100!
Timing[FactorInteger[100!];]
{0. Second, Null}
Unu faer de rughe! Cando unu computu est istadu giai fattu, su
tempus sinnaladu est cussu chi enit impreadu a letzer sos registros de memoria. Su
programma no irmentigat mai nudda.
Timing[FactorInteger[100!];]
{0. Second, Null}
Timing est una aliaga po ischire cantu lestra est una funtzione o unu algoritmu.
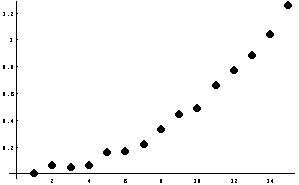
Est cosa pacifica chi a fattorizare sos numeros est unu protzessu chi arrechedit tempus
meda, e custu aumentat in manera esponentziale a manu a manu chi sos numeros creschen de
valore. Amustramus ite sutzedit realmente, e nde pesamus unu graficu:
tempusimpreadu:=
Table[
Timing[
FactorInteger[(100 j)!]][[1]],{j,1,15}]
ListPlot[
tempusimpreadu/Second,
PlotStyle->PointSize[0.02]];