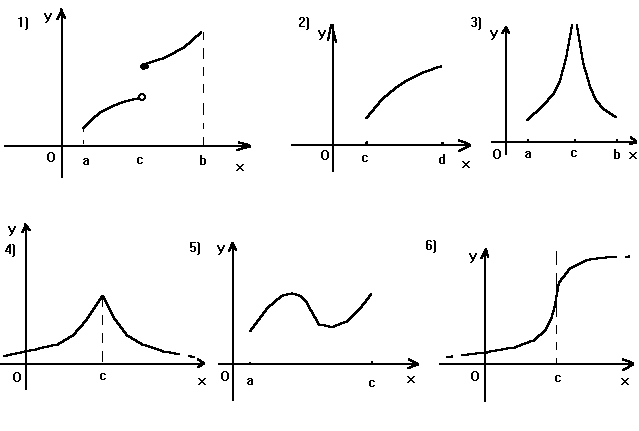PREREQUISITI : concetti di insieme, relazione, intervallo, intorno, quantificatori, Riferimento Cartesiano Ortogonale (RCO), le coniche, funzioni, operazioni e composizioni di funzioni.

DEFINIZIONE : Sia f :  ®  una relazione di dominio  e codominio  ;

f : A Í Â ® Â e' una funzione se " aÎ A $ ! b Î Â b = f(a)

a e' detta variabile indipendente e b variabile dipendente

A e' detto campo di esistenza o insieme naturale di definizione della funzione

D'ora in poi considereremo solo funzioni definite in un insieme A che sia un intervallo o unione di intervalli.

In alcuni casi e' interessante considerare anche l'insieme Á dei valori che assume la f in  .

Il grafico di una funzione e' l'insieme

G º {(x, f(x)) Î Â 2 / x Î A, f(x) Î Á }

La rappresentazione grafica di tale insieme in un R.C.O. e' detta "curva di equazione y = f(x)"

ESEMPIO : Y = 2x - 3 f : Â ® Â x ® 2x - 3

questa e' chiaramente una funzione: ad ogni valore di x resta associato uno e un solo valore di y. Il suo grafico e' rappresentato da una retta

ESERCIZI

1) Osserva attentamente i seguenti grafici e stabilisci quali di essi sono grafici di funzioni e quali no e, in caso affermativo, stabilisci anche l'insieme di definizione e l'insieme delle immagini.

Cerca ora di giustificare le tue risposte

2) Date le seguenti funzioni, attribuisci alla variabile indipendente alcuni valori e calcolane i valori corrispondenti (per via algebrica).

Trova campo di esistenza (C.E.) e insieme delle immagini della funzione data. Rappresenta graficamente la funzione e ritrova sul grafico le ordinate corrispondenti ai valori attribuiti alla x.

a) y = -x + 4 b) y = c) y = 3x + 2

d) 3x + 6y - 1 = 0 e) 4x - y = 0 f) x = -3y + 1

g) y = h) y = - i) xy = 6

l) xy = -2 m) y = x 2 n) y = x 2 + 1

o) y = -x 2 +2 p) y = q) y = x 2 + x

r) y = x 2 - x + 1 s) y = -x 2 + 3x t) y = -x 2 + 2x - 3

u) y = (x - 1)2 v) y = z) y =

1) y = 2) y = 3) y =

4) y = 5) y = sen x 6) y = cos x

7) y = tg x 8) y = log2 x 9) y = ln x

10) y = 11) y = 12) y =

13) y = 14) y = | x| 15) y =

16) y = 17) y = 18) y =

19) y = 20) y = 21) y =

22) y = 23) y = 24) y =

25) y = 26) y = 27) y = 2 sen x

28) y = 3 cos x 29) y = sen 2x 30) y = cos 2x

31) y = 32) y = tg 3x 33) y =

34) y = -2 cos 3x 35) y = ) 36) y =

37) y = 38) y = | sen 2x| 39) y = sen | x|

40) y = 2 | cos x| 41) y = 42) y = | tg 2x|

43) y = -| cos | x| | 44) y = ln | x| 45) y = 2 ln x

46) y = ln x 2 47) y= 48) y =

3) Stabilisci, "leggendone" il grafico, quali delle seguenti equazioni rappresentano funzioni. In caso affermativo individua il Campo di Esistenza e l'Insieme delle immagini.

1) y = 2) y =

3) y = 4) y =

5) y =

Consideriamo ora il segno di una funzione

L'insieme di POSITIVITÀ di una funzione f : A Í Â ® Â e'

P = { x Î A : f(x) > 0 }

L'insieme di NEGATIVITÀ e'

N = { x Î A : f(x) < 0 }

L'insieme degli ZERI e'

Z = { x Î A : f(x) = 0 }

ESERCIZI

4) Considera la funzione y = x + 3 . Completa la seguente tabella e rappresentala graficamente:

Per quali valori di x della tabella la y e' positiva? negativa? nulla?

In generale, per quali valori di x la y e' positiva? Puoi procedere nel seguente modo

y = x + 3 y > 0 Þ x + 3 > 0 Þ x > - 3

P º { x > 3 }

dove e' negativa?

dove e' nulla?

5) Riprendi le equazioni dell'esercizio 3) e stabilisci per quali valori di x la y e' >, =, < 0.

6) Prendi in considerazione i grafici disegnati nel primo esercizio e deduci da essi P, N, Z delle funzioni rappresentate.

DEFINIZIONE : Data una funzione y=f(x) e dato x° appartenente al suo dominio A, diremo che la funzione ha in x° un punto di Massimo (Minimo) Assoluto se " xÎ A f(x°)³ f(x) ( f(x°)£ f(x) ).

ESERCIZI

7) Delle funzioni riportate negli es. 2) - 3) definisci i Massimi e i Minimi, se esistono.

Disegnamo ora la parabola di equazione

y =

completa la tabella sotto riportata

Osserva ora la tabella : all'aumentare dei valori che assume la variabile x cosa succede ai corrispondenti valore della variabile y?

0 < 1 allora f(0) ............ f(1)

4 < 5 f(4) ............ f(5)

In generale

se x £ 3 all'aumentare di x la y diminuisce, mentre

se x ³ 3 all'aumentare di x la y aumenta

Diremo anche che

per x £ 3 la funzione e' DECRESCENTE

per x ³ 3 la funzione e' CRESCENTE

DEFINIZIONE : Data la funzione f : A Í Â ® Â essa e' CRESCENTE nell'intervallo I Í A se

essa e' DECRESCENTE nell'intervallo I Í A se

Se I º A la funzione e' crescente o decrescente in tutto il Campo di Esistenza ( si dice che e' globalmente crescente o globalmente decrescente)

ESEMPIO:

Osservando il grafico si può' osservare che

in [-2 , 0] la funzione e' crescente

in [0 , 2] la funzione e' decrescente

in [2 , 5] la funzione e' crescente

ESERCIZI

8) Osserva i seguenti grafici e stabilisci gli intervalli di crescenza e decrescenza delle funzioni rappresentate

9) Osserva il seguente grafico

Puoi ancora dire che la funzione rappresentata e' crescente nell'intervallo [-3 , 8]?

10) Osserva ora il seguente grafico

Puoi dire che la funzione e' decrescente nell'intervallo [ -4 , 7]?

Quali sono i valori di x per i quali non "funziona" la definizione di crescenza o decrescenza in un intervallo?

Per poter descrivere situazioni come queste occorre una nuova definizione :

DEFINIZIONE : Data la funzione f : A Í Â ® Â essa e'

NON DECRESCENTE (o crescente debolmente) nell'intervallo I Í A se

NON CRESCENTE (o decrescente debolmente) nell'intervallo I Í A se

DEFINIZIONE : Una funzione crescente o decrescente in senso stretto o in senso debole si dice MONOTONA

ESERCIZI

11) Osserva i seguenti grafici e stabilisci quali funzioni sono crescenti, decrescenti, non crescenti e non decrescenti nel loro insieme di definizione.

12) Prendi i grafici del primo esercizio e stabilisci (anche approssimativamente) gli intervalli di crescenza, decrescenza, non crescenza, non decrescenza.

Sia f : A Í Â ® Â e x0 Î A (interno ad A, cioè tale che esisteno x1 , x2Î A tali che x1 < x0 < x2 )

DEFINIZIONE : Si dice che f e' crescente in x0 se

DEFINIZIONE : Si dice che f e' decrescente in x0 se

Si parlerà' di non crescenza o non decrescenza se le disuguaglianze valgono in senso debole cioè' se

ESERCIZI

13 Riprendi in considerazione la curva di equazione y = .

In x = 4 la funzione e' crescente o decrescente?

14) Osserva i seguenti grafici e stabilisci se nel punto c la funzione e' crescente o decrescente.

Costruiamo ora il grafico della funzione f : Â ® Â x® cioè'

La funzione ha minimo assoluto (m = 0) nei punti x = 1 e x = 5, non ha massimo assoluto.

Osserva pero' cosa accade in x = 3. Se restringiamo il campo di indagine ad un intervallo sufficientemente piccolo, ad esempio [2 , 4], la funzione assume valore massimo (M = 4) per x = 3.

Allora

DEFINIZIONE : la funzione y = f(x) assume MASSIMO RELATIVO nel punto x = x0 se

Analogamente la funzione y = f(x) assume MINIMO RELATIVO nel punto x = x0 se

ESERCIZI

15)Individua nei grafici dell'esercizio 8 i punti di MINIMO RELATIVO, ove esistano

16) Osserva i seguenti grafici e stabilisci se ci sono punti di MASSIMO e di MINIMO RELATIVO.

I punti di massimo e di minimo relativo si dicono anche "estremi relativi" o "punti estremanti". Si può' anche vedere facilmente che se x0 e' punto di massimo relativo per y = f(x), allora la funzione e'non decrescente in un intorno sinistro di x0 e decrescente in un intorno destro, mentre se x0 e' punto di minimo relativo, la funzione e' non crescente in un intorno sinistro e crescente in un intorno destro di x0.

Sia f : A Í Â ® Â .

DEFINIZIONE : y=f(x) e' CONCAVA VERSO L'ALTO se per ogni coppia di punti , la corda congiungente i punti "sta al di sopra" (o per lo meno "non sta al di sotto") del grafico della funzione y=f(x).

[In altre parole " a Î Â con 0 £ a £ 1 si ha ]

DEFINIZIONE : f(x) e' CONCAVA VERSO IL BASSO se per ogni coppia di punti , la corda congiungente i punti "sta al di sotto" (o per lo meno "non sta al di sopra") della funzione f(x).

[Cioè' " a Î Â con 0 £ a £ 1 si ha ]

ESERCIZI

17)Stabilisci quali dei seguenti grafici rappresenta una funzione concava verso l'alto o quali verso il basso.

Ti sarai accorto che alcune funzioni rappresentate non sono ne' concave verso il basso ne' verso l'alto. Si può' pero' dare una definizione LOCALE di concavita':

DEFINIZIONE : f(x) e' concava verso l'alto in un intervallo I Í A se per ogni coppia di punti , la corda congiungente i punti sta al di sopra (o per lo meno non sta al di sotto) della funzione f(x).

DEFINIZIONE : f(x) e' concava verso il basso in un intervallo I Í A se per ogni coppia di punti , la corda congiungente i punti sta al di sotto (o per lo meno non sta al di sopra) della funzione f(x).

ESERCIZI

18) Nei seguenti grafici stabilisci gli intervalli di concavità' verso l'alto e verso il basso.