|
PARTE SECONDA
I LIMITI Introduzione intuitiva al concetto di limite
Consideriamo la funzione f: x ® x² il cui grafico ti è certamente noto:
Possiamo anche determinare il valore della funzione in alcuni punti
Per determinare sul grafico il punto di coordinate ( 106 , 1012 ) avvresti bisogno di un foglio enorme o dovresti scegliere unità di misura così microscopiche da non poter individuare altri punti. Dal grafico e dalla tabella numerica si intuisce che, al crescere, in valore assoluto, dei valori della x valori corrispondenti della y crescono indefinitamente. In matematica si sintetizzano frasi di questo tipo con la scrittura
( si legge: il limite per x che tende a più infinito di x² è uguale a più infinito)
Il simbolo "+ ¥ " [-¥ ] non è un numero reale, ma traduce l’idea che la funzione assume valori sempre più grandi (positivi o negativi).
Costruiamo per punti, approssimativamente, il grafico di y = :
Si intuisce che, quando i valori della x tendono a zero, sia per valori approssimanti per eccesso ( da destra, oppure 0+) che per difetto (da sinistra, oppure 0-) i valori della y diventano indefinitamente molto molto grandi. Brevemente
Si può costruire il grafico approssimativo della funzione
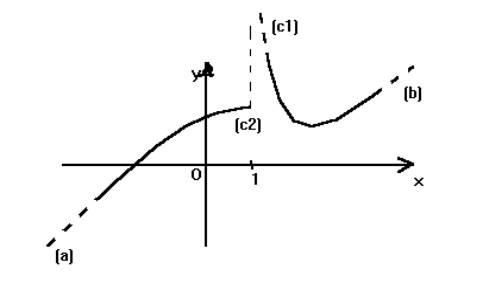
Consideriamo il seguente grafico e proviamo ad interpretarlo utilizzando la nuova "stenografia" introdotta:
Possiamo tradurre le seguenti situazioni: a) c) In genere utilizziamo queste "scritture" per evidenziare il comportamento della funzione nelle "vicinanze" degli estremi degli intervalli che ne determinano il campo di esistenza. Nota in particolare che relativamente al caso c2 si ha anche f(1)=2. ESERCIZI 19) Utilizzando il grafico seguente dedurne i limiti richiesti:
a) b) c) 20) Ripetere l'esercizio precedente:
a) b) c)
21)Come sopra
a) b) 22)Come sopra
a) b) c) 23)Come sopra
a) b)
c) Avrebbero senso le scritture
24) Interpreta utilizzando i limiti i seguenti grafici: a) b)
c) d)
e) f)
25) Quali delle seguenti scritture sono corrette per ciascun grafico assegnato?

1) 2)
3) 4) 5) 26) Considera le seguenti funzioni e determinane il dominio. Con l'uso della calcolatrice e del grafico deducine il comportamento agli estremi degli intervalli che ne determinano il campo di esistenza. a) y = log½x b) y = 3x c) y = 3-x d) y = x² e) y = 4-x² f) y = g) y = h) y = tgx con -p/2<x<p/2 i) y = cotgx con 0<x<p l) y = senx m) y = cosx n) y = arctgx o) y = arccotgx p) y = log3|x| q) y = |log1/3x| r) y = 2|x| s) y = t) y = u) y = |x| v) y = 27)Noto il grafico della funzione f : x® f(x) dedurre: dominio e insieme delle immagini, intersezione con gli assi, positività e negatività, crescenza e decrescenza, massimi e minimi, concavità. Dedurne, inoltre, il comportamento agli estremi degli intervalli che ne determinano il campo di esistenza. a) d) g) 
28) Dedurre il grafico della funzione f : x® f(x) noto che: a) è definita su tutto  interseca gli assi nel punto (0,0) è positiva per x ¹ 0 cresce per 0<x<2 decrese per x<0 È x>2 è concava verso l'alto per x < 2-Ö 2 È x > 2+Ö 2 e verso il basso per 2-Ö 2< x <2+Ö 2 ha un massimo relativo in M(2,1) e un minimo assoluto in m(0,0) valgono b) è definita per x ¹ ±1 ed è dispari interseca gli assi coordinati nel punto (0,0) è positiva per -1< x <0 È x >1 è negativa per x <-1 È 0 < x <1 decresce per ogni x Î D non ha nè massimi nè minimi è concava verso il basso per x <-1 È 0 < x <1 è concava verso l'alto per -1< x <0 È x >1 valgono
c) è definita per x <1 v x >2 interseca gli assi coordinati nei punti A(-2,0), B(0,-4), C(3,0) è positiva per x<-2 v x>3 è negativa per -2<x<1 v 2<x<3 cresce per x>2 e decresce per x<1 non ha nè massimi nè minimi ed è sempre concava verso il basso valgono
d) è definita per ogni x Î Â ed è pari interseca gli assi nel punto (0,0) è positiva per x ¹ 0 cresce per x<Ö 3 È 0<x<Ö 3 decresce per Ö 3<x<0 È x>Ö 3 ha massimi nei punti (Ö 3,3) e (Ö 3,3), minimo in (0,0) è concava verso l'alto per x<-4 È x>4 e verso il basso per -4<x<4 valgono
CONFRONTO FRA INFINITI E INFINITESIMI
Costruiamo per punti, in uno stesso R.C.O. Monometrico i grafici delle seguenti funzioni, ristrette all'intervallo [0,+¥ ).
y=x
y=x2
y=x3
Osserviamo che:
I limiti di tutte le funzioni considerate per x che tende a +¥ , sono uguali a +¥ , ma, dai grafici, si intuisce che alcune raggiungono valori "molto grandi" più rapidamente di altre. Possiamo quindi stilare una specie di "graduatoria" di infiniti. In generale, considerata y = xn con n Î Q+ e x tendente a +¥ , al crescere di n ci troviamo in presenza di infiniti "più rapidi": n è detto ordine di infinito. Conosci però altre funzioni che tendono all'infinito per x tendente a +¥ e precisamente y = loga x e y = ax con a>1. Studiamo in particolare y = lnx e proviamo a confrontarla ad esempio con y = x y = Ö x y = 7Ö x Costruiamo in uno stesso R.C.O.M. i relativi grafici dopo aver completato le seguenti tabelle: y=lnx
y=x
y=Ö x
y=7Ö x
Si vede chiaramente che y = ln x è un infinito più debole di y = x e y = Ö x, ma si intuisce anche, dalla tabella, che è più debole di y = 7Ö x in quanto, per valori molto molto grandi,la funzione y=7Ö x assume valori superiori a ln x. Si può dimostrare che ln x è un infinito più debole di qualunque potenza di x; in simboli
Questo sintetizza il fatto che pes ogni nÎ Q+ il denominatore, per x tendente a +¥ , "vince" il confronto con il numeratore. La stessa cosa si può dimostrare per logax con a>1, per cui in generale si dice che il logaritmo (con base maggiore di 1), ha ordine di infinito minore di ciascuna potenza razionale positiva di x. Formalmente
Procediamo in modo analogo per la funzione esponenziale
y = x
Si puo' notare che la funzione esponenziale e' un infinito di ordine superiore a qualunque potenza di x, in simboli
Si dimostra che, in generale,
Confronti analoghi a prima si possono fare quando si hanno funzioni tali che
y = x
Stavolta nelle tabelle prendiamo in considerazione valori prossimi a 0. Si intuisce che al crescere di n, cresce la "velocita'" di avvicinamento a 0; n si dice ordine di infinitesimo. Consideriamo ora la funzione sin x, che per x® 0 e' un infinitesimo. y = sin x
y = x
Si puo' notare che sin x e x hanno nelle immediate vicinanze do 0 lo stesso comportamento, in simboli
In modo analogo si ha
Si dice che le funzioni sin x e tg x sono infinitesimi del 1° ordine, o in altre parole che, nelle vicinanze dell'origine, si possono approssimare con la funzione x sin x » x tg x » x in un intorno di (0) Consideriamo ora la funzione
y = x
Si puo' notare che y = In generale, si dice che una funzione y=f(x) e' un
infinito per x® a, quando ed e' un infinitesimo per x®
a quando Anche in tal caso si puo' stabilirne l'ordine di
infinito o infinitesimo confrontandole rispettivamente con
|


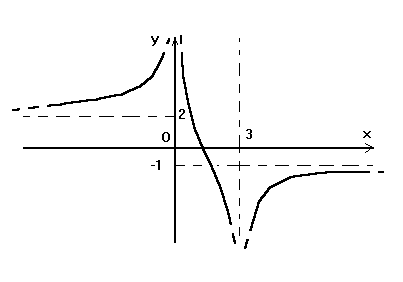










 b)
b)
 c)
c) 
 e)
e)
 f)
f)
 h)
h)
 i)
i) 

