L'infinito
in
Matematica
“Da
tempo immemorabile l’infinito ha suscitato le passioni umane più di ogni altra
questione. E’ difficile trovare un’idea che abbia stimolato la mente in modo
altrettanto fruttuoso, tuttavia nessun altro concetto
ha più bisogno di chiarificazione” (D. Hilbert).
Quello
che segue è un tentativo di esaminare il concetto matematico di infinito affrontando la
sua storia “per problemi”.
I
numeri naturali
E’
a partire dai numeri naturali e dai loro rapporti che si è sviluppata nel tempo la
Matematica, e per questo vale la pena di cominciare questa riflessione analizzando quale
concetto di infinito è connesso con questi enti matematici
La
successione crescente dei numeri naturali non ha fine, è infinita perché fissato comunque un numero naturale è sempre possibile
trovare un numero maggiore di esso.
E’
una infinità inesauribile che si ottiene aggiungendo sempre ‘uno’
all’ultimo numero determinato; tale tipo di infinito potenziale viene chiamato infinito per aggiunzione. La definizione di
infinito potenziale per una successione di elementi è appunto questa: è la possibilità
di procedere sempre oltre senza che ci sia un elemento ultimo.
Si
osservi che un infinito pensato come un processo per successive aggiunzioni, è ciò che
si pone sempre all’esterno di quello che è già stato unificato
dall’intuizione. Kant chiamava “progressus in indefinitum” l’infinito per aggiunzione che non ammette
nessuna limitazione se non quella provvisoria che gli può essere assegnata ad ogni suo
passo, prima di procedere al passo successivo.
Se
immaginiamo di rappresentare graficamente la successione dei numeri naturali , dovremmo
raffigurare una serie di punti separati (ed equidistanti) che si susseguono senza fine
perché sarà sempre possibile aggiungerne ancora uno. Si tratta di una successione
infinita discreta: fatto un passo è ben chiaro
quale deve essere il successivo, tra due elementi consecutivi c’è uno stacco netto,
c’è il “vuoto”.
“Tutto
sommato”, afferma L. Lombardo Radice, “una successione infinita discreta, sempre
riconducibile alla ripetizione infinita del ‘più un altro’ è un oggetto
mentale di tutto riposo “; Hegel chiamava questa prima e più elementare
manifestazione delll’ infinito potenziale “la cattiva o mala infinità”.
I
numeri razionali
Ma
l’infinito potenziale può manifestarsi in forme meno elementari come nel caso dei
numeri razionali. Infatti l’insieme dei numeri razionali non è un insieme discreto,
esso è invece denso: tra due numeri razionali,
per quanto vicini, ce ne sono infiniti maggiori del più piccolo e minori del più grande;
ad esempio, sono infiniti i numeri razionali compresi tra 0 ed 1: sono tutte le frazioni
che hanno il numeratore più piccolo del denominatore.
Se
poi consideriamo, il segmento di estremi 0 ed 1 ed associamo ogni frazione tra essi
compresa ad un punto di tale segmento, possiamo
osservare che tali frazioni rappresentano infinite divisioni
del suddetto segmento.
L’infinito
potenziale espresso dai numeri razionali è perciò un infinito ottenuto per divisione; la caratteristica di tale infinito, che Kant
chiamava “regressus in infinitum”, è
che esso è interamente contenuto in una totalità limitata: dividendo all’infinito
un segmento in parti sempre più piccole, risulta
evidente che tutti gli elementi della divisione sono in realtà già assegnati e presenti,
prima ancora che la stessa divisione abbia inizio; appartenendo ad una forma limitata essi
non possono sfuggire e non possono che essere ritrovati durante un processo
all’infinito che inevitabilmente il raggiunge tutti.
La
differenza tra “progressus in indefinitum” e “regressus in infinitum”
secondo Kant sta proprio in questo: nel primo caso gli elementi vanno cercati al di fuori della totalità parziale,
sempre finita, che non si cessa mai di ottenere; nel secondo essi vanno trovati in un tutto preesistente.
La
matamatica greca e l’infinito
Il
concetto di infinito è stato elaborato dalla filosofia greca con valenze prevalentemente
negative (come si può notare anche dalla parola che lo definisce nelle varie lingue: a-peion in greco, in-finitum in latino, un-endlich in tedesco, ecc.) ed è stato dalla
stessa accettato solo come divenire, quindi come
infinito potenziale rifiutando pertanto l’idea di un infinito attuale. Lo stesso
Aristotele affermava che “... il numero è infinito in potenza, ma non in atto. [...]
questo nostro discorso non intende sopprimere per nulla le ricerche dei matematici per il
fatto che esso esclude che l’infinito per accrescimento sia tale da poter essere
percorso in atto. In realtà essi, stessi allo stato presente, non sentono il bisogno dell’infinito ( e in
realtà non se ne servono), ma soltanto di una quantità grande quanto essi vogliono, ma
pur sempre finita [...]”.
Il
rifiuto dell’infinito attuale nasce dal fatto che i greci ritenevano conoscibile solo
ciò che è determinato, finito; tutto ciò che è indeterminato, infinito e perciò
inconoscibile è quindi da rifiutare al punto che non solo viene respinta l’idea
dell’infinito attuale, ma si accetta l’infinito potenziale solo come processo di ecceterazione, cioè come possibilità
di procedere sempre oltre, un passo alla volta, ottenendo ad ogni passo quantità sempre
più grandi, ma comunque finite.
Anche
la matematica greca: Euclide, Pitagora, Archimede e tutti i grandi matematici di quel
tempo rifiutarono ovviamente l’infinito attuale, ritenendo lecita solo la concezione
dell’infinito come divenire. Su diversi fronti della matematica, tuttavia, questa
concezione dell’infinito entrò in crisi, suscitando dei problemi spesso
insormontabili per i matematici del tempo e creando i presupposti per il superamento della
stessa, superamento che inizierà a partire dai primi decenni del seicento ad opera di
Galileo Galilei.
Ci
soffermiamo ora proprio su tre gandi problemi che misero in crisi i matematici greci ed il
loro modo di concepire l’infinito: la scoperta dei segmenti incommensurabili, i
paradossi di Zenone (prenderemo in considerazione il più famoso: Achille e la tartaruga),
la rettificazione della circonferenza.
Pitagora
e i segmenti incommensurabili
Uno
dei dogmi del pitagorismo era stata la concezione secondo cui l’essenza di tutte le
cose, sia in geometria, sia nelle questioni pratiche e teoriche della vita umana era
spiegabile in termini di arithoms, cioè di
proprietà intrinseche dei numeri interi e dei loro rapporti. Essi credevano che i corpi
fossero costituiti di corpuscoli tutti uguali tra loro e disposti in forme geometriche.
Questa convinzione in ambito geometrico portava a ritenere che anche i punti avessero
un’estensione (sia pure piccolissima). Da ciò essi deducevano che un segmento
dovesse essere formato da un numero finito di punti.
Pertanto il rapporto di due segmenti doveva risultare uguale al rapporto di numeri interi
che esprimevano quante volte il punto era contenuto in ciascuno dei due segmenti. In altre
parole essi pensavano che il punto fosse il sottomultiplo
comune a tutti i segmenti; cioè che tutti i segmenti fossero tra loro commensurabili ( Def: due grandezze omogenee si
dicono commensurabili quando ammettono una grandezza omogenea alle prime due che è
contenuta un numero intero di volte in ciascuna di esse).
Applicando
il Teorema di Pitagora al triangolo rettangolo isoscele essi furono però costretti ad
ammettere l’esistenza di grandezze incommensurabili:
scoprirono infatti l’incommensurabilità della diagonale del quadrato rispetto ad un
suo lato.
Detti
l e d
il lato e la diagonale di un quadrato supponiamo per assurdo che essi siano commensurabili
cioè che il loro rapporto l/d sia
esprimibile mediante una frazione p/q con p e q
numeri interi.
Per il Teorema di Pitegora è
d2
= l2+l2 da
cui d2/l2 = 2l2/l2
= 2 ma è anche d2/l2
= p2/q2 da
cui p2/q2 = 2 cioè
(*) p2 =
2q2
ma
allora p2 è pari e contiene il fattore 2 un numero pari di
volte (è elevato al quadrato), mentre 2q2 contiene
il fattore 2 un numero dispari di volte (indipendentemente dal fatto che q sia pari o dispari); è quindi assurdo supporre
vera la (*) e l’assurdo nasce
dall’aver supposto d e l commensurabili.
Ma
se d ed l sono incommensurabili, cosa succede se si
tenta di determinare il rapporto l/d?
Riportando
sulla diagonale prima l, poi 1/10 l, poi 1/100 l,...
si ha:
l<d; 1,4 l<d; 1,41 l<d; ...
e
così via all’infinito; cioè il rapporto
tra grandezze incommensurabili è espresso mediante un numero decimale illimitato
aperiodico (se fosse periodico sarebbe riducibile a frazione) che viene chiamato numero irrazionale.
L’esistenza
di grandezze incommensurabili e conseguentemente dei numeri irrazionali contraddiceva non solo le convinzioni filosofiche
dei pitagorici, ma metteva anche in crisi il concetto di infinito della filosofia greca;
non c’è da meravigliarsi perciò del fatto che fu proibito ai membri della setta di
rivelare ad altri queste scoperte considerate blasfeme e sconcertanti.
Il
numero irrazionale, inoltre, sembrava contraddire la verità per cui nulla esiste se non
ciò che è attuale, infatti, pur sembrando sprovvisto di un’esistenza attuale (non
può essere esibito come l’insieme di “tutte” le sue cifre), esso
rappresenta indubbiamente “qualcosa”.
Achille
e la Tartaruga
Uno
dei più famosi paradossi dell’infinito potenziale è quello di “Achille e la
tartaruga” in cui Zenone di Elea (500 a.C.) sembra dimostrare l’impossibilità
del moto.
Supponiamo
che Achille sia due volte più veloce della tartaruga e che entrambi gareggino lungo un
percorso di un metro. Supponiamo inoltre che Achille dia mezzo metro di vantaggio alla
tartaruga.
Quando
Achille avrà percorso mezzo metro, la
tartaruga si troverà più avanti di Achille di un
quarto di metro; quando Achille avrà percorso quel quarto, la tartaruga si troverà
avanti di un ottavo di metro e così via all’infinito
cioè Achille non raggiungerà mai la tartaruga.
Se
osserviamo il percorso di Achille troviamo che esso è dato da infiniti tratti che
costituiscono la successione
1/2 ;
1/2 + 1/4 = 3/4; 3/4
+ 1/8 = 7/8; 7/8 + 1/16 =
15/16; ... ;
(2n - 1)/2n
ed
è facile osservare che questa successione tende a 1. Vediamo così che una somma di quantità
finite in un numero illimitato non è
necessariamente finita.
D’altro
canto i tratti di strada percorsi da Achille nel tentativo di raggiungere la tartaruga
sono dati dalla succesione
1/2;
1/4; 1/8; 1/16;
... ; 1/2n
ed
anche questa successione tende a 1.
Cosa
significa però l’espressione “tende a 1”?
Significa
che se chiamo sn la somma dei primi n tratti percorsi da Achille allora sn , per quanto grande sia n , non supera mai 1, numero al quale si avvicina sempre di più.
Sempre
più, anzi quanto
si vuole: la differenza tra 1 ed sn , per n opportunamente grande, si fa più piccola di un
qualsiasi numero per quanto piccolo da noi scelto.
E’
questa una proprietà caratteristica del Limite
definito nell’Ottocento da Weierstrass.
Con
la nozione matematica di limite si può dunque disporre della soluzione del paradosso
infatti, pur conservando l’idea di un processo e di una potenzialità illimitata, il
limite ha il potere di risolvere tale potenzialità in una unità formale.
E’
perciò possibile esprimere concretamente la soluzione finale di un processo illimitato
senza rinunciare al carattere potenziale di quest’ultimo: l’inesauribilità di
questo processo resta un fatto irrinunciabile, ma non per questo dobbiamo accontentarci di
soluzioni approssimate. Il valore 1 è un
limite che “comprende” tutta la successione
(2n - 1)/2n , è una soluzione della
potenzialità di sviluppo di tale successione, pur mantenendosi sempre al di fuori di
questa.
La
rettificazione della circonferenza
Il
problema della rettificazione della circonferenza, cioè di riuscire a calcolare la
lunghezza della circonferenza, ha appassionato molti eminenti filosofi dell’antica
Grecia, Questo problema venne risolto in modo soddisfacente e non contraddittorio rispetto
alle convinzioni del tempo da Eudosso di Cnido (400 - 350 a.C.). Mediante il
“suo” Metodo di esaustione egli
infatti fornì il lemma che costituisce la base di tale metodo: date due grandezze aventi
un certo rapporto (cioè nessuna delle quali sia zero) è possibile trovare un multiplo
dell’una che superi l’altra.
I
matematici precedenti avevano suggerito di risolvere il problema inscrivendo e
circoscrivendo alla circonferenza dei poligoni aventi un numero di lati sempre crescente;
in tal modo ogni lato si approssima sempre di più all’arco di circonferenza sotteso
e il perimetro dei poligoni si approssima alla misura della circonferenza.
Nasceva
però a questo punto un problema: è possibile sostenere che “alla fine“ i
poligoni si identificheranno con la circonferenza e che i rispettivi lati potranno essere
considerati archi “infinitesimali” della stessa?
Antifonte
affermava che questo era possibile, ma così facendo confutava il concetto di infinito
come infinito potenziale contraddicendo così il pensiero di Aristotele: le asserzioni di
Antifonte portavano infatti a considerare la circonferenza come un poligono con un numero
infinito di lati e ad accettare perciò la stessa come un infinito attuale. Aristotele
ovviamente contestò le affermazioni di Antifonte: egli affermò infatti che
l’insieme dei poligoni inscritti (e circoscritti) nella circonferenza è un insieme
illimitato nel senso che per ogni poligono con un numero comunque elevato di lati ne
esisterà un altro con un numero di lati ancor più elevato che non potrà coincidere con
la circonferenza perché ammetterà dopo di se’ un ulteriore poligono con un numero
di lati ancora maggiore ... riproponendo quindi il concetto di infinito come processo di
ecceterazione e quindi come infinito potenziale.
Come
precedentemente detto il problema della rettificazione della circonferenza poté essere
risolto solo grazie al Lemma di Eudosso, mediante una reductio ad absurdum (provando che il risultato non può non essere quello, si dimostra infatti,
poiché due negazioni affermano, che deve
necessariamente essere quello).
Supponiamo
infatti che la lunghezza C della circonferenza di raggio r non
sia 2pr,
ma sia un numero più piccolo cioè
(1 )
C
< 2pr
Ma
allora per il Lemma di Eudosso è possibile trovare un poligono inscritto nella
circonferenza con un numero sufficientemente grande di lati, il perimetro del quale,
certamente minore della circonferenza, ha misura maggiore di C .
Supponiamo
al contrario
(2 ) C > 2pr
ma
allora è possibile, analogamente a quanto visto prima, trovare un poligono circoscritto
alla circonferenza il cui perimetro è minore di C.
essendo
perciò assurdo supporre sia (1 ) che (2) non resta che affermare
che
C
= 2pr
“Questo
procedimento ineccepibile dal punto di vista logico-formale non è altro che il panno
logico con il quale l’infinito potenziale nasconde le vergogne dell’infinito
attuale. E’ qui evidente un problema fondamentale risolto da Cantor
nell’Ottocento: è possibile solo una suddivisione
del continuo in un numero quanto si voglia grande di parti, solo una infinità
potenziale di suddivisioni, oppure si può pensare il continuo come una infinità in atto di componenti ultime, altissime,
indivisibili?” (L. Lombardo Radice).
Galilei
e l’infinito
Il
primo a mettere in discussione il concetto di infinito così come era stato elaborato
dalla filosofia greca fu Galileo Galilei. Egli affermò la possibilità di ridurre un
continuo limitato (ad esempio un segmento) in infiniti elementi “primi” non
“quanti” (cioè senza estensione), indivisibili. Poiché infatti un segmento
può essere diviso in quante si vuole parti ancora divisibili, si deve necessariamente
ammettere che esso sia composto da infinite parti, ma se queste parti sono infinite allora
devono necessariamente essere “non quante”, cioè prive di estensione, perché
infinite parti estese hanno un’estensione infinita, mentre il segmento ha
un’estensione limitata.
L’infinito
in atto, allora, non può non essere pensato ed il segmento non è altro che una sua
manifestazione. Un’altra espressione dell’infinito attuale è allora la
circonferenza: poiché infatti è possibile “piegare” un segmento a formare un
quadrato o un qualunque poligono regolare con un qualsivoglia numero di lati, allora
piegandolo a formare un cerchio si può benissimo dire di “aver ridotto all’atto
quelle parti infinite che prima, quando era un segmento dicevamo esser di lei contenute in
potenza”. Possiamo infatti “vedere” la circonferenza come un poligono con
un numero infinito di lati.
Galilei
fu però anche il primo a rendersi conto dei paradossi che nascevano dall’ammettere
l’infinito attuale e per questo, pur affermando con forza le sue idee sul piano
filosofico, preferì essere più cauto dal punto di vista matematico, rifiutando di
utilizzare gli “infiniti indivisibili non quanti” in geometria: egli elaborò
infatti dei paradossi che non riuscì a risolvere e questo lo portò ad affermare che
“Queste son di quelle difficoltà che derivano dal discorrer che noi facciamo col
nostro intelletto finito intorno a gl’infiniti, dandogli quelli attributi che noi
diamo alle cose finite e terminate; il che penso che sia inconveniente...”.
I
paradossi proposti da Galilei che qui consideriamo sono due: Il Paradosso dei quadrati e
il Paradosso della ruota,
Il
Paradosso dei quadrati:
i
quadrati sono solo una parte dei numeri naturali. E’ però possibile stabilire una
corrispondenza biunivoca tra N e l’insieme
dei quadrati, cioè una corrispondenza nella quale ad ogni numero naturale corrisponda uno
ed un solo quadrato
1
2
3
4
5
6
7
8
...
|
|
| |
|
| |
|
1
4
9
16 25 36 49 64 ...
I
quadrati sono perciò tanti quanti i numeri naturali e ciò significa che una parte può
essere “uguale” al tutto.
Il
Paradosso della ruota:
due
ruote concentriche, tali che la più grande rotoli sopra una retta, toccano con i loro
punti due segmenti di uguale lunghezza

facendo
fare un giro completo alla circonferenza più grande fino a D, la più piccola arriverà al punto B. Ma
CD = AB. “Or come dunque può
senza salti scorrere il cerchio minore una linea tanto maggiore della sua
circonferenza...”. Anche in questo caso ciò è dovuto alla possibilità di costruire
una corrispondenza biunivoca tra la circonferenza più grande e quella più piccola (e
quindi tra un segmento ed una sua parte propria): basterà infatti proiettare dal comune
centro i punti della circonferenza più piccola su queli della più grande. Il paradosso
sta dunque nella possibilità di stabilire una corrispondenza biunivoca tra un segmento
continuo e una sua parte propria.
Come
si è accennato sopra Galileo non riuscì a trovare una soluzione ai suoi paradossi e
questo fatto lo portò a negare, come matematico, la possibilità di indagare
l’infinito: quando “siamo tra gl’infiniti e gl’indivisibili, quelli
[gl’infiniti] sono incomprensibili dal nostro intelletto finito per la loro
grandezza, e questi [gl’indivisibili] per la loro piccolezza”; tuttavia Galileo,
come filosofo, si permise di fare delle congetture “arbitrarie e non necessarie”
sulla natura dell’infinito e questo è il suo più grande merito.
Gli
infinitesimi e il calcolo infinitesimale
Un
accenno, anche se breve, è opportuno fare allo sviluppo del calcolo infinitesimale (è
l’infinito, l’inesauribile, quindi l’infinitamente grande che qui prendiamo
in considerazione) soprattutto per ragioni di completezza.
I
primi veri e propri strumenti algoritmici per il calcolo con gli infiniti e con gli
infinitesimi comparvero nel Cinquecento. Tra i precursori ricordiamo Pier Antonio Cataldi
che, elaborò la teoria delle frazioni continue, che, esprimendo una somma di infiniti
addendi, sono il prototipo delle serie numeriche.
Da
ricordare ancora J. Keplero, che ricondusse il calcolo dell’area del cerchio alla
somma delle aree degli infiniti triangoli isosceli aventi il vertice nel centro del
cerchio e come base una corda infinitesima della circonferenza.
Ma
soprattutto sono da menzionare i discepoli di Galilei: Cavalieri, Torricelli, Bonaventura
ed altri che gettarono le basi del calcolo infinitesimale che venne sviluppato e
sistematizzato da Newton e Leibniz.
Questi
primi tentativi furono accompagnati da polemiche e discussioni molto accese: si mettevano
in dubbio la legittimità del metodo degli indivisibili di Cavalieri, si criticava
l’uso spregiudicato delle quantità infinitesime. Il problema fondamentale era la
difficoltà a capire e spiegare come procedimenti fondati su basi così insicure e spesso
anche contraddittorie, portassero a molti utili risultati soprattutto nella meccanica, nella astronomia e nelle scienze sperimentali in
genere.
Solo
nell’Ottocento, grazie all’opera di Chauchy e di Weierstrass, si assistette ad
una revisione critica dei fondamenti dell’analisi infinitesimale, la quale venne
sistematizzata, raggiungendo un perfetto rigore logico, mediante l’introduzione del
concetto di Limite, che permise di eliminare definitivamente l’infinito e
l’infinitesimo attuali da tale teoria.
Le
sezioni di Dedekind
R.
Dedekind nel 1872 affrontò e risolse come due aspetti di uno stesso problema le due
grandi questioni che avevano messo in crisi l’infinito potenziale aristotelico: i
numeri irrazionali e il “continuo”.
Egli
si chiese che cosa caratterizzasse il continuo rispetto ai razionali.
Galilei
e Leibniz avevano affermato che la “continuità” dei punti di una retta fosse
dovuta alla loro densità, cioè al fatto che tra due punti qualsiasi esiste sempre un
terzo punto.
Tuttavia
anche i numeri razionali godono di questa proprietà, ma non formano un continuo; non è
possibile cioè costruire una corrispondenza biunivoca tra i punti di una retta e i numeri
razionali: infatti si fissi sulla retta r un
punto O ed una unità di misura u e si faccia corrispondere ad un numero razionale
a il punto P della retta la cui distanza da O sia individuata dal segmento di lunghezza a.
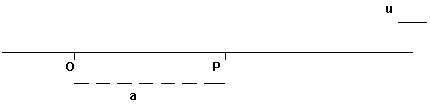
Si crea così una corrispondenza tra i punti della
retta ed i numeri razionali; tale corrispondenza, però, non è biunivoca
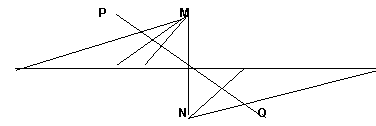
perché ad infiniti punti della retta non corrisponde alcun numero
razionale come nel caso del punto Q del seguente disegno la cui distanza
da O è pari alla lunghezza della diagonale
del quadrato di lato 1,
che come è noto, è radice quadrata di 2
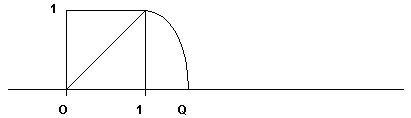
Per
risolvere i due aspetti di questo problema, cioè dare una definizione di continuità e
“scoprire” i numeri “mancanti” per creare una corrispondenza biunivoca
con la retta, Dedekind procedette nel seguente modo:
1. fissò
assiomaticamente una proprietà che caratterizzasse la continuità della retta;
2. definì
i numeri “reali” in modo da poter costruire una biiezione tra una retta e tali
numeri.
Relativamente
al primo problema Dedekind stabilì che l’essenza della continuità non sta tanto
nella densità dei suoi punti, quanto in una proprietà esattamente contraria, cioè nella
particolare natura della divisione di un segmenti in due parti mediante un punto giacente
su di esso: in qualsiasi divisione di un segmento (o di una retta) in due classi tali che
ciascun punto appartenga ad una ed una sola classe e che
ogni punto della prima classe si trova a sinistra di ciascun punto dell’altra,
c’è uno ed un solo punto che determina la
divisione.
Il
secondo problema fu risolto osservando che ogni numero razionale x individua analogamente una “sezione”
del corpo razionale, individua cioè una coppia di classi A1 , A2 tali
che ogni numero di A1 è minore di
ciascun numero di A2, mentre x è il più grande numero di A1 o il più piccolo di A2; esso risulta comunque univocamente determinato dalla coppia (A1, A2) per cui si può dire che x sia
la coppia (A1, A2).
Ma
non sempre una coppia (A1, A2) che sia una sezione dei razionali
può individuare un numero razionale, così come ad una sezione (cioè ad un punto) della
retta non sempre corrisponde un razionale (è il caso del punto Q dell’esempio precedente); ogni volta che
ciò accade, allora, è legittimo, pensò Dedekind, “creare” un nuovo numero y che corrisponda alla coppia (A1, A2), cioè che sia esso stesso la
coppia (A1, A2). Tale numero è un irrazionale.
La
proprietà di continuità del corpo reale (razionali e irrazionali), risulta così
collegata alla continuità della retta e tuttavia la definizione di numero reale, e in
particolare di numero irrazionale, è del tutto “sganciata” da una eventuale rappresentazione geometrica; è
proprio questo che conferisce agli irrazionali “dignità” di numero: il fatto
che la loro esistenza prescinda da una qualsiasi visualizzazione geomerica.
“Tuttavia
l’irrazionale non è un infinito attuale in senso categorico, esso è piuttosto
l’invisibile soluzione di un processo illimitato e teleologicamente ordinato. E’
perciò opportuno vedere nella ‘sezione’ di Dedekind non tanto un
‘taglio’ che indichi una effettiva locazione del numero, quanto piuttosto una
approssimazione successiva a due limiti tra loro adiacenti della classe inferiore A1 e della classe superiore A2 ed
è perlomeno discutibile, in linea di principio, configurarsi il limite di tale processo
come un’entità realmente osservabile, quale potrebbe apparire un punto geometrico: il numero irrazionale è lo stesso processo”
(P.Zellini).
Cantor
e i paradossi dell’infinito attuale
“Chiamiamo equivalenti
due insiemi M ed N, se è possibile porli in una relazione
tale che ad ogni elemento di uno di essi corrisponda un elemento e
uno soltanto dell’altro”.
Questa
definizione di equivalenza, o, come si dice oggi, di equipotenza, è nella sua semplicità ed
apparente banalità, una grande scoperta infatti
grazie a questa definizione,
estesa
da Cantor anche agli insiemi infiniti, fu possibile risolvere i paradossi che avevano
fermato Galilei.
Primo
Paradosso: una parte può essere uguale al tutto
purché non vi siano ambiguità nel significato che si dà alla parola ‘uguale’:
se per uguale infatti si intende identico (per colore, per forma,...) allora certamente
una parte non potrà mai essere uguale al tutto, perché il tutto contiene necessariamente
qualche elemento che nella parte, proprio perchè parte, non sta. Ma se per uguale si
intende equipotente nel senso della definizione di Cantor sopra riportata, cioè uguale per numero, allora questo è possibile. E’
possibile perciò che una parte sia uguale per numero al tutto, ma solo nel caso che gli insiemi siano infiniti:
questa è infatti una caratteristica degli
insiemi infiniti.
“Definizione:
Un sistema S si chiama infinito se è equipotente ad una sua parte
propria; nel caso opposto si chiama finito”.
Questa definizione apparsa nel quinto paragrafo del libro Il finito e l’infinito di Dedekind,
capovolge un modo di pensare millenario: si era sempre definito l’infinito a partire
dal finito, come non-finito; ora invece è il finito ad essere non-infinito.
Secondo
Paradosso: i punti dello spazio sono tanti quanti
quelli di un segmento piccolo a piacere.
Dimostramo
questa affermazione in tre momenti:
1.
Un quadrato di lato unitario ha tanti punti quanti un suo lato.Si
tratta di costruire una corrispondenza biunivoca tra i punti del quadrato e i punti di un
suo lato.Su un sistema di riferimento cartesiano sia Q un quadrato di vertici (0,0); (0,1); (1,1),
(1,0)
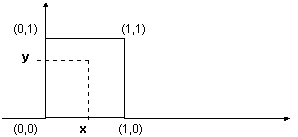
un
punto P del quadrato avrà coordinate (x, y)
dove x e
y sono misure di segmenti non maggiori del lato; essi sono perciò numeri compresi tra
0 e 1
e possono essere scritti in forma decimale:
x
= 0,a1a2a3...
y = 0,b1b2b3...
dove ai
e bi sono cifre comprese tra 0 e 9
(ad esempio 0,97563...); ci sono allora due possibilità:
· x
e y sono numeri razionali (cioè numeri decimali con
parte decimale finita o periodica)
· x
e y sono numeri irrazionali (cioè numeri
decimali con parte decimale infinita, aperiodica).
Alla
coppia ordinata (x, y), che identifica
univocamente il punto P, si può far
corrispondre il numero reale compreso tra 0 e 1
t = 0,a1b1a2b2a3b3...
che
identifica univocamente un punto del lato del quadrato.Viceversa ad un qualunque punto del
lato cui corrisponde univocamente il numero
t
= 0,t1t2t3t4t5t6...
si
può far corrispondere la coppia ordinata
x = 0,t1t3t5... y
= 0,t2t4t6...
che
individua un punto del quadrato.
La corrispondenza biunivoca tra punti del quadrato e punti di un suo lato è così
costruita e l’affermazione iniziale è perciò dimostrata.
2.
Un cubo di lato unitario ha tanti punti quanti un suo lato.
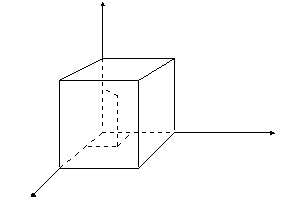
Analogamente
a quanto visto sopra ad un punto P del cubo
corrisponde una terna di punti (x, y, z)
con x, y
e z compresi tra 0 e1.
Siano perciò
x =
0,a1a2a3...
y
= 0,b1b2b3...
z = 0,c1c2c3...
si
può allora far corrispondere ad essi il punto
t = 0,a1b1c1a2b2c2a3b3c3...
anche
esso compreso tra 0 e1. Viceversa
al punto
t = 0,t1t2t3t4t5t6...
si
può far corrispondere il punto del cubo di coordinate
x
= 0,t1t4...
y = 0,t2t5...
z
= 0,t3t6...
ed
anche in questo caso si è costruita una corrispondenza biunivoca tra tutto il cubo ed un
suo lato.
3.
Lo spazio ha tanti punti quanti un segmento piccolo a piacere.
Basterà
pensare di ingrandire il cubo fino a fargli invadere tutto lo spazio. D’altra parte
il suo lato, che “è diventato” una retta, contiene tanti punti quanti un
segmento piccolo a piacere come fa vedere, meglio di una lunga spiegazione, la figura:
Conseguenza
sorprendente di queste affermazioni è che la
dimensionalità non costituisce un criterio per stabilire la potenza di un insieme
(infatti segmento, quadrato, cubo, spazio sono tutti equipotenti).
I
numeri transfiniti
“Dopo
Kant ha acquistato cittadinanza tra i filisofi la falsa idea che il limite ideale del
finito sia l’assoluto, mentre in verità tale limite può venir pensato solo come transfinito [...] e precisamente come il minimo di tutti i transfiniti...” (G.
Cantor 1885).
L’idea
dominante fino a Cantor era stata infatti che se l’infinito esiste allora è unico,
è l’assoluto oltre il quale non si può andare. Cantor dimostrò invece che esistono
infiniti più grandi e infiniti più piccoli.
Si
chiami numerabile ogni insieme che possa essere messo in corrispondenza biunivoca con
l’insieme dei numeri naturali N, cioè
equipotente ad N, e potenza del numerabile o X
0 tale
numero cardinale infinito.
Cantor
dimostrò con estrema semplicità due fatti apparentemente straordinari e cioè che i
numeri interi (...-3, -2, -1, 0, 1, 2, 3, ...) e
i numeri razionali sono insiemi numerabili.
1.
I numeri interi sono un insieme numerabile.
L’affermazione
sarà provata se si riuscirà a costruire una corrispondenza biunivoca tra N e Z
(= insieme degli interi).
Per
fare ciò basterà ordinare gli elementi di Z
in modo opportuno (non necessariamente corrispondente a quello naturale):
0
1 -1 2 -2 3 -3 ...
la
corrispondenza biunivoca con N è presto fatta:
0
1
2
3
4
5
6 ...
| |
|
|
| |
|
0
1 -1 2 -2 3 -3 ...
2.
I
numeri razionali sono un insieme numerabile.
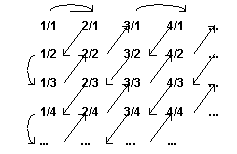
Anche
in questo caso basterà ordinare i razionali in modo “adeguato”, tenendo conto
tra l’altro che non esiste un ordinamento naturale, cioè secondo grandezza, per le
frazioni visto che tra due razionali se ne può sempre trovare un altro. Converrà
ordinare quindi le frazioni nel senso della freccia:
Si
potrà ora costruire una corrispondenza biunivoca tra Q (l’insieme dei razionali) ed N nel modo seguente:
1 2 3 4 5 ...
| |
|
|
|
1/1 2/1 1/2 1/3 2/2 ...
Gia
da questi esempi si può vedere come molti insiemi che sembrano più grandi dei numeri
naturali sono in realtà numerabili, ma non ogni
insieme infinito è numerabile.
Dimostrando
quest’ultima affermazione il 12 Dicembre 1873 Cantor fece fare un passo avanti al
pensiero matematico e filosofico e provò l’esistenza dell’infinito attuale
transfinito, sempre accrescibile, non assoluto.
Infatti
l’insieme dei punti di un segmento non è numerabile:
si
supponga per assurdo che i numeri reali compresi tra 0 e 1 (cioè
il segmento di estremi 0 e 1) siano numerabili; essi potranno allora essere
espressi come numeri decimali e potranno essere ordinati secondo l’ordine numerabile:
a1 = 0,a11a12a13...
a2 = 0,a21a22a23...
...
ma
allora il numero
b = 0,b1b2b3...
tale
che
bk = 9 se
akk =1
e
bk = 1 se akk
>< 1
è
diverso da tutti quelli elencati ed è compreso tra 0 e 1,
contro l’ipotesi di aver elencato tutti i numeri reali tra 0 e 1.
Conseguenza
di ciò è che i punti di un segmento sono più dei naturali, cioè più di X0
.
essi saranno X1
(con X0
< X1)
ed X1
si chiamerà potenza del continuo.
“Questa
dimostrazione appare degna di nota non solo a causa della sua grande semplicità, ma,
specificatamente, anche perché il principio in essa seguito si lascia senz’altro
estendere al Teorema generale, che le potenze di insiemi ben definiti non abbia alcun
massimo, ossia, il che è lo stesso, che ad ogni insieme dato L può essere messo a fianco un altro indieme M di potenza maggiore di L” (G. Cantor).
Prima
di affrontare la dimostrazione del Teorema generale di cui parla Cantor, è opportuno
ricordare il seguente teorema:
dato
un insieme A di n elementi, tale cioè che
| A | = n
l’insieme
delle sue parti, ossia l’insieme i cui elementi sono i sottinsiemi di A, in simboli P(A), avrà 2n elementi, cioè
|P(A)|
= 2n
n
Conseguenza
di ciò è che l’insieme delle parti di P(A)
avrà allora 22 elementi e così via.
E’
questo dunque il metodo per costruire insiemi di potenza via via crescente
all’infinito: partendo dai numeri naturali avremo:
X0
|N| = X0
|P(N)| = 2X0
|P(PN))| = 22 ...
Cantor
riuscì così a dimostrare l’esistenza di
infiniti numeri transfiniti maggiori di X0.
Egli
dimostrò inoltre che 2X0
=
X1,
cioè che la potenza del continuo ha la stessa
cardinalità dell’insieme delle parti di N.
Cantor
ipotizzò, ma non riuscì a dimostrarlo, che il continuo è la potenza immediatamente successiva al
numerabile (ipotesi del continuo).
Le
Antinomie
La
Teoria di Cantor fece esplodere nuove, clamorose antinomie. Se ne prendono qui in
considerazione due: l’antinomia di Russel e l’antinomia di Cantor.
1.
Antinomia di Russel:
Alcuni
insiemi sono elementi di se stessi, altri non lo sono: l’insieme di tutti gli insiemi
con più di 10 elementi è elemento di se stesso, mentre l’insieme di tutti i libri
non è elemento di se stesso (non è un libro).
Consideriamo
ora l’insieme di tutti gli insiemi che non sono elementi di se stessi. Se esso è un
elemento di se stesso, allora non è un elemento di se stesso. Se non lo è, lo è.
Questa
antinomia venne accolta con costernazione dal Frege in quanto dimostrava erronea l’
“ipotesi fondamentale” su cui egli intendeva costruire l’aritmetica ( i
suoi “Fondamenti dell’aritmetica” basati su tale ipotesi erano già in
bozze quando Russel gli comunicò la sua scoperta). Tale “ipotesi fondamentale”
può essere così formulata: ogni proprietà
definisce l’insieme degli elementi che la verificano (cioè la sua estensione).
L’Antinomia
si riferisce all’uso della parola “tutti” come possibilità di costruire,
in generale, l’insieme “estensione” di una proprietà.
2.
Antionmia di Cantor o della classe totale:
Si
consideri la totalità degli insiemi, la “classe totale” A, che potremo chiamare l’insieme di tutti
gli insiemi. Sia allora P(A) l’insieme
delle parti di A. Per quanto precedentemente
visto P(A) dovrebbe avere potenza maggiore di A, ma essendo A l’insieme di tutti gli insiemi, esso
contiene P(A) come suo elemento, quindi P(A) dovrebbe avere cardinalità non maggiore di A.
Queste
Antinomie determinarono una crisi dei fondamenti
della Matematica che scosse il mondo matematico al’’inizio del secolo e
determinò la nascita di diverse concezioni circa la natura della Matematica:
· gli Intuizionisti (uno dei maggiori esponenti di
questa corrente di pensiero fu Brower) accettarono come vero esclusivamente il Postulato ristretto della Matematica, cioè
l’esistenza della successione infinita dei numeri naturali e tutto ciò che da essa
conseguiva; rifiutarono il Principio del terzo escluso affermando che una proposizione
può essere ne’ vera ne’ falsa, cioè indecidibile e, conseguentemente, negarono
valore alle dimostrazioni per assurdo: affermare perciò che esiste un oggetto dotato di
certe proprietà significa che c’è un metodo riconosciuto che permette di trovare o
di costruire tale oggetto mediante un numero finito di passi
· i
Formalisti (il fondatore di questa scuola di
pensiero fu Hilbert) partirono dall’idea che esistenza
in Matematica significa coerenza, cioè non contraddizione e poiché la coerenza delle
teorie più complesse si riconduceva alla coerenza dell’aritmetica, concentrarono i
loro sforzi nel tentativo di formalizzare completamente l’aritmetica. Alcuni
svilupparono tale posizione fino alle estreme conseguenze, giungendo alla conclusione che
la Matematica non è altro che un gioco privo di significato in cui si gioca
concontrassegni privi di significato secondo delle regole formali concordate in partenza
· i
Logicisti (un esponente di rilievo fu Russel) che tentarono di formalizzare la Matematica
con la Logica: essi affermavano che i numeri interi sono sufficienti a descrivere i
risultati dell’Analisi, ma essi sono stati a loro volta descritti nella Ligica
Simbolica di Peano la quale forniva, a loro giudizio, un tessuto logico primario che
sembrava avvalorare dall’esterno (al di fuori della Matematica) la Matematica stessa.
Nel
1931 Godel dimostrò tuttavia che la Matematica mostrava comunque delle
“aperture”, delle allusioni ad “altro” rispetto a ciò che essa
sarebbe in ogni caso riuscita ad esprimere, infrangendo così i sogni dei formalisti che
speravano di costruire un mondo chiuso ed esauriente di segni, un sistema formale
completo; in altre parole Godel provò che all’interno del sistema esistono certe
asserzioni ben precise che non possono essere ne’ dimostrate, ne’ invalidate
nell’ambito degli assiomi del sistema; perciò, usando i metodi convenzionali, non si
può essere certi che gli assiomi dell’aritmetica non portino a contraddizioni.
Nel
1964 Paul Cohen costruì un sistema formale che verifica tutti gli assiomi
“ordinari” e nel quale però l’Assioma del Continuo di Cantor è rifiutata,
dimostrando così che è possibile costruire tanto una “Matematica cantoriana”
quanto una “Matematica non cantoriana” analogamente a quanto era avvenuto in
Geometria un secolo prima con la nascita delle Geometrie non euclidee (che rifiutavano tra
i loro assiomi il V Postulato di Euclide).
Nasce
così il Metodo Assiomatico moderno che non è soltanto deduttivo (si assumono come
verità primitive evidenti alcune proprietà fondamentali, chiamate “postulati”
o “assiomi”, dalle quali si deducono nuove proprietà), ma è
ipotetico-deduttivo: gli assiomi non sono più verità primitive indimostrabili, ma
semplici ipotesi relative ad enti del pensiero non definiti perciò, se si considerano
enti concreti che verificano le proprietà espresse dagli assiomi, allora valgono anche le
proprietà espresse dai teoremi dedotti da questi per via strettamente logica. Ad ogni
interpretazione degli enti primitivi corrisponde un modello (concreto) della teoria
assiomatica (di per se’ astratta, formale).
Se
l’assunzione del metodo assiomatico moderno comporta la perdita dell’unità: non
esiste più la Matematica, ma esistono le Matematiche (come non c’è più la
Geometria, ma le Geometrie), apre d’altro canto nuovi vastissimi campi di ricerca e
quindi nuove prospettive di progresso sia del pensiero matematico che, conseguentemente,
del pensiero scientifico e ed pensiero umano in generale.
a
cura di: Maria Chiara Giacomucci
Bibliografia
L.
Lombardo Radice “L’infinito” Ed Riuniti
P. Zellini “Breve
storia dell’infinito”
Ed. Adelphi
B. Russel “Introduzione
alla filosofia matematica”
C. B. Boyer “Storia
della matematica” Ed.
Mondadori |