PROGETTO DI UN SERBATOIO PER ACQUA IN LEGNO

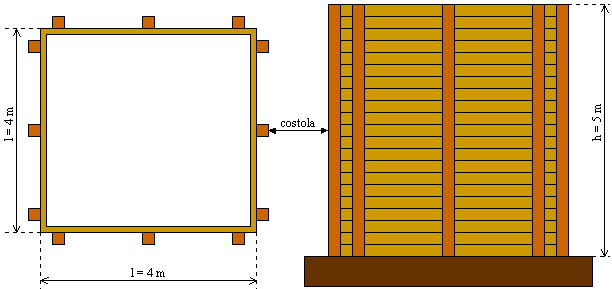
Si deve costruire un serbatoio per acqua in legno, le dimensioni del quale appaiono in figura. Eseguire il calcolo di massima delle sezioni resistenti.



PREMESSA

La pressione esercitata da un liquido è una grandezza scalare, cioè ha lo stesso valore in qualunque direzione: in un dato punto con un certo affondamento la pressione verso l'alto o il basso o a destra o a sinistra è la stessa, perché la pressione non è un vettore.
E' invece un vettore, anzi una forza(*), l'azione della pressione su una superficie, come si ricava subito dalla definizione:
p = F / A                dalla quale si ricava                F = p A
che possiamo tradurre in questo modo: il prodotto fra la pressione e l'area della superficie sulla quale essa agisce è una forza, solitamente chiamata spinta.
E' possibile "vedere" questa forza? E' abbastanza facile: se prendiamo un recipiente pieno di acqua e facciamo un foro nella parete vedremo l'acqua uscire con una certa forza. Man mano che il livello d'acqua diminuisce, diminuisce anche la distanza raggiunta dal getto di liquido, indicando che la forza che lo spinge diventa più piccola.
La legge fondamentale della dinamica assicura che affinché una massa si muova occorre l'azione di una forza: il liquido che si trovava dove ora c'è il foro era fermo; se ora esso si muove significa che è soggetto all'azione di una forza, detta spinta; e il fatto che la forza decresca al diminuire del livello del liquido indica che tale forza dipende dalla pressione.
Quanto vale la pressione? Oggi è facile misurarla con un manometro e, ruotando lo strumento, è facile verificare che ha lo stesso valore in tutte le direzioni. Vediamo di trovare una espressione matematica per esprimerla. Consideriamo un quadrato di lato un millimetro(**) sul fondo orizzontale del recipiente: sia g il peso specifico del liquido e h l'affondamento, cioè la quota sotto il pelo libero. Sulla superficie del quadrato grava il peso P della colonna di liquido alta h che lo sovrasta, peso che vale il peso specifico g per il volume del parallelepipedo con base A di un millimetro quadrato e altezza h, cioè:
P = g V = g A h            dalla quale si ricava la pressione           p = P / A = g A h / A = g h
Siccome la pressione è indipendente dalla direzione, se vale g h su una superficie orizzontale, vale altrettanto su una uguale superficie verticale. Se consideriamo una striscia orizzontale in tutti i punti c'è la stessa pressione. Se invece la striscia è verticale (o inclinata) si deve tener conto che i suoi punti si trovano a quote di affondamento diverse e quindi la pressione è diversa di quota in quota.
Ciò si ricava direttamente dalla legge p = g h dalla quale si vede che p varia proporzionalmente ad h: cresce h cresce p, diminuisce h diminuisce p. Il diagramma della distribuzione della pressione su un segmento verticale è quindi un triangolo.
Per trovare la spinta(***) basta moltiplicare la pressione per l'area della superficie della striscia in esame. Se la striscia è orizzontale non ci sono problemi. Se invece è verticale bisogna prendere la pressione media agente sulla striscia e moltiplicare per la sua area.

SVOLGIMENTO

A) AZIONE SULLE STRISCE ORIZZONTALI

Prendiamo in esame una striscia alta d = 1 mm = 0,001 m della tavola aderente al fondo, cioè della tavola soggetta alla massima pressione. La spinta su di essa vale:
S = g h A = g h d l = 1.000 x 5 x 0,001 x 4 = 20 kg
Questa forza agisce complessivamente sulla striscia alta 1 mm. Dividendo S per la lunghezza della striscia troviamo il carico su un metro di lunghezza, cioè troviamo il carico distribuito uniformemente sull'asse della striscia:
q = S / l = 20 / 4 = 5 kg / m
Ora ribaltiamo di 90 gradi la striscia riducendola al suo asse, rappresentiamo il carico q come se fosse verticale, e la consideriamo come semplicemente appoggiata alle costole (vedi figura).



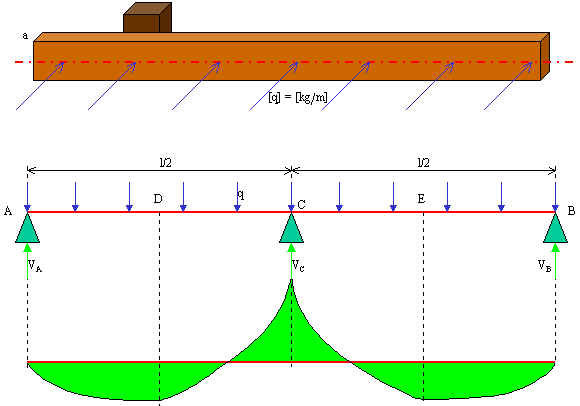
Nella figura centrale sono rappresentate le reazioni sugli appoggi e nella figura più in basso è rappresentato il diagramma del momento flettente (senza scala). I valori numerici sono i seguenti (le formule vengono dal Manuale Colombo):
V_A = V_B = 12 q l / 64 = 12 x 5 x 4 / 64 = 3,75 kg                V_C = 5 q l / 8 = 5 x 5 x 4 / 8 = 12,50 kg
M_C = - q l² / 32 = - 5 x 4² / 32 = - 2,5 kg m = - 2.500 kg mm
M_D = M_E = 18 q l² / 1.024 = 18 x 5 x 4 / 1.024 = 1,41 kg m = 1.410 kg mm
Usando legno duro da costruzione si ha:
nella zona tesa s_amm = 1 kg / mm²                nella zona compressa s_amm = - 0,6 kg / mm²
In C si ha il valore assoluto massimo e il calcolo si deve svolgere dalla parte compressa della sezione.
Detto a lo spessore delle tavole, la sezione resistente a flessione è A = a d. Gli elementi geometrici per il progetto sono ancora J = d a³ / 12, y = a / 2 e quindi
s_C = M_C y_C / J_C = M_C a / 2 d a³ / 12 = 6 M_C / d a² = s_amm = - 0,6 kg / mm²
dalla quale si ricava          a_C = (6 M_C / s_amm)^1/2 = (6 x 2.500 / 0,6)^1/2 = 158 mm arrotondato 16 cm
s_D = s_E = M_D y_D / J_D = 6 M_D / d a² = s_amm = - 0,6 kg / mm²
dalla quale si ricava          a_D = a_E = (6 M_D / s_amm)^1/2 = (6 x 1.410 / 0,6)^1/2 = 119 mm arrotondato 12 cm
Questi risultati dicono che: le tavole devono avere uno spessore di 12 cm (sezioni D - E); tavole più costole devono avere uno spessore di 16 cm (sezione C); la costola deve avere uno spessore di 16 - 12 = 4 cm.

b) AZIONE SULLE STRISCE VERTICALI

Sviluppiamo il progetto di massima, come se l'unica possibile azione fosse quella di flessione che tende a rovesciare le pareti del serbatoio verso l'esterno (azione di ribaltamento o rovesciamento).
Prendiamo in esame una striscia verticale larga b = 0,001 m e di altezza h. La spinta S (vedi figura) ha un braccio pari ad h / 3 e quindi sviluppa un momento flettente M = S h / 3 rispetto alla base del serbatoio. Possiamo quindi calcolare quale sezione devono avere le tavole per sopportare tale momento(****). La spinta è un carico distribuito con legge triangolare con risultante S = g h² b / 2 = 1.000 x 5² x 0,001 / 2 = 12,5 kg. Il valore del carico va da g h = 1.000 x 5 x 0,001 = 5 kg / m al piede sino a 0 nel pelo libero.




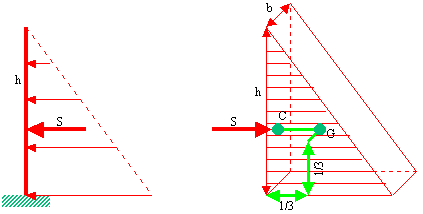
Tenendo conto di quanto si è detto abbiamo:
M = S h / 3 = 12,5 x 5 / 3 = 4,18 kg m = 4.180 kg mm
a '_C = (6 M / s_amm)^1/2 = (6 x 4.180 / 0,6)^1/2 = 204 mm arrotondato 21 cm
Poiché a '_C > a_C bisogna adottare questa soluzione.

COMMENTO

A) Non si è tenuto conto del vincolo negli spigoli: le tavole saranno inchiodate fra loro utilizzando un profilato angolare ad L di metallo.
B) Non si è tenuto conto che le strisce cooperano(******) fra loro, nel senso che NON si può fare il calcolo facendo finta di poter estendere a tutta la parete ciò che accade ad una sua porzione.
C) L'azione di rovesciamento è PROBABILMENTE la più pericolosa: ho detto probabilmente perché se non si fanno i calcoli relativi alla parete intera non si può affermare niente di sicuro.
D) Le costole d'angolo sono male utilizzate: si trovano infatti dove il momento flettente è nullo o quasi.
E) Ovviamente le tavole possono avere minore spessore man mano che si sale verso il pelo libero.
F) Tenendo conto di A) e D) è più utile disporre le costole ad una certa distanza dagli spigoli in modo da realizzare uno schema statico simile a quello della figura seguente:



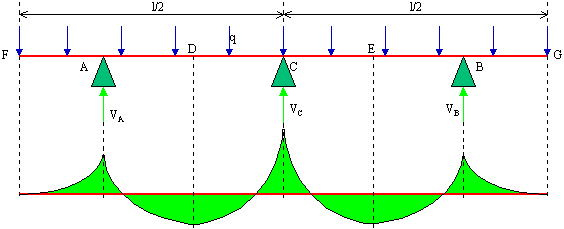
In questa situazione infatti i momenti flettenti hanno sicuramente valori minori di quello M_C calcolato in precedenza(*****).


(*) Qui occorre fare molta attenzione: la forza è una grandezza di tipo vettoriale (può infatti essere rappresentata per comodità con un vettore) ma non è un vettore. I vettori infatti sono descritti compiutamente assegnando tre parametri: modulo, direzione e verso. Per descrivere una forza occorrono invece quattro parametri: modulo, direzione, verso e punto di applicazione. Dire che la forza è un vettore è come dire che un triangolo è uguale a un quadrato. Queste due figure hanno delle cose in comune: sono composte di angoli e lati e chiudono una superficie, ecc. ma di certo non sono uguali. La pressione è ancora più povera del vettore: per descriverla basta un solo parametro, cioè il modulo!
(**) Aver scelto un millimetro quadrato dipende solo dall'aver voluto considerare una superficie che "assomiglia" ad un punto e metterlo orizzontale o verticale non cambia nulla.
(***) La spinta è una forza e quindi bisogna definire i quattro parametri che la descrivono: 1) la spinta è perpendicolare alla superficie (se questa è orizzontale la spinta è verticale e viceversa); 2) la spinta è sempre diretta contro la superficie; 3) la spinta vale S = g h A; 4) la spinta ha il punto di applicazione C nella proiezione ortogonale sulla superficie, del baricentro G del diagramma delle pressioni, come indicato nella figura qui sotto:



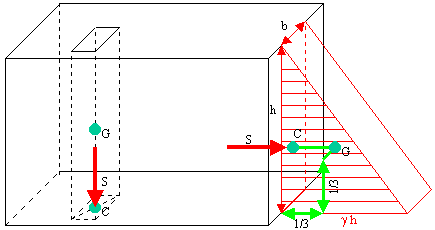
Ricordiamo che il baricentro di un triangolo rettangolo è all'incrocio dei terzi inferiori dei cateti. Poiché il diagramma è un prisma bisogna poi andare alla mezzeria dello spessore.
Dette b e h le dimensioni della striscia verticale della figura, la spinta totale su di essa vale:
S = g h_m A = g h A / 2 = g h b h / 2 = g h² b / 2
Questa espressione è proprio il volume del prisma triangolare di base A = b h e di altezza p = g h.
Il punto di applicazione (detto CENTRO DI SPINTA) è il punto C che è la proiezione ortogonale del baricentro G del volume di pressione.
Quando la superficie è inclinata si calcola la spinta sulla proiezione orizzontale e verticale e poi se ne fa la somma.
(****) L'ipotesi in questa situazione è che la striscia sia incastrata al piede.
(*****) Con questo schema statico si è implicitamente supposto che in F e in G ci siano due cerniere (collegamento con la parete adiacente).
(******) La parete, se ben costruita, si comporta come una piastra e le relazioni che ne permettono il calcolo sono ben diverse da quelle che si adoperano per il calcolo delle travi.


PROBLEMA CHE LASCIO AI MIEI LETTORI: SE LO SCHEMA STATICO DIVENTA QUELLO DELLA FIGURA SEGUENTE, COSA E COME CAMBIA?




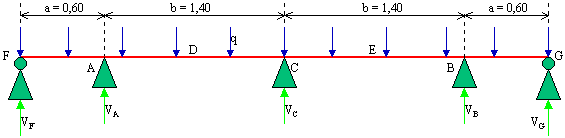
NOTA NENE: questa trave come la precedente è iperstatica e quindi le formule risolutive vanno cercate in un apposito manuale, se non si sanno trovare direttamente.
SCRIVETEMI!