f006 Tagliare una torta
 |
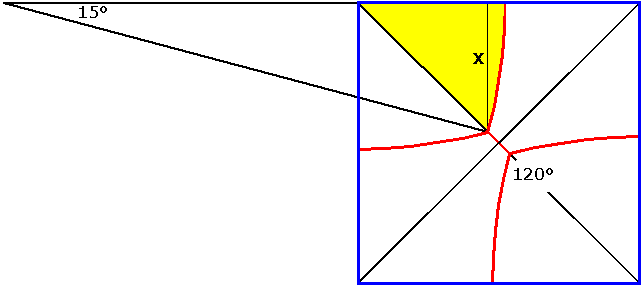| La soluzione trovata: I tagli (linee rosse) hanno una lunghezza complessiva di 1.975592884 La costruzione : Individuare gli archi, di ampiezza 15°, che formano tra loro un angolo di 120°, in modo che l'area compresa tra arco, diagonale e lato (area gialla) sia pari a 1/8. x = sqrt(3/(pi-3sqrt(3)+3))*(sqrt(6)-sqrt(2))/4 |
Segue l'intera discussione come apparsa nel NG
Da: "Crios"
<Crios@cclinf.polito.it>
Data: giovedì 6 luglio 2000 12.24
Trovare un insieme di tagli di lunghezza complessivamente
*minima*, tale da dividere una torta quadrata di lato unitario in
4 pezzi di area identica.
Naturalmente, a chi indovina gli regalo la torta...
Da: "El Filibustero"
<spalland@comune.re.it>
Data: giovedì 6 luglio 2000 17.32
Ciao Crios, per iniziare: fare due fette A e B a forma di
quadrato con un angolo arrotondato e tagliare l'istmo lungo la
diagonale.
+--------------------+ | | | | | | | A | | | / _________| |________/\/ | | / | | | B | | | | | | | +--------------------+
La scelta ottimale del lato di A e B e del raggio dello smusso da' un lato di 0.5007645975 e un raggio di 0.05971256335 per un taglio di lunghezza complessiva di 1.999105585. Ciao
Da: "Marco Beleggia"
<beleggia@df.unibo.it>
Data: giovedì 6 luglio 2000 12.38
Io proporrei due tagli a iperbole, congiunti da un pezzo di
diagonale.
Non riesco a fare disegni, comunque si riesce a stare sotto la
lunghezza due, per diversi parametri. Per ora ad esempio potrei
offrire un taglio di lunghezza 1.99808, inferiore a quello
proposto da El Filibustero.
Spiegare per bene le cose e' quasi piu' arduo che fare i calcoli.
Appena trovo un minimo assoluto lo scrivo con la procedura
completa. Cmq e' stata una faticaccia.
Ciao
Marco
Da: "Silvio Sergio"
<mg9322@mclink.it>
Data: giovedì 6 luglio 2000 13.57
Ma siete sicuri che a far tagli curvi ci si guadagni?
_________________ | ' | | | | | |. *A | | .| | B* | | | | | |_________._______|
A e B sono disposti simmetricamente sulla diagonale e sono
congiunti ai lati da segmenti rettilinei.
Se non ho sbagliato i calcoli facendo A e B distanti 0.061047854
si ottiene un taglio lungo 1.98108902
Ricontrollero`
Silv:o)
Da: "Marco Beleggia"
<beleggia@df.unibo.it>
Data: giovedì 6 luglio 2000 14.46
> Ma siete sicuri che a far tagli curvi
ci si guadagni?
No in effetti. Pensavo a una geodetica di qualche tipo, e allora
ho puntato con le curve.
Confermo il tuo risultato per la lunghezza del taglio, anche se
la distanza tra i punti da te chiamati A e B mi viene maggiore,
0.0863 circa.
Per distanza intendevi in realta' la proiezione sul lato? se e'
cosi' il mio risultato coincide col tuo.
Mi piacerebbe applicare un po' di calcolo variazionale al
problema, ma non sono in grado di affrontare la cosa.
Ciao
Marco
Da: "Silvio Sergio"
<mg9322@mclink.it>
Data: giovedì 6 luglio 2000 15.15
> Per distanza intendevi in realta' la
proiezione sul lato? se e' cosi' il mio risultato coincide col
tuo.
oooops, ho dimenticato il perRadiceDiDue.
> Mi piacerebbe applicare un po' di
calcolo variazionale al problema, ma non sono in grado di
affrontare la cosa.
...figurati io. Ne ho sentito parlare un gran bene, pero` :^)
Silv:o)
Da: "Crios"
<Crios@cclinf.polito.it>
Data: giovedì 6 luglio 2000 16.00
> Ma siete sicuri che a far tagli curvi
ci si guadagni?
Si, si guadagna.
Per non farvi fare calcoli micidiali vi avverto che il problema
cede ad alcune considerazioni...
... di statica dei fluidi.
Da: "Dario Uri"
<md4586@mclink.it>
Data: giovedì 6 luglio 2000 21.24
Silvio Sergio wrote:
> C________D________ > | ' | > | | > | | > |E *A | > | .| > | B* | > | | > | | > |_________._______|
Non ho controllato i tuoi conti, ma le esperienze di Steiner,
il punto di Fermat, e le lamine di sapone indicherebbero per il
minimo un incontro a 120 gradi dei tagli nei punti A e B.
In questo caso il triangolo CAD ha gli angoli di 45,60,75 gradi e
l'area di 0.125.
Risulta
AD=0.4597
CA = 0.627961..
AB = sqrt(2)-2*CA= 0.158291..
Totale tagli = 4*AD+AB = 1.99709..
:) dario
Da: "El Filibustero"
<spalland@comune.re.it>
Data: giovedì 6 luglio 2000 23.03
>> Ma siete sicuri che a far tagli
curvi ci si guadagni?
>Si, si guadagna.
Ciao Crios, per quella categoria topologica di tagli che abbiamo
proposto io, Marco Beleggia e Silvio Sergio, l'ottimo si ha
risolvendo il problema variazionale della minimizzazione di
sqrt(2)-f(0)+2[integrale{dt=0..pi/4} sqrt(f(t)^2+f'(t)^2]
con il vincolo
integrale{dt=0..pi/4} f(t)^2 = 1/4
dove la funzione incognita del taglio curvilineo f(t) e' il
raggio (in coordinate polari con polo in un vertice del quadrato)
in funzione dell'angolo t formato con la diagonale del quadrato.
Il minimo che ho trovato con una soluzione approssimata e' ~
1.9758
f(0) = 0.6523
f(pi/24) = 0.6088
f(2pi/24) = 0.5758
f(3pi/24) = 0.5515
f(4pi/24) = 0.5349
f(5pi/24) = 0.5252
f(6pi/24) = 0.5220
Ciao
Da: "Silvio Sergio"
<mg9322@mclink.it>
Data: giovedì 6 luglio 2000 0.58
> Ciao Crios, per quella categoria
topologica di tagli che abbiamo proposto io, Marco Beleggia e
Silvio Sergio, l'ottimo si ha risolvendo il problema variazionale
della minimizzazione di
>
> sqrt(2)-f(0)+2[integrale{dt=0..pi/4} sqrt(f(t)^2+f'(t)^2]
>
> con il vincolo
>
> integrale{dt=0..pi/4} f(t)^2 = 1/4
rettificazione e calcolo delle aree in coordinate polari ... può
addirittura essere che le abbia studiate, tempo fa :)
Ho provato a plottare la tua soluzione, e le curvature sono
appena accennate, mentre per t=0 c'e` un punto angoloso. In
definitiva, tra le approssimazioni proposte - quadrato smussato,
rami di iperbole, lati rettilinei non ortogonali - l'ultima
sembra la meno peggio.
... e stiamo dando per scontato che l'ottimo debba stare in
questa classe
(cos'altro, se no?).
Con che tecniche/software hai trovato la soluzione approssimata?
Ciao, Silv:o)
Da: "El Filibustero"
<spalland@comune.re.it>
Data: venerdì 7 luglio 2000 13.03
>Ho provato a plottare la tua soluzione,
e le curvature sono appena accennate, mentre per t=0 c'e` un
punto angoloso. In definitiva, tra le approssimazioni proposte -
quadrato smussato, rami di iperbole, lati rettilinei non
ortogonali - l'ultima sembra la meno peggio.
Pero' non sembra stabile. Procedendo per 48-esimi di pi si trova
0.6507 0.6276 0.6074 0.5896 0.5744 0.5615 0.5509
0.5423 0.5356 0.5306 0.5270 0.5246 0.5238
per una lunghezza di circa 1.9757; si nota che i valori di
posizione
pari sono notevolmente diversi dei corrispondenti dei 24-esimi di
pi:
0.6523 0.6089 0.5757 0.5514 0.5349 0.5253 0.5220
Frazionando ulteriormente l'angolo si trovano risultati peggiori.
>Con che tecniche/software hai trovato
la soluzione approssimata?
Matlab, funzione fmins (algoritmo del simplesso di Nelder-Mead).
Ciao
Da: "El Filibustero"
<spalland@comune.re.it>
Data: venerdì 7 luglio 2000 13.04
Ciao Crios, la soluzione si puo' esprimere come funzione
elementare?
Il taglio minimo e' di molto inferiore a 1.9757? Ciao
Da: "Crios"
<Crios@cclinf.polito.it>
Data: venerdì 7 luglio 2000 17.26
> Ciao Crios, la soluzione si puo'
esprimere come funzione elementare?
Si'.
> Il taglio minimo e' di molto inferiore
a 1.9757?
No. E' appena inferiore a questo valore.
Posso anche confermare che l'approccio e il valore dato da Dario
Uri
(per la sottoclasse di funzioni che ha preso in considerazione)
sono entrambi corretti.
Ciao.
Da: "El Filibustero"
<spalland@comune.re.it>
Data: venerdì 7 luglio 2000 17.13
>Per non farvi fare calcoli micidiali vi
avverto che il problema cede ad alcune considerazioni...
Probabilmente l'equazione differenziale di Eulero ha degli archi
di circonferenza come soluzione. Considero solo la classe di
archi che, partendo da un punto P della diagonale, incontrano
ortogonalmente il lato della torta (sembrano i piu' corti
rispetto agli altri). NB: P e' angoloso, in generale. Sia x la
distanza di P dal lato; la distanza di P dal centro del quadrato
risulta sqrt(2)(1/2-x). La condizione dell'area della fetta = 1/4
impone una relazione trascendente tra x e raggio r di curvatura
dell' arco:
r^2 arcsin(x/r) - x * sqrt(r^2-x^2) + x^2 = 1/4
la lunghezza complessiva del taglio e'
4 r arcsin(x/r) + sqrt(2)(1-2x).
Per tentativi ho trovato che per r=sqrt(3) e x=0.4600947472 la
lunghezza del taglio e' 1.975609257.
Ciao
Da: "Paolo Licheri"
<paolo.licheri@tin.it>
Data: sabato 8 luglio 2000 8.04
con un mix di tutte le considerazioni fatte nei messaggi
precedenti, ho trovato
1.975593 (salvo errori)con questo ragionamento :
l'arco cercato PV deve incidere a 90 gradi sul lato, e a 60 gradi
sulla
diagonale, (due archi si incontrano in P a 120 gradi)
U___________ A_____H_V________B . | | ' | . | | | . | | | . |. *P | . | .| . | Q* | . | | . | | . |_________._______|
allora, detta x la distanza di P dalla mediana (distanza
PH=1/2-x)
considerato un valore arbitrario di x, costruisco il triangolo
PHU, con angolo in U di 15 gradi, posso calcolare agevolmente, in
funzione di x, tuttu gli elementi del disegno, tra cui in
particolare, l'area del settore circolare UPV e del triangolo
UAP, e quindi la differenza, pari all'area APV
per tentativi cerco il valore di X per cui tale differenza vale
0.125
ho trovato:
x=0.0389587
arco PV=0.466350264
lunghezza totale di taglio=1.975592901
ciao
paolo
Da: "El Filibustero"
<spalland@comune.re.it>
Data: sabato 8 luglio 2000 11.24
>con un mix di tutte le considerazioni
fatte nei messaggi precedenti, ho >trovato 1.975593 (salvo
errori)con questo ragionamento :
>...
>allora, detta x la distanza di P dalla mediana (distanza
PH=1/2-x) >considerato un valore arbitrario di x, costruisco
il triangolo PHU, con >angolo in U di 15 gradi
OK! Partendo dal presupposto che l'arco abbia ampiezza angolare
di 15 gradi, non e' necessario andare per tentativi. La
condizione dell'area
(x ed r sono riferiti al mio post)
r^2 arcsin(x/r) - x * sqrt(r^2-x^2) + x^2 = 1/4
da' risultati non approssimati:
r = sqrt(3/(pi-3sqrt(3)+3))
x = r(sqrt(6)-sqrt(2))/4 =
sqrt(3/(pi-3sqrt(3)+3))*(sqrt(6)-sqrt(2))/4
che sostituiti nella formula della lunghezza danno il valore
esatto
sqrt(3)/3 sqrt(pi-3sqrt(3)+3) + sqrt(2) =~ 1.975592884
Quella di esprimere x ed r in funzione di alfa (ampiezza
dell'arco) anziche' viceversa (come avevo fatto io) e' un'ottima
idea che puo' condurre ad una dimostrazione formale, senza andare
per tentativi.
Infatti la lunghezza del taglio puo' venire espressa, tramite il
vincolo sull'area, come funzione di solo alfa:
lunghezza =
sqrt(2)*((alfa*sqrt(2)-sin(alfa))/sqrt(alfa-sin(2alfa)/2+sin(alfa)^2)+1)
La derivata rispetto ad alfa uguagliata a 0 da' un'equazione
trascendente, che pero' almeno si puo' verificare risolta da
alfa=pi/12. Cio' dimostra formalmente che
sqrt(3)/3 sqrt(pi-3sqrt(3)+3) + sqrt(2) =~ 1.975592884
e' il taglio minimo nella classe di tagli citata nel mio
precedente
post. Ciao
Da: "Silvio Sergio"
<mg9322@mclink.it>
Data: venerdì 7 luglio 2000 22.51
Ottimo lavoro. Un mix di raffinate tecniche matematiche (El
Filibustero), intuizione (Paolo), esperienza e conoscenza
(Dario).
Magari troveremo qualcosa di meglio, non lo so, aspettiamo anche
Crios e le sue considerazioni idrostatiche. Intanto mi pare siamo
arrivati ad un bel risultato.
Paolo, ovviamente lo inserisci nel sito!
Ciao, Silv:o)
Da: "Fernando
Cinquegrani" <f.cinquegrani@libero.it>
Data: sabato 8 luglio 2000 6.41
dio! ma questo è il thread dei geni.
ragazzi, riposatevi un attimo
dando un'occhiata al mio
'teorema' :-)))))) (booooh!)
http://digilander.iol.it/ProDomoSua/ppage05.html
(il secondo, ovviamente)
vi pregherei solo di
non demolirmelo:
sono anni che mi fa compagnia, e
sono già abbastanza sconvolto
per aver testè appreso dell'esistenza
di un punto angoloso!
Da: "Crios"
<Crios@cclinf.polito.it>
Data: giovedì 13 luglio 2000 13.20
> Magari troveremo qualcosa di meglio, non lo so, aspettiamo anche Crios e le sue considerazioni idrostatiche. Intanto mi pare siamo arrivati ad un bel risultato.
Eccomi.
Il problema e` equivalente a trovare i bordi di 4 bolle di sapone
chiuse in uno spazio quadrato. La tensione superficale e la
pressione interna agiscono in modo da minimizzare *localmente* la
superficie totale. In 2d la cosa si semplifica solamente. Le
forze di volume si trascurano Tutti i tagli devono essere archi
di circonferenza.
Dal diagramma di corpo libero di un elemento di superficie si
ottiene subito 2*t*c=p, con t la tensione `lineare`, c la
curvatura 1/R e p la differenza di pressione, costante
all`equilibrio. Da cui c costante.
In un punto di diramazione tutti gli angoli tra le tangenti sono
di 120 gradi.
Su di essi infatti agisce solo la tensione superficiale... se t_i
sono i versori...
t(t_1+t_2+t_3)=0...
Con piu` di 3 intersezioni il punto di diramazione e` instabile.
Analogo ragionamento per i punti ai bordi... la componente di
tensione lineare tangenziale...
Queste considerazioni non sono sufficienti in generale, neppure
per una soluzione localmente minima. Una breve riflessione
bastera` a comprenderlo. Ma per questo problema bastano.
Aggredendolo con tecniche puramente matematiche il problema e`
eccezionalmente difficile.
Io non riesco neppure a dimostrare che i tagli devono essere
archi di circonferenze, cosa apparentemente ovvia...
Riesco invece a dimostrare che in assenza di vincolo di area nei
punti di diramazione gli angoli sono di 120 gradi, ma anche qui
e` eccezionalmente arduo generalizzare.
Ciao, Crios.
Da: "Crios"
<Crios@cclinf.polito.it>
Data: giovedì 13 luglio 2000 14.01
> Queste considerazioni non sono
sufficienti in generale, neppure per una soluzione localmente
minima. Una breve riflessione bastera` a comprenderlo.
Esempio : torta triangolare, taglio con punto di diramazione
centrale a 120, taglio *curvo*, incidente ortogonalmente. Qui
occorre anche considerare la pressione. La cosa e` facile se si
trovano simmetrie.
> Ma per questo problema bastano.
Assi`, questa parte puo` essere debole...
Cosi` ho mostrato localmente l`ottimalita` nella classe di tagli
gia` presa in considerazione, nel senso che perturbandola di poco
si ottiene sempre un peggioramento.
Analizzando le alternative (sono circa 8, purtroppo non ho le mie
cartacce...), si dimostra abbastanza agevolmente che non vanno
bene.. tranne 2, segnatamente quelli in cui alla soluzione
'naturale', si sposta un taglio fino a fargli attraversare un
angolo.
Queste non le ho analizzate a fondo.
La mia sicurezza sta nel fatto che nel taglio ottimo il guadagno
e` sempre estremamente scarso, rispetto a uno con tagli
rettilinei.
RiCiao a tutti, il grande El Fili, Dario, Paolo, Silvio e
chiunque abbia seguito per diletto il problema, mi avete data
molta soddisfazione ;-),
Crios.
Da: "Paolo Licheri"
<paolo.licheri@tin.it>
Data: venerdì 14 luglio 2000 18.34
> > Tutti i tagli devono essere
archi di circonferenza.
>
> Forse intendi tutti i tagli curvi?
> Nel risultato che abbiamo trovato finora ci sono quattro
archi di circonferenza piu' un tratto rettilineo; credo che per
ragioni di simmetria non potrebbe essere diversamente.
ciao
paolo
Da: "Crios"
<Crios@cclinf.polito.it>
Data: venerdì 14 luglio 2000 18.34
> Forse intendi tutti i tagli curvi?
Be'... la locuzione esatta e' 'a curvatura costante'
Colgo l'occasione per spiegare la formula t*c=p (oops ho scritto
2*t*c=p...) :
un segmento elementare di bolla si comporta come una cordicella
lunga dl, sottesa da un angolo dO (leggi de-theta) e stirata da
due forze uguali ed opposte t. La componente normale t_n (l'unica
efficace) di queste ultime e' 2*t*sin(dO/2)=2*t*(dl/2R)=t*dl/R,
la pressione invece e' (p1-p2)*dl, diciamo con p1 la pressione
dalla sezione concava della bolla, indicando con m la densita'
lineare si ottiene (verso concorde tra a e t_n) :
t*dl/R - (p1-p2)*dl = m*dl*a
Che e' (circa) l'equazione che avevo scritto.