DEFINIZIONE: il lavoro in meccanica è l'energia(a) che si deve spendere affinchè una forza F sposti il suo punto di applicazione della distanza S: lavoro speso (oppure: che si acquista quando la forza F sposta il suo punto di applicazione della distanza S: lavoro acquistato).
Non sempre però si utilizza tutta la forza che si ha a disposizione per produrre lavoro. Se la forza e lo spostamento non sono sulla stessa retta (stessa direzione), allora una parte della forza si perde, oppure, a parità di forza, lo spostamento è minore.

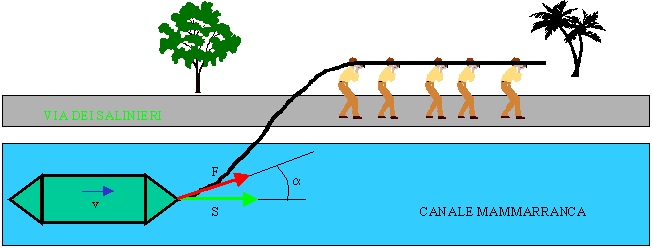
DESCRIZIONE: a Cagliari c'è un canale artificiale, detto di Mammarranca o di Terramaini, lungo un lato delle saline di Molentargius. Il canale serviva per trasportare, con le chiatte, il sale alle navi in porto, oppure alla stazione dei treni merci di Monserrato. Le chiatte venivano trascinate a braccia con una fune da operai - schiavi che marciavano su una strada parallela al canale, detta ancora oggi Via dei Salinieri.
In questa situazione la forza F e lo spostamento S sono in due direzioni ben diverse, formando fra loro un angolo a. Gli operai non solo dovevano trascinare il peso della chiatta, ma anche il peso della fune e inoltre vincere la resistenza del timone, senza il quale il natante si sarebbe piantato nelle sponde del canale.
CALCOLO: la definizione elementare di lavoro è L = F * S quando F ed S hanno la stessa direzione. Negli altri casi occorre individuare quale parte di F è davvero utile, oppure quale parte di S è nella direzione della forza F.

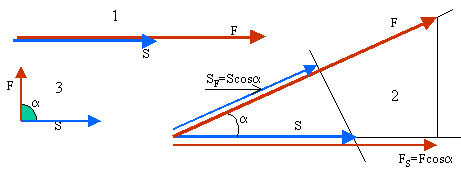
In generale sono possibili tre casi:
caso 1: F ed S sono paralleli: L = F * S;
caso 2: F ed S formano tra loro un angolo a: L = F * S_F essendo S_F la proiezione di S nella direzione di F; oppure L = S * F_S essendo F_S la proiezione di F nella direzione di S.
caso 3: F ed S formano un angolo di 90°: L = 0(b) poichè cosa = 0 (possiamo dire che non c'è forza nella direzione dello spostamento, oppure che non c'è spostamento nella direzione della forza).
AVVERTENZA: in generale una grandezza come il lavoro si calcola attraverso il "prodotto scalare" fra grandezze di tipo vettoriale. Tale prodotto, dati due vettori A e B di moduli a e b, si scrive A X B e si legge "A scalare B". Il termine scalare si riferisce a quelle grandezze che non sono vettori ma neppure "numeri" in quanto possiedono una unità di misura. Per quanto riguarda il lavoro, esso si misura nel sistema internazionale in [J] (Joule) e quindi non è un numero puro. Tuttavia poichè il lavoro non cambia, portando un carico, andando a destra o a sinistra, esso non è un vettore.
Il risultato dell'operazione prodotto scalare è c = a * b * cosa, essendo appunto a l'angolo fra i vettori A e B. Si noti che c, risultato del prodotto, è stato scritto minuscolo perchè non è un vettore.

(a) E' utile esaminare cosa accade dell'energia nel gioco degli acrobati che consiste nel far volare uno di loro per mezzo di un'asse elastica.

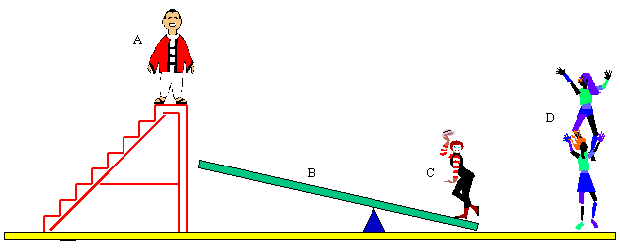
L'acrobata A salta sull'asse B lanciando in aria il collega C, il quale termina il suo volo sulla colonna D. Vediamo il bilancio dell'energia. I giocolieri mettono a disposizione l'energia potenziale posseduta da A sulla cima della scala (il valore dell'energia potenziale è dato da E = P * h, essendo P il peso e h l'altezza di caduta); l'energia potenziale si trasforma in cinetica per effetto del salto sull'asse, la quale accumula energia elastica e la restituisce per lanciare C, così in alto da consentirgli di ricadere in piedi su D.
Ci chiediamo: tutta l'energia potenziale di A è stata utilizzata? oppure ci sono perdite e quali? dove è finita l'energia dispersa?
Alla prima domanda si deve rispondere no non tutta l'energia è stata utile per svolgere l'esercizio. La risposta alla seconda domanda è un poco complessa: 1) durante i salti di A e di C una parte di energia viene ceduta all'aria; 2) l'asse continua a vibrare dopo aver lanciato C, il che significa che non ha restituito tutta l'energia che aveva accumulato. La risposta alla terza domanda è semplice e difficile: l'energia persa nell'aria e nell'asse si è trasformata in calore, ma con un aumento di temperatura non misurabile con un termometro; per convincersi bisogna ricordare che il calore è movimento.
Considerazioni: si è detto che C deve volare sufficientemente in alto da poter cadere in piedi su D. Come è possibile viste le perdite e tenendo conto che C vola più in alto di A? Il segreto è nel fatto che A deve PESARE molto di più di C (le forze in gioco sono solo i pesi), tanto che, se la colonna D è molto alta, A non è solo in cima alla scala.
(b) Supponiamo di portare un gran peso sulle spalle su una strada orizzontale: il peso è verticale e la strada è orizzontale, cioè lo spostamento è perpendicolare alla forza. In questo caso il lavoro per definizione è zero e quindi non dovremmo fare nessuna fatica nel trasportare il carico!
Ci si può chiedere dove è l'errore, visto che invece si fatica. L'errore consiste nella forza; la forza che ci consente di fare lo spostamento non è il peso, ma la forza d'attrito radente fra scarpa e terreno e tale forza è orizzontale, cioè parallela allo spostamento. Al crescere del carico cresce l'attrito e cresce purtroppo la fatica.