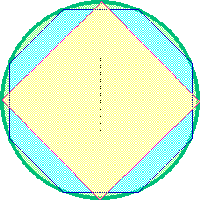
Una considerazione analoga si può fare rispetto alla retta dicendo: la retta è una circonferenza di raggio infinito. Per avere un'idea di questa affermazione basta pensare alle curve delle strade: quando la curva è "larga" è facile pensarla quasi come un rettilineo un poco particolare. E' ovvio che se la curva stradale ha un raggio infinito diventa un rettilineo.
Nella termodinamica si ha spesso a che fare con le curve rappresentative delle trasformazioni, sia teoriche che sperimentali. Dalla forma e dall'estensione delle curve si devono ricavare parametri essenziali come il calore e il lavoro in gioco. Le curve (o i diagrammi) sperimentali, cioè disegnate direttamente dalla "macchina", quasi mai sono rappresentabili con una equazione univocamente valida. Ci si trova quindi nella necessità di fare calcoli "precisi" e approssimati.
I calcoli "precisi" sono quelli di tipo differenziale, come per esempio dL = p dv, e integrale, come per esempio L = ∫ p dv; quelli approssimati sono del tipo DQ = c_v DT. I due tipi di calcolo si assomigliano quando le differenze D sono relativamente piccole. Tenendo conto che nelle applicazioni impiantistiche, approssimazioni del 2 - 3 % sono accettabili, spesso, oltre che indispensabile, è conveniente utilizzare il calcolo approssimato, purché, come detto, i D siano scelti in modo ragionevole caso per caso.

LA SCALA.
Quando si deve fare una valutazione approssimata su un diagramma, è di fondamentale importanza servirsi di una scala di rappresentazione opportuna. Se il fenomeno da studiare è di piccola entità, occorre "ingrandire" il suo diagramma, perché piccoli errori assoluti possono diventare grandi errori relativi, capaci di falsare tutto il processo.
Per esemplificare supponiamo di dover valutare il lavoro svolto da un motore misurando l'area sottesa dal diagramma tracciato su un monitor attraverso gli appositi sensori. Il diagramma deve essere trasferito su carta e ingrandito, di più se il motore è piccolo, di meno se il motore è grande.

L'IPERBOLE EQUILATERA.
Al paragrafo sulle trasformazioni termodinamiche si è visto che le isoterme, nel piano (p, v) sono rappresentate da un ramo di iperbole equilatera. Nel piano cartesiano "normale" (x, y) l'iperbole ha una equazione del tipo x y = M = costante ed è costituita da due rami nel primo e terzo quadrante se M > 0; da due rami nel secondo e quarto quadrante se M < 0 (vedi figura). In tutti i casi gli assi coordinati sono asintoti(1) per la curva.

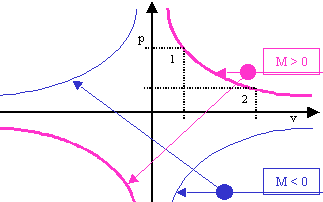
Nel campo della matematica entrambe le soluzioni sono valide. Nel campo fisico invece, poiché parlare di pressioni e di volumi minori di zero non ha senso, rimane valido solo il ramo del primo quadrante con M > 0 (la linea più spessa in rosso). L'equazione dell'isoterma è quindi p v = Z, con le condizioni p > 0 e v > 0 dalle quali segue Z > 0.
L'iperbole si può anche definire nel modo seguente: è il luogo dei punti che sottendono aree uguali. Ciò vuol dire che, presi due punti 1 e 2, risulta p₁ v₁ = p₂ v₂, risultato assolutamente ovvio proprio perché p v = costante(2). Ricordiamo anche che, nelle isoterme, tutto il calore si trasforma in lavoro, per cui risulta anche: L_1,2 = Area ( v₁ - 1 - 2 - v₂ ).
Problemi del tutto simili si pongono sia per l'adiabatica (equazione p v^k = Z ) che per la politropica (equazione p v^a = Z ).


1) Si chiamano asintoti quelle rette tali che la loro distanza dalla curva tende a zero; oppure tali da avere lo stesso punto all'infinito della curva; oppure tali da essere tangenti alla curva nel punto all'infinito. Questi tre "modi di dire" sono equivalenti fra loro.
2) Nella figura ciò non accade perché essa non è stata costruita secondo la definizione suddetta.