 |
LAVORO
ISOBARA E ISOTERMA
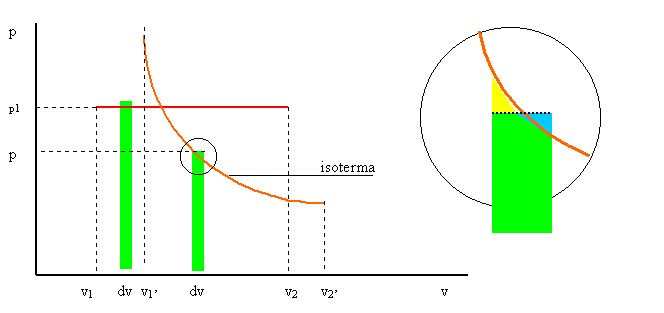
Nel piano p – v rappresentiamo una trasformazione isobara e una isoterma:
 |
Per “misurare” il lavoro eseguito lungo una trasformazione, prendiamo sull’asse dei volumi un segmento infinitesimo dv e sull’asse delle pressioni un’altezza generica p: si ottiene una superficie (in verde nella figura) di area dB = p dv.
Dimostriamo che tale area rappresenta un lavoro analizzando le unità di misura:
[dB] = [p dv] = [kg / m2 * m3 / kg] = [kg m / kg]
cioè l’area misurata nel piano p v rappresenta
proprio il lavoro [kg m] eseguito da un kg di gas.
LAVORO NELL’ISOBARA: essendo p = costante = p1 si ottiene
L = ò1,2 dL = ò1,2 p dv = p1 ò1,2 dv = p1 (v2 – v1) (2’’)
Che è l’area della superficie al disotto della
trasformazione isobara in rosso nella figura.
LAVORO NELL’ISOTERMA: se consideriamo la quota di compenso p (vedi ingrandimento a destra: il triangolo giallo ha la stessa superficie di quello azzurro), il problema si risolve come per l’isobara, ma tenendo conto dell’equazione di definizione della trasformazione (vedi l’espressione 3 nelle pagine precedenti) nella quale sia R che T sono costanti:
L = ò1,2 dL = ò1,2 p dv = ò1,2 R T dv / v = R T ò1,2 dv / v =
= R T (ln v)1,2 = R T ln(v2 / v1) (3’’)
che è appunto il risultato ottenuto in precedenza.
TRASFORMAZIONE
ADIABATICA
E’ la trasformazione per la quale risulta dQ = 0, cioè che avviene senza che il gas scambi calore con l’esterno. Ricordando che in genere il calore fornito ad un gas produce aumento di temperatura e lavoro, cioè che dQ = dU + A p dv = cv dT + A p dv, e che A R = cp - cv sostituendo si ottiene
dQ = cv dT + A p dv = 0 e quindi Q = costante
Utilizzando gli integrali indefiniti avremo:
ò
dQ = ò
cv dT + ò
A p dv = ln cost
ò
cv dT + ò
A p dv = ò
cv dT + A ò
R T dv / v = ln cost
Separando le variabili (dividendo tutto per T):
cv
ò
dT / T + A R ò
dv / v = ln cost
cv
lnT + A R lnv = ln cost
lnTcv + lnvA R = ln cost
lnTcv vA R = ln cost Tcv vA R = cost
Essendo A R = cp - cv, k = cp / cv, T = p v / R otteniamo
(p v / R) cv v cp - cv = pcv v cp – cv + cv / Rcv = pcv v cp / Rcv = cost
Estraendo la radice cv-esima dei due membri e
osservando che sia R che la radice cv-esima della costante sono
costanti, infine si ottiene
p v cp/cv = p v k = cost
che è appunto l’equazione che definisce l’adiabatica.
Questo è uno dei modi di scrivere l’equazione dell’adiabatica. Tenendo conto delle relazioni esistenti fra le variabili, si può scrivere:
p
v vk-1 = cost
pv = R T
R T vk-1 = cost
T
vk-1 = cost
ATTENZIONE: aver
scritto = ln cost anziché = cost è un semplice artificio matematico; in realtà
non serve proprio in quanto il logaritmo di una costante è ovviamente una
costante. Lo stesso vale per = cost / R.
LAVORO
ADIABATICA
Riprendiamo l’espressione del lavoro termodinamico e introduciamo per p l’equazione della adiabatica avendo posto p v k = cost = D e quindi p = D / v k = D v -k:
L
= ò
p dv = ò
D dv / v k = D ò
v –k dv =
=
D v –k+1 / (– k + 1)
L1,2
= D (v2 –k+1 – v1 –k+1)
/ (– k + 1) = D (v1–k+1 – v2–k+1)
/ (k – 1)
Questo è uno dei modi di scrivere l’equazione dell’adiabatica. Tenendo conto delle relazioni esistenti fra le variabili, si può scrivere:
D
= p1 v1 k = p1 v1 v1
k-1 = R T1 v1–k+1
= 1 / v1k-1
v2–k+1 = 1 / v2k-1
v = (D / p)1/k
L1,2
= [p1 v1 / (k
– 1)] [v1 k-1 / v1 k-1 - v1
k-1 / v2 k-1] =
=
[p1 v1 / (k
– 1)] [1 – (v1 / v2) k-1]
=
=
[R T1 / (k – 1)] [1
– (v1 / v2) k-1]
=
=
[p1 v1 / (k
– 1)] [1 – (D / p1 / D / p2) (k-1)/k]
=
=
[p1 v1 / (k
– 1)] [1 – (p2 / p1) (k-1)/k]
Tutte queste relazioni sono equivalenti fra loro: la scelta di utilizzare l’una o l’altra dipende soltanto dai dati a disposizione, cioè se si dispone dei volumi specifici si usa l’una, se dispone delle pressioni si usa l’altra e così via, a seconda della maggiore o minore comodità di calcolo. Naturalmente non si può prendere un pezzo dell’una e un pezzo dell’altra relazione!
Le stesse operazioni si possono eseguire con tutte le
altre “formule” già scritte o che scriveremo nel seguito.
ESEMPIO
Calcolare il lavoro di compressione effettuato su P = 0,5 kg di aria dalla situazione 1 (p1 = 3 atm; t1 = 22 °C) alla situazione 2 (p2 = 27 atm; t2 = 345 °C) seguendo un’adiabatica. Calcoliamo v1 e v2 usando l’equazione di stato:
v1 = R T1 / p1 = 29,27 x (273 + 22) / 30.000 = 0,2878 m3 / kg
v2 = R T2 / p2 = 29,27 x (273 + 345) / 270.000 = 0,0670 m3 / kg
Poiché D è costante possiamo trovarne il valore per esempio nel punto 1:
D
= p1 v1k = 30.000 x 0,28781,41 =
5.181 kg m / kg
L1,2
= D (v1 –k+1 – v2 –k+1)
/ (k – 1) =
=
5.181 x (0,2878-1,41+1 – 0, 0670-1,41+1) / (1,41 – 1)
= – 17.196 kg m / kg
Ltot
= L P = – 17.196 x 0,5 = – 8.598 kg m
CICLO
OTTO NEL PIANO p – v
I motori delle nostre automobili funzionano teoricamente secondo delle trasformazioni che si ripetono ciclicamente ad ogni giro (motori due tempi) oppure ogni due giri (motori quattro tempi) dell’albero motore. I motori a benzina, o meglio a carburazione, seguono un ciclo detto Otto, quelli a gasolio, o meglio ad iniezione, seguono un ciclo detto Diesel.
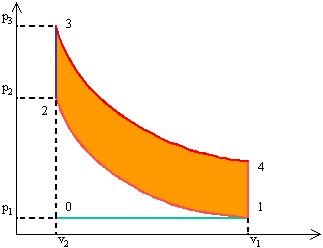
Il ciclo Otto nel piano p – v (vedi figura) contiene
due adiabatiche: compressione 1 – 2 ed espansione 3 – 4. Il rapporto r
= v1 / v2 prende il nome di rapporto di compressione e
vale mediamente r
= 10.
LAVORO DI COMPRESSIONE
All’inizio nel cilindro c’è una miscela di molta aria e poca benzina alla pressione atmosferica p1 = 1 atm e alla temperatura ambiente per esempio di t1 = 20 °C. Questa miscela viene di solito considerata in prima approssimazione come un gas ideale e si fanno i calcoli come se fosse solo aria. Supponiamo che il volume proprio del cilindro sia V = 500 cm3 = 0,0005 m3. In tale ipotesi si ha:
v1 = R T1 / p1 = 29,27 x (273 + 20) / 10.000 = 0,8576 m3 / kg
v2 =
v1 / r
= 0,8576 / 10 = 0,08576 m3 / kg
La costante in questo caso vale:
D
= p1 v1k = 10.000 x 0,85761,41 =
8.052 kg m / kg
E quindi il lavoro di compressione è:
L1,2
= D (v1 –k+1 – v2 –k+1)
/ (k – 1) =
=
8.052 x (0,8576 -1,41+1 – 0,08576 -1,41+1) / (1,41 –
1) = – 32.846 kg m / kg
Il peso (teorico!) della miscela aria – benzina (come se fosse solo aria!) vale:
P
= g
V = V / v1 = 0,0005 / 0,8576 = 0,00058 kg
E quindi il lavoro totale per una compressione è:
Ltot
= L P = – 32.846 x 0,00058 = – 19,05 kg m
Alla fine della compressione la pressione e la temperatura sono diventate:
p2
= D / v2k = 8.052 / 0,085761,41 = 257.023 kg /
m2 = 25,7 atm
T2
= p2 v2 / R = 257.023 x 0,08576 / 29,27 = 753 °K
t2
= 753 – 273 = 480 °C
LAVORO DI ESPANSIONE
Dal punto 2 al punto 3 avviene la combustione, crescono sia la pressione che la temperatura mentre il volume rimane v2. Supponiamo che sia t3 = 1.100 °C e allora:
p3
= R T3 / v3 = R T3 / v2 = 29,27 x
(273 + 1.100) / 0,08576 =
=
468.606 kg / m2 = 46,9 atm
La costante in questo caso vale:
D
= p3 v3k = p3 v2k
= 468.606 x 0,085761,41 = 14.680 kg m / kg
E quindi il lavoro di espansione è:
L3,4
= D (v4 –k+1 – v3 –k+1)
(– k + 1) = D (v2 –k+1
– v1 –k+1) (k – 1) =
=
14.680 x (0,08576 -1,41+1 – 0,8576 -1,41+1) (1,41 – 1)
= 59.884 kg m / kg
Il lavoro totale per una espansione è:
Ltot
= L P = 13.885 x
0,0005 = 29,94 kg m
Alla fine della espansione la pressione e la temperatura sono diventate:
p4
= D / v4k = 14.680 / 0,85761,41 = 18.230 kg / m2
= 18,2 atm
T4
= p4 v4 / R = 18.230 x 0,8576 / 29,27 = 534 °K
t2
= 534 – 273 = 261 °C
OSSERVAZIONI
A) In questa situazione del tutto teorica il lavoro di compressione vale – 19,05 kg m e quello di espansione 29,94 kg m, per cui si ha un guadagno (lavoro utile) di
Lut
= 29,94 – 19,05 = 10,89 kg m
B) I risultati ottenuti sono del tutto teorici, senza quasi nessun aggancio alla realtà costruttiva: si tratta di puri esempi di carattere matematico, utili soltanto per mostrare l’uso dell’algebra in campo impiantistico.
ENTROPIA
Si chiama entropia una “cosa” che misura la degradazione dell’energia, nel senso che al crescere dell’entropia diminuisce la nostra possibilità di utilizzare il calore. Nel nostro universo l’entropia è destinata a crescere all’infinito, almeno secondo le nostre attuali conoscenze.
L’entropia è definita dalla relazione:
dS = dQ / T
Integrando in modo indefinito si ottiene:
DS = ò dQ / T
Note le leggi di variazione di Q e di T si può passare alle espressioni di Q e di T. Ricordando che
dQ
= dU + A p dv = cv dT + A p dv
DS
= ò
(cv dT + A p dv)
/ T = cv ò dT
/ T + A ò
p dv / T
possiamo calcolare la variazione di entropia nelle prime trasformazioni:
isocora:
essendo dQ = cv dT
resta DS
= cv ò
dT / T = cv lnT (1’’’)
isobara:
essendo dQ = cp dT
resta DS
= cp ò
dT / T = cp lnT
(2’’’)
isoterma: essendo dT = 0 e quindi T = cost p = R T / v resta
DS
= A ò
p dv / T = A R ò dv
/ v = A R lnv = (cp - cv) lnv
(3’’’)
ESEMPI
Essendo per l’aria cp = 0,241 Cal / kg °K,
cv = 0,172 Cal / kg °K, R = 29,27 kg m / kg °K, calcolare:
1) isocora: la variazione di entropia sviluppata quando P = 4 kg di aria vengono riscaldati a volume costante da t1 = 30 °C a t2 = 560 °C. Si ha:
DS
= S2 – S1 = cv lnT = cv ln (T2
/ T1) =
=
0,172 ln [(560 + 273) / (30 + 273)] = 0,1739 Cal / kg °K
Per il peso P e per il salto di temperatura t2 – t1 si avrà:
DStot
= P DS
Dt
= 5 x 0,1739 x (560 – 30) = 461
Cal
ATTENZIONE: l’operazione 560 / 30 = 18,67 è diversa dall’operazione (560 + 273) / (30 + 273) = 2,7491!!!!!! Cioè aggiungere o togliere qualcosa al numeratore e al denominatore di una frazione ne fa cambiare il valore.
Invece il salto di
temperatura è lo stesso sia in °C che in °K.
2) isobara: la variazione di entropia sviluppata quando P = 6,5 kg di aria alla pressione costante p = 4 atm vengono riscaldati da t1 = 50 °C a t2 = 400 °C . Si ha:
v1 = R T1 / p = 29,27 x (273 + 50) / 40.000 = 0,2364 m3 / kg
v2 = R T2 / p = 29,27 x (273 + 400) / 40.000 = 0,4925 m3 / kg
DS
= S2 – S1 = cp lnT = cp ln (T2
/ T1) =
=
0,241 ln [(400 + 273) / (50 + 273)] = 0,1769 Cal / kg °K
Per il peso P e per il salto di temperatura t2 – t1 si avrà:
DStot
= P DS
Dt
= 6,5 x 0,1769 x (400 – 50) = 403 Cal
3) isoterma: la variazione di entropia sviluppata quando P = 29 kg di aria alla temperatura costante t = 90 °C vengono decompressi da V1 = 16 m3 a V2 = 40 m3. Si ha:
v1
= V1 / P = 16 / 29 =
0,5517 m3 / kg
v2 = V2 / P = 40 / 29 =
1,3793 m3 / kg
DS
= S2 – S1 = (cp
- cv) lnv = (cp - cv) ln (v2 / v1)
=
=
(0,241 – 0,172) x ln (1,3793 / 0,5517) = 0,0632 Cal / kg °K
Per il peso P e per il salto di temperatura t2 – t1 si avrà:
DStot
= P DS
Dt
= 29 x 0,0632 x (273 + 90) = 666
Cal
ENTALPIA
L’entalpia è l’energia totale posseduta dal gas, misurata come se fosse tutta sotto forma di calore. Poiché l’energia totale può provenire da una variazione della temperatura (rappresentata dalla variazione di energia interna), da una variazione della pressione e da una variazione del volume del gas, l’entalpia sarà espressa dalla relazione:
dh = dU + A (d p v) = cv dT + A v dp + A p dv
dalla quale, ricordando le espressioni trovate in precedenza, si ricava:
Dh
= cv ò dT
+ A ò v
dp
+ A ò
p dv =
=
cv ò
dT + A ò
R T dp / p
+ A ò
R T dv / v
Dividendo entrambi i membri per T si ottiene:
Dh = cv ò dT / T + A R ò dp / p + A R ò dv / v =
= cv
lnT + (cp - cv) lnp + (cp - cv) lnv
ESEMPIO
Essendo per l’aria cp = 0,241 Cal / kg °K, cv = 0,172 Cal / kg °K, R = 29,27 kg m / kg °K, calcolare la variazione di entalpia quando P = 360 kg di aria vengono riscaldati in modo che la temperatura varia di 290 °C e la pressione varia di 16 atm, partendo dalle condizioni standard.
Le condizioni standard per l’aria sono (vedi Manuale Colombo): p1 = 1 atm; v1 = 0,7735 m3 / kg per cui risulta
t1
= p1 v1 / R – 273 = 10.330 x 0,7735 / 29,27 – 273 =
0 °C.
Quindi le condizioni finali sono: p2 = (1 + 16) atm; t2 = 290 °C per cui risulta
v2 = R T2 / p2 = 29,27 x (273 + 290) / 170.000 = 0,0969 m3 / kg
La variazione di entalpia è quindi:
Dh = cv lnT + (cp – cv) lnp + (cp – cv) lnv =
=cv
ln (T2 / T1) + (cp – cv) ln (p2
/ p1) + (cp
– cv) ln (v2 / v1) =
=
0,172 ln (563 / 273) + (0,241 – 0,172) ln
(170.000 / 10.000) + (0,241 – 0,172) ln (0,0969 / 0,7735) = 0,1767 Cal / kg
Tenendo conto del peso dell’aria avremo:
Dhtot
= P Dh
= 360 x 0,1767 = 63,6 Cal