PAGINETTA DI STORIA
La matematica è come un grande edificio, composto di più piani, ciascuno contenente appartamenti destinati ad usi diversi, abitato da persone di diverso livello culturale.
Al piano terreno c'è l'aritmetica e nessuno ha difficoltà a raggiungerlo, anche se poi molti confondono questa parte dell'edificio con tutto l'edificio: non conoscendo le scale per salire ai piani superiori si convincono che la matematica è tutta lì.
Al primo piano c'è la geometria, ma per entrarci bisogna passare da un grande atrio nel quale si aprono molte porte su ciascuna delle quali un cartello avverte sulle ipotesi che bisogna accettare per aprirla.
Al secondo piano c'è l'algebra: un lungo corridoio inizialmente stretto e buio, poi sempre più ampio e luminoso, ornato di fiori e quadri, ma anche disseminato di ostacoli e trabocchetti: percorrerlo tutto è difficile e avventuroso. Su questo corridoio si aprono numerose porte che danno su appartamenti abitati da professionisti di diverse specializzazioni.
Al termine di questo corridoio, per chi riesce a percorrerlo tutto, c'è una torre di vetro e marmo e avorio che ha una scala che permette di scendere verso il piano della geometria e di salire verso gli altri piani.
Dalla torre si può salire, con una scala stretta e ripida, al terzo piano che contiene la geometria analitica e, da qui, con una rampa dolce, si sale all'attico, ampio, luminoso, panoramico, aperto verso il cielo, che contiene la matematica sublime, in un unico ambiente, solo scandito da paraventi di seta e d'oro, intitolati a limiti e derivate e differenziali e integrali. Qua e là ci sono delle nicchie riservate a personalità di grande importanza, che solo raramente si fanno vedere.
Ecco, questo è il mio modo di vedere la matematica. E io sono entrato qualche volta, nell'attico, di sfuggita, come un turista frettoloso.
Chi ha costruito questo edificio?
Hanno cominciato egiziani e babilonesi e greci nell'antichità, hanno proseguito gli arabi nel medioevo e poi ....
Poi si può fare qualche nome come Galileo, Torricelli, Cavalieri, Fermat, Newton, Leibniz, Bernoulli, Carnot, Cauchy, Mac Laurin, Cartesio, e altri e altri ancora. Ma l'edificio non è finito, ci sono lavori continui di manutenzione e aggiornamento e abbellimento.
QUALCHE NOTIZIA
Ho trovato in internet una pagina veramente interessante intitolata "Il calcolo inifinitesimale dalle origini ai nostri giorni" pubblicato nel sito del Liceo scientifico Mancini di Avellino. Qui di seguito ne riporto una piccola parte poiché il documento è veramente lungo. Io mi sento di consigliare a tutti i miei lettori di andare a vederlo nell'originale.
Introduzione
Sotto questo nome si comprendono insieme il calcolo differenziale ed il calcolo integrale. Il calcolo integrale ci consente di ottenere la
lunghezza di una curva, il volume di un solido, l’area di una superficie. Il calcolo differenziale risolve questioni quali la tangente ad una curva, gli estremi di una funzione, la velocità istantanea di un punto materiale.
Non è possibile fissare con precisione le origini del calcolo differenziale; tuttavia può affermarsi con sicurezza che il suo sorgere fu preparato dagli studi che si svilupparono nel secolo XVII intorno ai problemi della tangente ad una curva (Fermat, Cartesio, Torricelli, Roberval, Barrow), della velocità istantanea di un punto materiale (Torricelli, Roberval e dei massimi e minimi delle funzioni Fermat). Il merito di avere fondato il calcolo differenziale con tutta la sua generalità e di averne messa in evidenza la grande importanza, spetta ad Isacco Newton ed a Goffredo Guglielmo Leibniz.
Newton elaborò il metodo delle flussioni che è una forma di calcolo differenziale. Rigettando l’idea che le grandezze geometriche siano costituite da parti infinitamente piccole, egli concepì tali grandezze come prodotte da un moto continuo, precisamente le linee come prodotte dal moto continuo di un punto, le superfici dal moto continuo di una linea, e così via .
Dette fluenti le grandezze generate, chiamò flussioni le velocità con cui esse vengono formate, ed osservò che, considerando intervalli di tempo uguali, ma piccoli quanto si vuole, le flussioni diventano proporzionali agli accrescimenti corrispondenti delle fluenti. Basandosi sulla considerazione del limite del rapporto di due quantità evanescenti, insegnò a determinare le flussioni, conosciute che siano le fluenti; e questa parte del suo metodo corrisponde al nostro calcolo differenziale. Leibniz, ammesso esplicitamente il principio di continuità(1), procedette, non per flussioni di linee, ma per differenze di numeri, introducendo le differenze infinitesime dx e dy di due punti vicinissimi di una curva. Ciò che oggi noi chiamiamo derivata non è altro che il rapporto dy / dx di Leibniz, e corrisponde alla flussione di Newton. L’elemento fondamentale del metodo di Leibniz é l’introduzione del concetto di differenziale che è un infinitesimo. Tuttavia che cosa fosse precisamente nel pensiero di Leibniz l’infinitesimo, non è facile comprendere dalla lettura delle sue opere. Sembra che egli ammettesse l’esistenza degli infinitamente piccoli come infinitesimi attuali, ma qualche volta si ha la sensazione che egli considerasse questi infinitesimi semplicemente come quantità finite indefinitamente decrescenti(2). Comunque sia, l’algoritmo differenziale da lui creato trionfò completamente su quello delle flussioni di Newton; ed a tale trionfo contribuì in larga parte la felice scelta dei simboli, alla quale il Leibniz attribuì grandissima importanza. Nonostante i brillanti risultati ottenuti nell’applicazione dei procedimenti di Leibniz ai più svariati problemi della matematica, restava alla base della teoria una grande incertezza ed oscurità e le menti più acute erano assillate dal desiderio di precisare i principi fondamentali, liberandoli da ogni considerazione metafisica.
La matematica greca urtò quasi dai suoi inizi contro il problema dell’infinito. Questo problema si presentò quando furono scoperte le cosiddette linee incommensurabili(3):
un numero intero di volte tanto nel lato quanto nella diagonale di un qualunque quadrato"
Un solo rimedio è possibile, di fronte alla sconcertante scoperta delle linee incommensurabili: l‘annichilimento del punto, che viene ridotto ad una entità evanescente, cioè senza dimensioni: privo di
lunghezza, privo di larghezza, privo di altezza. Si tratta del famoso punto geometrico, che siamo avvezzi a considerare fin dai primi anni di scuola.
Col punto senza dimensioni e con le conseguenti concezioni della linea senza larghezza e della superficie senza spessore la geometria si distacca dalla materia e si rivolge agli enti geometrici idealizzati, sui quali opera con quella precisione che costituisce il presupposto della vera matematica.
Ecco dunque l’infinito entrare nella matematica greca: l’infinitamente grande (numero di punti su un tratto di linea) ed al tempo stesso l’infinitamente piccolo (i singoli punti sulla linea, che pur non avendo dimensioni sono tuttavia entità).
I matematici greci, di fronte ai problemi dell’infinito, si misero ben presto in posizione di difesa. Di difesa soprattutto del rigore matematico, della precisione, dell’esattezza dei ragionamenti, che l’anomalo infinito matematico rendeva talvolta vacillante, ponendo il matematico di fronte a paradossi, abusi, errori.
L’infinito si presentò soprattutto in due questioni:
1) nella determinazione del rapporto tra due grandezze, ad esempio geometriche, quando le grandezze stesse sono incommensurabili (come ad esempio per il lato e la diagonale di un qualsiasi quadrato);
2) quando si vogliono
paragonare tra loro le estensioni di due superfici o di due solidi.
La cosa è facile per i poligoni nel piano e per i prismi nello spazio.
Ma non per tutte le figure piane è possibile mettere in evidenza la loro equivalenza scomponendole in un numero finito di parti finite a due a due uguali. Per raggiungere lo scopo dovremmo suddividere
le figure in infinite parti infinitamente piccole. Sarà
il calcolo infinitesimale a percorrere questa via: ne troviamo robusta anticipazione in Democrito ed in Archimede e poi assai più tardi, attraverso Galileo Galilei, in Bonaventura Cavalieri ed Evangelista Torricelli e nel secolo XVII giungeremo fino alla fondazione di detto calcolo con Leibniz e Newton.
Ma la matematica greca ufficiale non percorse questa via, e, per evitare l’uso diretto dell’infinito, evidentemente pericoloso per il rigore matematico, escogitarono geniali, ma al tempo stesso paralizzanti teorie, che si mossero in ambito perfettamente rigoroso.
Fu il matematico Eudosso di Cnido il maestro dei maestri in questo campo e per questo motivo è stato definito il più grande imbrigliatore dell’infinito.
Egli rispose alla prima esigenza (determinazione del rapporto tra due grandezze incommensurabili) mediante la teoria delle proporzioni, che ritroviamo poi esposta nel libro V degli Elementi di Euclide; rispose alla seconda esigenza con quel metodo che nel seicento chiamarono metodo di esaustione e che troviamo applicato nel libro XII degli stessi elementi di Euclide.
Sia con la teoria delle proporzioni, sia col metodo di esaustione, Eudosso evitò l’uso diretto dell’infinito, ma non potè certo evitarne l’uso indiretto: ad ogni modo, attraverso i rigidi schemi da lui escogitati fornì una trattazione perfettamente rigorosa.
In questo modo la matematica greca vinse la sua battaglia contro l'infinito: evitandolo fin dove possibile.
La scoperta delle linee incommensurabili e la concezione degli enti geometrici idealizzati presentarono gravi questioni ai matematici.
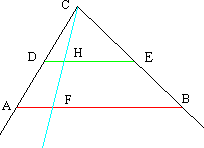
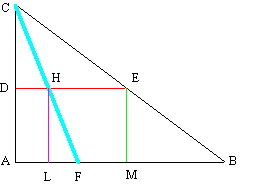
Sia dato il segmento AB. Dal punto C tracciamo le rette CA e CB congiungenti C con gli estremi del segmento AB. Prendiamo il punto medio D di AC e per esso tracciamo la parallela DE ad AB, fino a tagliare nel punto E la retta CB. Otteniamo il segmento DE che è la metà del segmento AB.
Ci domandiamo ora: quanti punti contiene il segmento AB? Secondo la concezione degli enti geometrici idealizzati dobbiamo rispondere: AB contiene infiniti punti in quanto sappiamo che tra due punti qualsiasi possiamo inserire almeno un altro punto. E se ci domandiamo quanti punti contiene il segmento DE dobbiamo rispondere che ne contiene infiniti.
Siccome AB è doppio di DE verrebbe di pensare che gli infiniti punti di AB debbano essere il doppio degli infiniti punti di DE. Il senso comune ci indurrebbe a stabilire un confronto tra i due infiniti con netto vantaggio dell’infinità dei punti di AB.
Ma ora possiamo mettere in evidenza un fatto piuttosto sconcertante: i punti del segmento AB sono tanti quanti sono i punti del segmento DE.
Per dimostrarlo, consideriamo un generico punto F di AB e congiungiamolo con C: la retta FC taglia il segmento DE in un punto H. Possiamo dire che al punto F di AB corrisponde il punto H di DE. E poiché possiamo ripetere la costruzione per tutti i punti del segmento AB diremo che possiamo stabilire un corrispondenza tra tutti i punti di AB ed i punti di DE: più precisamente ad ogni punto di AB corrisponderà un solo punto di DE.
Si osserva pure che ad ogni punto di DE corrisponde un solo punto di AB. Abbiamo stabilito una corrispondenza biunivoca tra i punti del segmento AB ed i punti del segmento DE.
Quindi i punti del segmento AB sono tanti quanti sono i punti del segmento DE.
Il seguito dell'articolo è nel sito citato più su.
NOTE
(1) Il principio di continuità è "intimamente contraddittorio": infatti mentre da una parte si ammette che fra due punti qualunque A e B di una retta ci sono infiniti punti, per cui partendo da A è impossibile raggiungere B, dall'altra si ammette che si possa "saltare" da un punto all'altro trasportati da una "cosa" chiamata "tempo" (a sua volta costituito di infiniti istanti), per cui si può pensare a punti dotati di velocità (flussione per Newton). Da un punto di vista strettamente geometrico, e quindi statico, la continuità è senza significato (rifiutata quindi dai geometri greci); diventa comprensibile, e anzi indispensabile, nel nostro universo che è un "continuo divenire" che non conosce la staticità (vedi l'articolo cinematica introduzione B).
(2) L'infinitesimo attuale indica l'esistenza "concreta e materiale" di una quantità estremamente piccola ma poi non più divisibile, irraggiungibile solo perché ci mancano gli strumenti adatti: la cosa è analoga in un certo senso all'esistenza delle stelle perché sappiamo che esistono, che sono fatte di materia, ecc. ma non possiamo raggiungerle (per ora?) perché ci manca la nave adatta.
Dire che l'infinitesimo è una quantità finita indefinitamente decrescente significa dire che esso è una costruzione puramente mentale senza alcun riscontro nella realtà fisica: è come se noi dicessimo che le stelle non esistono perché non possiamo raggiungerle e quelle che noi vediamo sono immagini mentali.
(3) Nel linguaggio comune incommensurabile è una cosa così grande "che non si può misurare". In matematica, in particolare in geometria, incommensurabili sono due cose "che non si possono misurare l'una con l'altra". Per esempio: a) la diagonale di un quadrato non si può misurare usando la stessa unità di misura del lato (è questo il significato della frase in blu); b) la circonferenza non può avere la stessa unità di misura del raggio; c) un quadrato e un cerchio non possono avere la stessa area (problema della quadratura del cerchio); ecc. Tutto ciò deriva dal fatto che per passare dall'uno all'altro elemento si devono adoperare i numeri irrazionali derivanti dall'estrazione di radici oppure numeri "strani" come p. Infatti si ha:
a) per il teorema di Pitagora d2 = l2 + l2 = 2 l2 e quindi d = l (2)1/2;
b) c = 2 p r;
c) l2 = p r2.
N. B. queste note sono mie.