PROGETTO DI UN ALBERO DI TRASMISSIONE
(IN ELABORAZIONE)
Occorrono le conoscenze del capitolo di Meccanica.

PRIMA PARTE          SECONDA PARTE          TERZA PARTE

Un albero A - B, sostenuto da due bronzine alle estremità, porta una ruota dentata C che trasmette una potenza N alla velocità di n giri al minuto. Redigere una relazione sui problemi che si devono affrontare per rendere sicuro l'albero.

                

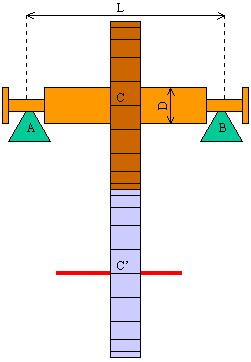
E' intuitivo che l'albero deve resistere contemporaneamente a due sollecitazioni: 1) quella dovuta al peso proprio e al peso portato dovuto alla ruota (o alle ruote) calettata su di esso; 2) quella che, provenendo da un altro organo meccanico (ruota C'), provoca il movimento rotatorio dell'albero stesso e in funzione della quale asse e ruota vengono costruite ed usate.

PRELIMINARI

A) AZIONE FLETTENTE

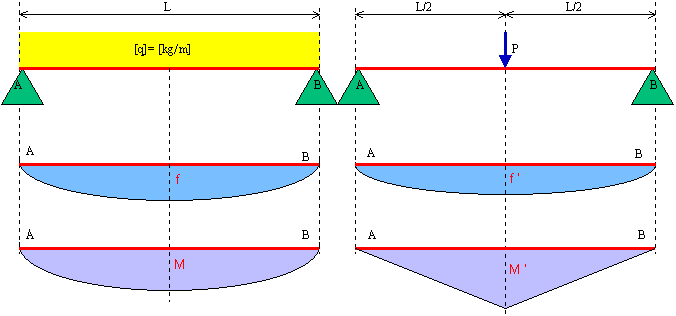
1) Per studiare le condizioni statiche e dinamiche di lavoro dell'asse procediamo alla schematizzazione della situazione fisica reale. Perciò riduciamo l'albero al suo asse geometrico, e quindi senza peso, semplicemente appoggiato ai suoi estremi e soggetto ad un carico q uniformemnte distribuito su tutta la lunghezza, rappresentante del peso proprio. Sotto l'azione di q l'asse A - B si deforma secondo un arco di circonferenza del quale AB è una corda. La freccia massima è in mezzeria e vale:
f_m = (5 / 384) (q l⁴ / E J)         (1)
nella quale E è il modulo di Young (per l'acciaio E = 21.000 kg / mm²) e J è il momento di inerzia della sezione rispetto all'asse neutro baricentrico, cioè in questo caso rispetto ad un diametro orizzontale, che vale
J = p D⁴ / 64         (2)
Sull'albero però agisce anche la ruota C di peso P distribuito lungo una parte dell'asse. La presenza di P modifica la situazione di deformazione in funzione dello spessore della ruota e della sua posizione rispetto agli appoggi. Supponendo che la ruota sia al centro di A - B e di spessore così piccolo da poterlo considerare concentrato in mezzeria, la freccia aggiuntiva massima al centro vale
f '_m = (8 / 384) (P l³ / E J)         (3)
Finché l'albero è fermo deve resistere soltanto a queste due azioni. Il diagramma del momento flettente per il carico q è parabolico con il massimo al centro di valore(*)
M = q l² / 8         (4)
e valore zero sugli appoggi. Per il carico concentrato P il diagramma è triangolare con valore massimo
M ' = P l / 4         (5)
e ancora zero sugli appoggi.



2) Queste considerazioni si modificano in modo sostanziale quando si tiene conto dei seguenti fatti:
a) l'albero non appoggia su un punto del perno, ma lungo un tratto di generatrice del cilindro che costituisce l'albero, anzi meglio su una sola parte di tale generatrice in quanto sia l'albero che il cuscinetto sono deformati: ciò comporta notevoli differenze nel regime di distribuzione delle forze esterne e delle reazioni dei vincoli (vedi un problema analogo in Progetto di un albero motore).


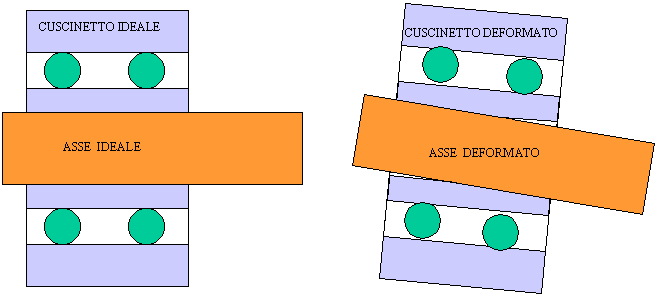
(NON E' FACILE RAPPRESENTARE LA DEFORMAZIONE!)

b) l'albero non è fermo ma in rotazione più o meno rapida, per cui si deve tener conto delle sollecitazioni dinamiche che rendono più complicato il problema.
c) lo stato di sforzo principale non è dovuto al momento flettente ma al momento torcente derivante dall'impiego funzionale della ruota come organo di trasporto di forze tangenziali.

B) AZIONE TORCENTE

a) La sollecitazione semplice di torsione si ottiene per esempio quando un cilindro, tenuto fermo ad una estremità, viene fatto ruotare applicando all'altro estremo una coppia di forze tangenziali (vedi figura). In modo banale è l'azione che si esercita sul volante dell'automobile per cambiare direzione.
Il momento della coppia agisce secondo l'asse del cilindro facendo avvolgere le fibre le une sulle altre come accade ai fili delle funi. Si sviluppano così tensioni interne tangenziali, cioè giacenti sulle sezioni normali all'asse e tendenti a far ruotare la sezione S' rispetto alla sezione contigua S''. In tal modo i diametri D' e D'' inizialmente paralleli e verticali si dispongono secondo due direzioni inclinate fra loro dell'angolo
g = g' - g''
Si definisce angolo di torsione l'angolo di cui ruotano due sezioni distanti 1 m fra loro.
b) Lo sforzo di compressione si esprime con la legge di Hooke
s = E e         (6)
essendo e l'accorciamento di una fibra lunga 1 m. In modo analogo si definisce lo sforzo tangenziale dovuto alla torsione
t = G g         (7)
nella quale G è il modulo di elasticità tangenziale di significato simile a quello di E. Ricordando che fra E, G ed m (coefficiente di Poisson o di contrazione trasversale) esiste la relazione
G = m E / 2 (1 + m)         (8)
e che per l'acciaio m = 10 / 3, risulta
G / E = m / 2 (1 + m) = 10 / 3 / 2 (1 + 10 / 3) = 0,385
dalla quale si ricava
G = 0,385 E = 0,385 x 21.000 = 8.100 kg / mm²         (9)
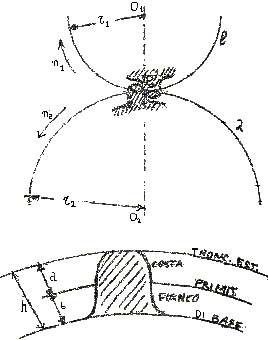
c) Se consideriamo, in un cilindro di raggio R soggetto a torsione, un punto P distante R_x dal centro (vedi figura) la tensione tangenziale in quel punto vale, essendo J_p il momento d'inerzia polare:
t_x = M_t R_x / J_p = F_t R R_x / J_p         (10)



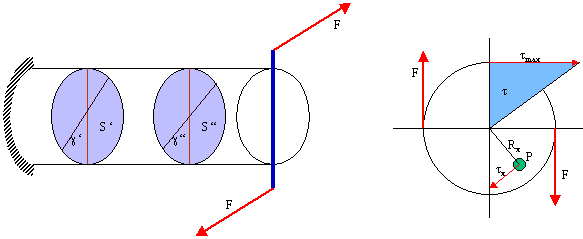
dalla quale si ricava che t_x è proporzionale alla distanza R_x di P dal centro, per cui la t_max è in corrispondenza della periferia della sezione, mentre al centro la tensione tangenziale vale zero. E' evidente l'analogia con la formula che esprime la sollecitazione s di flessione.
d) di tale distribuzione delle t possiamo approfittare rendendo gli alberi cavi, cioè vuoti all'interno, quando il loro diametro è sufficientemente grande(**). Infatti così facendo si toglie il nocciolo poco sollecitato, diminuendo il peso proprio degli organi da mettere in rotazione e di conseguenza la loro freccia e inerzia.
e) Per le sezioni circolari l'angolo di torsione fra due sezioni distanti l vale:
Q = M_t l / G J_p         (11)
mentre la condizione di resistenza impone che
t_max = M_t R / J_p £ t_amm
Nella pratica si impone che la tensione tangenziale ammissibile sia una frazione di s_amm e cioè:
t_amm = (4 / 5) s_amm         (12)
il che significa che i materiali, compreso l'acciaio, sono meno resistenti a torsione che non a flessione.

C) FORZA RADIALE

Oltre che delle forze P e q occorre tener conto anche della forza radiale F_f, cioè della componente lungo O₁ - O₂ della forza F che si trasmette fra i denti a contatto. La forza F_f si aggiunge al peso proprio della ruota, facendo aumentare il valore del momento flettente e della freccia. Ricordando che di solito si parte dal valore della potenza in CV, si ottiene immediatamente il valore della forza tangenziale F_t che è quella che produce la rotazione:
F_t = M_t / R = 716.200 N / n R [kg]         (13)
e da F_t si ricava la forza F agente fra i denti lungo la retta d'azione
F = F_t / cosq
e di conseguenza quello della forza radiale
F_f = F senq = F_t tangq



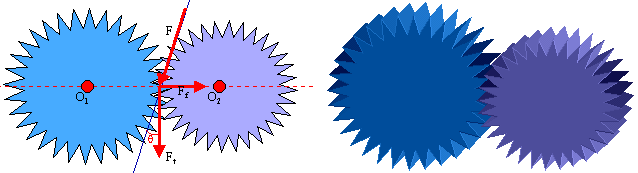
Quindi noto q, angolo di inclinazione della retta d'azione in base alle tabelle sulle ruote dentate, sono note le forze F, F_t, F_f. Il momento flettente e la freccia dovute a F_f sono dello stesso tipo di quelle dovute al peso P.

D) VELOCITA' CRITICA

a) Come si è detto, per effetto del peso proprio q dell'albero, del peso P della ruota calettata, della forza radiale F_f l'albero si deforma assumendo in prima approssimazione l'andamento di un arco di cerchio. Per effetto della rotazione l'asse così deformato descrive un fuso intorno all'asse ideale costituito dall'orizzontale passante per i centri dei supporti. L'apertura a del fuso non è costante ma crescente al crescere della velocità n di rotazione, poiché al crescere di n cresce la forza centrifuga, cioè quella forza che tende ad allontanare le masse dal centro di rotazione. Ricordando che l'accelerazione centripeta vale a_c = v² / R_E essendo R_E il raggio di rotazione del punto E che ruota alla velocità v, la forza centrifuga che ne consegue vale:
F_c = - (P / g) v² / R_E [kg]         (14)
essendo P il peso del corpo in movimento e quindi P / g la sua massa. Il segno negativo sta ad indicare che la forza centrifuga è diretta nel verso opposto dell'accelerazione, cioè dal centro verso l'esterno della circonferenza percorsa. Esprimendo F_c in funzione della velocità angolare w e del numero di giri n si ottiene:
F_c = - (P / g) v² / R_E = - (P / g R_E) (2 p R / T)² = - (P / g R_E) (w R)² = - P w² R / g =
= - (P / g R_E) (2 p R n / 60)² = - (P / g) (4 p² n² R_E / 3.600)         (15)



b) Questa forza centrifuga F_c si sviluppa per ogni particella di massa m. Per ottenere la forza centrifuga complessiva, occorre tener conto di tutta la massa in movimento, considerando le distanze dei singoli punti - massa dall'asse di rotazione. Non è qui il caso di fare tutta la trattazione analitica del problema, complicato anche dal fatto che il fuso descritto da un asse è disturbato dal fuso descritto dall'asse compagno, cioè quello che porta la ruota ingranata con quella in esame. In pratica si usa la formula di Dunkerley che pone un limite alla velocità di rotazione, imponendo che essa non superi un preordinato valore di velocità v_c, detta critica, in funzione della somma delle frecce indotte dai carichi statici. Infatti si dimostra che se v < v_c è scongiurato il pericolo che il fuso si apra sempre più sino a che l'albero si rompe.
Si pone quindi
n £ (1 / 2 ÷ 1 / 4) n_c         (16)
nella quale n_c è il numero di giri critico (quindi la velocità critica periferica vale v_c = 2 p R n_c / 60) dato dall'espressione
n_c = 1.000 / (S f_i)^1/2         (17)
dove (S f_i)^1/2 è appunto la somma delle frecce statiche viste in precedenza.


(*) Dimostriamo la correttezza di questo risultato. Per farlo mettiamo un asse x con origine in A e orientato verso B. Il carico totale vale Q = q l e lo si può pensare applicato in mezzeria poiché la distribuzione è uniforme e quindi la mezzeria è il suo baricentro. Le reazioni sono uguali e valgono ciascuna V_A = V_B = Q / 2 = q l / 2. Il momento flettente corrente ha l'espressione, da sinistra verso destra (il momento vale sempre forza per distanza!):




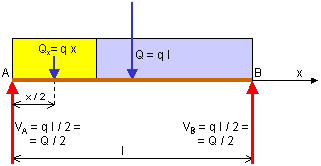
M_1x = V_A x = q l x / 2
per effetto della reazione V_A. Ma tra A e il punto x agisce anche il carico V_x = q x che ha il baricentro nel punto di ascissa x / 2 e ha braccio ancora x / 2. Il segno del momento è però negativo e quindi avremo:
M_2x = - q x (x / 2) = - q x² / 2
Il momento flettente totale vale:
M_x = M_1x + M_2x = q l x / 2 - q x² / 2
In mezzeria x = l / 2 e quindi sostituendo
M_x = q l x / 2 - q x² / 2 = (q l / 2) (l / 2) - q (l / 2)² / 2 = q l² / 4 - q l² / 8 = q l² / 8
(**) Naturalmente si deve aumentare il diametro in modo che la corona circolare rimanente sia in grado di sopportare tutta l'azione torcente.