TERZA PARTE
(IN ELABORAZIONE)
Occorrono le conoscenze del capitolo di Meccanica.
PRIMA PARTE SECONDA PARTE TERZA PARTE
Per azionare un martello pneumatico lungo una strada asfaltata si utilizza un compressore dotato di motore Diesel. Il compressore eroga aria a 9 atmosfere con portata di 120 kgm / h. La massa battente è di 6 kgm e il ritmo 20 colpi al minuto.
Determinare la massa, la forma e le dimensioni del volano adatto al lavoro descritto.
ALCUNI ESEMPI DI CALCOLO DEL MOMENTO DI INERZIA.
A) INTEGRAZIONE GRAFICA
Data la funzione fx (blu nella figura) della quale non si conosce l'equazione(1) è possibile eseguire una operazione grafica, detta integrazione grafica, che fornisce il valore dell'integrale definito, fra due valori a e b, della funzione y = fx. Il valore così trovato è soggetto ad alcune limitazioni che vedremo più avanti. L'approssimazione dipende dalla bontà dell'esecuzione grafica nonché dalla pazienza dell'operatore.
Il procedimento è il seguente:
1) in un piano appropriato, dipendente dal problema che si affronta (per esempio il piano p - v se si tratta di termodinamica), si disegna in opportuna scala, sia orizzontale che verticale(2), il diagramma della funzione y = fx.
2) si divide la funzione in strisce verticali (ad esempio di uguale ampiezza): linee nere tratteggiate verticali.
3) si mandano le linee mediane di ciascuna striscia sino ad incrociare la funzione: linee rosse (punti 1, 2, 3, ...).
4) dai punti 1, 2, 3, ... si mandano le orizzontali sino all'asse y (punti come 6' e 11'): linee verdi.
5) preso un punto O a piacere (polo di integrazione) lo si congiunge con i punti individuati prima (ad esempio O - 6', O - 11'): linee nere.
6) da un punto a piacere del margine sinistro della prima striscia si manda una parallela 1' alla prima congiungente O - 1' sino ad incrociare il margine destro della stessa striscia: linea viola.
7) dall'estremo destro di 1' si manda una parallela a O - 2' sino ad incrociare il margine destro della seconda striscia: linea viola.
8) si costruiscono così i segmenti 1', 2', 3', ..., 11'.
9) il segmento F è l'integrale definito da a a b della funzione, da leggere in opportuna scala.
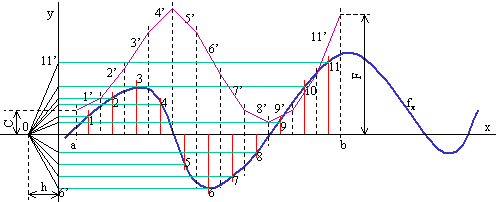
Il valore di F dipende da numerosi fattori:
1) dalla quota C, che è la costante di integrazione.
2) dalla posizione del polo di integrazione: cambiando h cambia l'inclinazione dei segmenti 1', 2', 3', ..., 11'.
3) dalle scale di rappresentazione: cambiando le scale cambia l'ampiezza delle strisce.
Il valore di F rappresenta l'area sottesa dalla funzione, cioè F = y * fx e quindi [F] = [y * fx].
Se l'orizzontale è in scala 1:p e la verticale in scala 1:q il risultato va moltiplicato: F' = (p * q) F.
Tenendo conto anche della distanza h si ha la scala di rappresentazione:
1 cm = h * p * q [y * fx]
ESEMPIO
Asse x: 1 cm = 23 kg m; asse y: 1 cm = 8 m / s; polo di integrazione: h = 11 cm; F = 16 cm; C = 4 cm
Il valore di F in modulo e unità di misura(3) è:
F = 23 x 8 x 11 x (16 - 4) = 24.288 [kg m m / s] = 24.288 [kg m2 / s]
B) MOMENTO DI INERZIA DI MASSA DI UN DISCO
Si abbia un disco di un materiale con peso specifico g, raggio R e spessore h. Consideriamo la porzione infinitesima di corona di raggi r e r + dr compresa fra gli angoli a e a + da di spessore h (segmento marron nella figura). Tale segmento solido ha in prima approssimazione(4) volume:
dV = h r da dr
nella quale r da è la lunghezza dell'arco medio della corona circolare.
Il peso del segmento infinitesimo, applicato nel baricentro G, è dP = g dV e la sua massa:
dm = g dV / g = g h r da dr / g = (g h / g) r da dr
La distanza di G dall'asse n-n è y = r sena e quella dal punto O(5) è r.
1) MOMENTO RISPETTO ALL'ASSE N-N
Per definizione J = m R2, nella quale R è la distanza dall'asse di rotazione, nel nostro caso y, e quindi:
dJ = dm y2 = (g h / g) r da dr r2 sen2a = (g h / g) r3 sen2a da dr
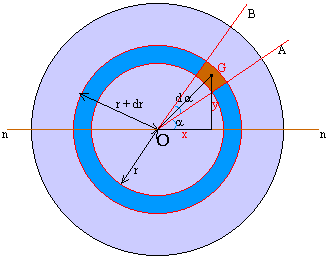
Per ottenere il momento d'inerzia totale dobbiamo integrare: l'angolo a varia fra 0 e 2p mentre r varia fra 0 e R. Otteniamo quindi
J = ò 0;2p ò 0;R (g h / g) r3 sen2a da dr = (g h / g) ò 0;2p sen2a da ò 0;R r3 dr
Questo è un integrale doppio di immediata soluzione: si separano le variabili e si integra congiuntamente(6):
Jn = (g h / g) (- sen2a / 4 + a / 2)0;2p (r4 / 4)0;R = (g h / g) (p - 0) (R4 / 4) = (g h / g) p R4 / 4 = (g h / g) p D4 / 64
Evidenziando la massa m = (g h / g) p R2 possiamo scrivere:
Jn = m R2 / 4
2) MOMENTO RISPETTO AL PUNTO O (MOMENTO DI INERZIA POLARE)
Per definizione J = m R2, nella quale R è la distanza dall'asse di rotazione, nel nostro caso r, e quindi:
dJ = dm r2 = (g h / g) r da dr r2 = (g h / g) r3 da dr
Per ottenere il momento d'inerzia totale dobbiamo integrare: l'angolo a varia fra 0 e 2p mentre r varia fra 0 e R. Otteniamo quindi
J = ò 0;2p ò 0;R (g h / g) r3 da dr = (g h / g) ò 0;2p da ò 0;R r3 dr
Questo è un integrale doppio di immediata soluzione: si separano le variabili e si integra congiuntamente:
Jp = (g h / g) (a)0;2p (r4 / 4)0;R = (g h / g) (2 p - 0) (R4 / 4) = (g h / g) p R4 / 2) = (g h / g) p D4 / 32
Evidenziando la massa m = (g h / g) p R2 possiamo scrivere:
Jn = m R2 / 2
C) MOMENTO DI INERZIA DI MASSA DI UN ANELLO
1) Utilizzando i risultati già ottenuti:
Poiché il momento d'inerzia è una funzione sommabile rispetto alla massa(7), per trovare il momento di inerzia Ja di un anello basta sottrarre da quello dell'anello considerato pieno Jp il momento Jv della parte vuota(8). Prendiamo il caso del momento rispetto ad un asse: diciamo Re il raggio del disco considerato pieno e Ri quello del vuoto. Avremo:
Ja = Jp - Jv = (g h / g) p Re4 / 4 - (g h / g) p Ri4 / 4 = (g h / 4 g) (Re4 - Ri4)
oppure, usando i diametri(9):
Ja = Jp - Jv = (g h / 64 g) (De4 - Di4)
2) Eseguendo il calcolo diretto:
Prendiamo il caso del momento rispetto ad un punto: l'equazione differenziale è la stessa ma r varia da Ri a Re e quindi:
Ja = (g h / g) (a)0;2p (r4 / 4)Ri;Re = (g h / g) (2 p - 0) (Re4 - Ri4) / 4) = (g h / g) p (Re4 - Ri4) / 2) = (g h / g) p (De4 - Di4) / 32
D) CONFRONTO FRA I DUE MOMENTI DI INERZIA
Confrontando il momento di inerzia di massa di un disco rispetto ad un asse e quello rispetto ad un punto si ha:
Jp / Jn = (g h / g) p D4 / 32 / (g h / g) p D4 / 64 = 2
E' questa una regola generale dei momenti di inerzia: il momento di inerzia rispetto ad un punto, detto polo, vale la somma di due momenti di inerzia calcolati rispetto a due assi ortogonali passanti per il polo, cioè, detti m-m e n-n due assi ortogonali passanti per il polo O, si ha (vedi figura):
JO = Jm + Jn
E) MOMENTO DI INERZIA DI UNA SUPERFICIE
Supponiamo di avere un solido di spessore h = 1 e di peso specifico g = 1. Allora, almeno in via intuitiva, la massa assume il significato di area A e il volume assume il significato di superficie, cioè
J = m R2 —> A R2 nella quale R è la distanza dall'asse di rotazione.
1) momento di inerzia di un cerchio:
a) rispetto ad un diametro: con riferimento alla figura del punto B) abbiamo:
dJ = dm y2 = dA y2 = r da dr r2 sen2a = r3 sen2a da dr
L'integrale di questa funzione è quello già calcolato e quindi:
Jn= (- sen2a / 4 + a / 2)0;2p (r4 / 4)0;R = (p - 0) (R4 / 4) = p R4 / 4 = p D4 / 64
b) rispetto al centro: richiamando quanto detto al punto a) e quanto detto al punto D) si ottiene subito:
Jp = p R4 / 2 = p D4 / 32
2) momento di inerzia di un rettangolo:
a) rispetto al lato b:
Con riferimento alla figura qui sotto: l'area della striscia infinitesima in verde è dA = b dh, la distanza dal lato inferiore è y e quindi il suo momento d'inerzia è:
dJ = dA y2 = b dy y2
con y variabile da 0 a h. Integrando si ottiene:
Jb = b ò 0;h y2 dy = b (y3 / 3)0;h = b h3 / 3
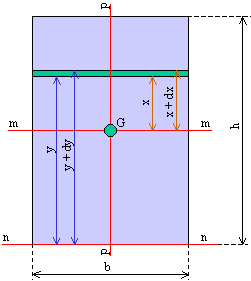
b) rispetto all'asse baricentrico m:
L'equazione differenziale è la stessa, sostituendo x al posto di y, ma il campo di integrazione è da - h / 2 a + h / 2: in successione si ottiene:
dJ = dA x2 = b dx x2
Jm = b ò -h/2;+h/2 x2 dx = b (x3 / 3)-h/2;+h/2 = b [(h / 2)3 - (- h / 2)3] / 3 = b (2 h3 / 8) / 3 = b h3 / 12
c) rispetto al baricentro: adoperiamo quanto si è detto al punto D). Un momento lo abbiamo già: è Jm; l'altro, Jp, lo otteniamo semplicemente scambiando fra loro b e h: Jp = h b3 / 12 e quindi:
JG = Jm + Jp = (bh3 + b3h) / 12 = (b h / 12) (h2 + b2)
F) TEOREMA DI TRASPOSIZIONE
Il momento di inerzia rispetto ad un asse qualunque è uguale alla somma di: a) momento di inerzia rispetto ad un asse parallelo ma baricentrico e b) il prodotto fra la massa concentrata nel baricentro e il quadrato della distanza fra i due assi. Con riferimento alla figura seguente si ha (in giallo l'area vuota):
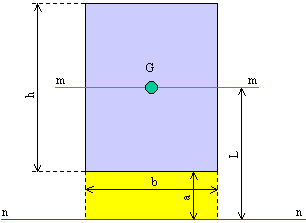
Jn = Jm + b h L2 = bh3 / 12 + b h (a + h / 2)2 = bh3 / 12 + b h (2 a + h)2 / 4
Per dimostrarlo adoperiamo i risultati raggiunti in C) e in E) 2) a).
Considerando il rettangolo costituito dalla parte viola e quella gialla il momento di inerzia è
Jn = b (h + a)3 / 3
Considerando solo il rettangolo giallo il momento di inerzia è:
Jn = b a3 / 3
Poiché il rettangolo giallo è in realtà vuoto, il momento d'inerzia è la differenza fra i due calcolati, cioè:
Jn = b (h + a)3 / 3 - b a3 / 3
Sviluppando il cubo del binomio e ordinando si ottiene:
Jn = b (h + a)3 / 3 - b a3 / 3 = b h3 / 3 + b a h2 + b a2 h + b a3 / 3 - b a3 / 3 = b h3 / 3 + a b h (a + h)
Riprendendo l'espressione scritta più su, sviluppando il quadrato e ordinando si ottiene
Jn = bh3 / 12 + b h (2 a + h)2 / 4 = b h3 / 12 + b h (4 a2 + 4 a h + h2) / 4 = b h3 / 3 + a b h (a + h)
cioè lo stesso risultato ottenuto in precedenza, come si doveva dimostrare.
G) MOMENTO DI INERZIA DI UNA SUPERFICIE QUALUNQUE
Avendo tempo e pazienza: si divide la superficie in strisce, preferibilmente di uguale ampiezza, in una scala opportuna, si determina la posizione del baricentro (vedi il paragrafo baricentro nel capitolo Meccanica) di ciascuna striscia e poi di ciascuna si calcola il momento di inerzia rispetto all'asse n-n dato usando la definizione:
Jni = mi ri2 Jn = S Jni = S mi ri2
Se si cerca il momento di inerzia polare rispetto al punto O si ripete il lavoro rispetto a due assi n-n e m-m perpendicolari fra loro e passanti per O. Dopo di ché i due momenti si sommano:
JO = Jn + Jm
Se la superficie è composta di figure semplici (triangoli, rettangoli, cerchi, ...) si usa la regola che dice che la funzione momento è sommabile: nei manuali si cercano i momenti delle singole figure e poi si sommano i risultati, usando anche il teorema di trasposizione.
H) ESEMPIO
Data la figura qui sotto determinare il momento di inerzia rispetto all'asse n-n:
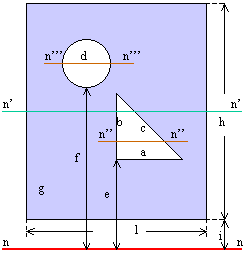
1) Momento di inerzia del triangolo e del cerchio rispetto agli assi n'' e n''' paralleli ad n passanti per il loro baricentro.
2) Uso del teorema di trasposizione rispetto all'asse n'.
3) Momento di inerzia del rettangolo considerato pieno rispetto all'asse n' parallelo e baricentrico.
4) Momento di inerzia del rettangolo con i fori rispetto all'asse n' parallelo e baricentrico: differenza con i due momenti precedenti.
5) Uso del teorema di trasposizione rispetto all'asse n.
(1) Se si conosce l'equazione l'integrazione si esegue con i metodi della matematica.
(2) Le due scale possono essere diverse: per esempio in topografia si usa una scala per le distanze orizzontali e un'altra (di solito 100 o 1.000 volte minore) per quelle verticali.
(3) Le unità di misura adoperate sono senza significato alcuno: sono servite soltanto per esemplificare.
(4) L'elemento è stato considerato come un parallelepipedo e inoltre non si è presa la larghezza media che è dlm = (r + dr / 2) da = r da + dr da / 2 = r da essendo dr da / 2 trascurabile rispetto all'altro addendo (attenzione: è trascurabile non zero).
(5) La distanza è r + dr / 2. Ma dr / 2 è trascurabile rispetto ad r e quindi resta r.
(6) L'integrale indefinito di sen2a da è: a / 2 - sen2a / 4 + C.
(7) Riprendiamo l'esempio fatto nella pagina precedente di un sasso legato ad una funicella: se leghiamo un sasso di massa doppia oppure due sassi uguali il momento di inerzia raddoppia. Ciò non vale per il raggio di rotazione: raddoppiando la distanza il momento quadruplica.
(8) Ciò equivale a dire che la parte vuota ha momento di inerzia negativo. In questo modo è possibile calcolare il momento di inerzia di solidi con buchi.
(9) Attenzione: PRIMA si calcolano le potenze e POI si esegue la differenza. Esempio: 54 - 34 = 625 - 81 = 544; (5 - 3)4 = 16.