Per esempio, consideriamo un campo scalare neutro ![]() ,
funzione dei punti dello spazio-tempo x, e sia:
,
funzione dei punti dello spazio-tempo x, e sia:
| (2.33) |
la densità di Lagrangiana, che dipende solo dal campo e dalle sue derivate prime. Sia I(M) l'integrale d'azione, definito per una regione arbitraria M dello spazio-tempo:
| (2.34) |
e imponiamo che, per una variazione del campo che si annulli sul contorno di M, l'azione abbia un valore stazionario. Come è noto, tale condizione conduce alle equazioni di Euler-Lagrange:
| |
(2.35) |
che rappresentano le equazioni del moto per i campi.
Per quantizzare il sistema classico, descritto dalle (2.35),
usando il formalismo canonico della meccanica quantistica non relativistica,
è necessario introdurre variabili coniugate. Pertanto ad un istante
fissato tsuddividiamo lo spazio in un reticolo di cellette uguali
di volume ![]() .
Approssimiamo il valore del campo nella cella con il suo valor medio all'interno
della cella stessa; il sistema è quindi descritto dall'insieme discreto
di coordinate generalizzate:
.
Approssimiamo il valore del campo nella cella con il suo valor medio all'interno
della cella stessa; il sistema è quindi descritto dall'insieme discreto
di coordinate generalizzate:
| (2.36) |
dove l'integrazione è sulla ima cella di dimensione ![]() .
.
Su questo reticolo discreto, le derivate spaziali dei campi devono essere sostituite dalle differenze dei valori dei campi in due celle contigue; la Lagrangiana è perciò data da:
| (2.37) |
dove ![]() è la media della derivata temporale di
è la media della derivata temporale di ![]() sulla ima cella, e
sulla ima cella, e ![]() è il valor medio del campo nella cella contigua.
è il valor medio del campo nella cella contigua.
Gli impulsi coniugati alle ![]() sono:
sono:
| (2.38) |
L'Hamiltoniana del sistema discreto è allora data da:
| H | = | ||
| = | |||
| = | (2.39) |
Al limite per ![]() ,
il campo coniugato a
,
il campo coniugato a ![]() è
definito da:
è
definito da:
| |
(2.40) |
La Lagrangiana e l'Hamiltoniana diventano:
| L(t) | = | 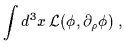 |
(2.41) |
| H | = | 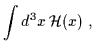 |
(2.42) |
dove le integrazioni sono estese a tutto lo spazio per t fissato,
e la densità di Hamiltoniana ![]() è definita da:
è definita da:
| |
(2.43) |
Si può quindi approssimare la teoria interpretando le coordinate e gli impulsi coniugati della approssimazione discreta, come operatori di Heisenberg, e sottoponendoli alle usuali regole di commutazione a tempi uguali che, nel limite al continuo, assumono la forma:
| |
(2.44) |
Con queste prescrizioni è possibile estendere al formalismo della teoria dei campi la formula (2.21) ottenuta nel paragrafo precedente, che esprime l'operatore di evoluzione temporale in termini dell'integrale di cammino [13]:
![$\displaystyle \frac{\epsilon^3}{2\pi\hbar}\int e^{\frac{i}{\hbar}\epsilon^3\left[\pi_N(\phi_N-\phi_{N-1}) -{\cal H}(\pi_N,\phi_{N-1})\Delta t \right]}d\pi_N$](img127.gif) |
|||
![$\displaystyle \frac{\epsilon^3}{2\pi\hbar}\int e^{\frac{i}{\hbar}\epsilon^3\le......hi_{N-1}-\phi_{N-2})-{\cal H}(\pi_{N-1},\phi_{N-2})\Delta t \right]}d\pi_{N-1}$](img128.gif) |
|||
![$\displaystyle \frac{\epsilon^3}{2\pi\hbar}\int e^{\frac{i}{\hbar}\epsilon^3\left[\pi_1(\phi_1-\phi_0)-{\cal H}(\pi_1,\phi_0)\Delta t \right]}d\pi_1 \; .$](img129.gif) |
(2.45) | ||
Nel limite al continuo, questa espressione diventa:
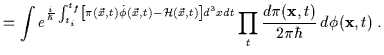 |
(2.46) | ||
Se, in particolare, si considera un sistema in cui la densità di Hamiltoniana sia quadratica negli impulsi coniugati, come, ad esempio, nel caso di un campo scalare neutro descritto dalla densità di Lagrangiana:
| (2.47) |
si può considerare la separazione nelle variabili ![]() e
e ![]() ,
e l'elemento di matrice dell'operatore di evoluzione temporale diventa:
,
e l'elemento di matrice dell'operatore di evoluzione temporale diventa:
| = | |||
| = | 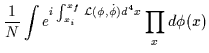 |
||
| = | ![$\displaystyle \int {\cal D}[\phi (x)] \, e^{iI[\phi (x)]} \; .$](img136.gif) |
(2.48) |
In teoria dei campi, tutte le quantità fisiche, e in particolare
i propagatori di Feynman, sono derivabili dalla ampiezza di transizione
da vuoto a vuoto in presenza di sorgenti esterne ![]() [14]. Questa ampiezza, che indichiamo con
W[J], può essere calcolata tramite la (2.48)
aggiungendo alla Lagrangiana un termine:
[14]. Questa ampiezza, che indichiamo con
W[J], può essere calcolata tramite la (2.48)
aggiungendo alla Lagrangiana un termine:
| (2.49) |
nel limite ![]() e
e ![]() ;
riconsiderando l'espressione generale:
;
riconsiderando l'espressione generale:
| (2.50) |
Il funzionale W[J] è in generale un integrale oscillatorio e mal definito anche nell'approssimazione discreta del reticolo. Esistono due modi per risolvere questo problema: