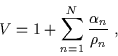6.6.1  Equilibrio statico nel limite classico

Per la soluzione multipla di buchi neri dilatonici massimamente carichi, possiamo scegliere per V una espressione del tipo:

$$V = 1 + \sum_{n=1}^{N} \frac{\alpha_n}{\rho_n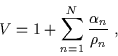} \; ,$$ (6.55)

 

che dà una metrica di Bertotti-Robinson in prossimità di ciascuno degli N orizzonti, ed è asintoticamente piatta all'infinito.

Nell'analizzare la condizione di equilibrio statico, bisogna osservare che il sistema in esame è governato da tre tipi di forze: l'attrazione gravitazionale, la repulsione magnetica e la forza scalare attrattiva mediata dal dilatone $\phi$.

Per definire i valori delle masse, delle cariche magnetiche e delle cariche scalari, consideriamo il limite classico a bassa energia delle soluzioni (6.46) - (6.48).

Per il calcolo delle masse M_i osserviamo che le componenti spaziali della metrica canonica:

$$\left( 1 + \sum_{n=1}^N \frac{\alpha_n}{\rho_n}\right)^{\frac{3+k}{2}} \delta_{ij}$$ g_ij =

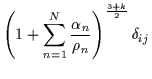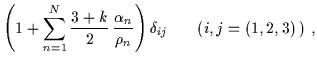$$\stackrel{\rho \to \infty}{\simeq} \left( 1 + \sum_{n=1}^N \frac{3+k}{2} \, \frac{\alpha_n}{\rho_n}\right) \delta_{ij}\;\;\;\;\;\; \left(i,j=(1,2,3) \, \right) \; ,$$ (6.56)

 

nel limite asintotico per $\rho \to \infty$ devono tendere al limite node0.oniano:

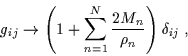$$g_{ij} \to \left( 1 + \sum_{n=1}^N\frac{2 M_n}{\rho_n} \right) \delta_{ij} \; ,$$ (6.57)

 

dove M_n è la massa dell'n^mo buco nero. Segue che le soluzioni asintoticamente piatte descrivono una distribuzione di buchi neri estremi con masse:

$$M_n = \frac{3+k}{4} \, \alpha_n \; .$$ (6.58)

 

Analogamente, le componenti spaziali del tensore di campo elettromagnetico:

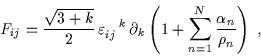$$F_{ij} = \frac{\sqrt{3+k}}{2}\,\varepsilon_{ij}^{\;\;\:\:k} \......k\left( 1 + \sum_{n=1}^N\frac{\alpha_n}{\rho_n}\right) \; ,$$ (6.59)

 

tendono al limite classico:

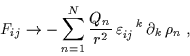$$F_{ij} \to - \sum_{n=1}^N \frac{Q_n}{r^2} \,\varepsilon_{ij}^{\;\;\:\:k} \,\partial_k \, \rho_n \; ,$$ (6.60)

 

dove Q_n è la carica magnetica dell'n^mo buco nero. Si ha perciò:

$$Q_n = \frac{\sqrt{3+k}}{2} \, \alpha_n \; .$$ (6.61)

 

Infine si possono definire le cariche scalari $\Sigma_n$dal comportamento asintotico del dilatone:

$$\phi \frac{1}{4} \sqrt{(1-k)(3+k)} \,\ln \left( 1 + \sum_{n=1}^{N} \frac{\alpha_n}{\rho_n} \right)$$ =

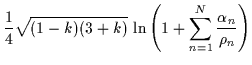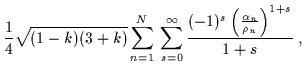$$\stackrel{\rho \to \infty}{\simeq} \frac{1}{4} \sqrt{(1-k)(3+k)}\sum_{n=1}^N \: \sum_{s=0}^{\infty}\frac{(-1)^s \left( \frac{\alpha_n}{\rho_n}\right)^{1+s}}{1+s} \; ,$$ (6.62)

 

che, nel limite per $\rho \to \infty$ deve ridursi a:

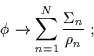$$\phi \to \sum_{n=1}^N \frac{\Sigma_n}{\rho_n} \; ;$$ (6.63)

 

si ha dunque:

$$\Sigma_n = \frac{1}{4} \sqrt{(1-k)(3+k)} \, \alpha_n \; .$$ (6.64)

 

La condizione di equilibrio statico tra gli N buchi neri estremi sarà allora espressa dal bilanciamento della forza attrattiva di Newton:

$$F_N = \frac{M_i M_j}{\rho^2} =\frac{3+k}{16}\, \frac{\alpha_i \alpha_j}{\rho^2} \; ,$$ (6.65)

 

della forza repulsiva di Coulomb:

$$F_Q = \frac{q_i q_j}{\rho^2} =\frac{3+k}{4}\, \frac{\alpha_i \alpha_j}{\rho^2} \; ,$$ (6.66)

 

e della forza scalare dilatonica attrattiva:

$$F_D = \frac{\Sigma_i \Sigma_j}{\rho^2} =\frac{(1-k)(3+k)}{16}\, \frac{\alpha_i \alpha_j}{\rho^2} \; ;$$ (6.67)

 

deve cioè essere:

$$F_{tot} = F_N - F_Q + F_D = 0 \; .$$ (6.68)

 

Una semplice sostituzione algebrica mostra allora che tale condizione è identicamente soddisfatta per tutti i valori di k, e rappresenta una generalizzazione al caso dilatonico della soluzione di Majumdar-Papapetrou della relatività generale.

 
1999-03-18