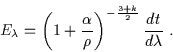6.6  La metrica ``canonica''

Nel capitolo precedente abbiamo descritto la soluzione di buchi neri multipli nell'usuale sistema di Einstein-Maxwell, nota come soluzione di Majumdar-Papapetrou, che rappresenta l'equilibrio statico tra buchi neri estremi di Reissner-Nordström, in cui l'attrazione gravitazionale e la repulsione elettrostatica si bilanciano esattamente. Recentemente [40] è stata studiata la soluzione di buchi neri multipli nella teoria delle corde in un sistema di Einstein-Maxwell modificato dalla presenza di un campo scalare dilatonico, accoppiato in modo non minimale (k = -1) al campo di Maxwell F, dove la condizione di equilibrio deve tener conto anche della forza scalare.

È perciò interessante considerare l'interpolazione tra questi due casi estremi. Tale studio è stato discusso da Shiraishi [42] nel caso multidimensionale, a partire da una azione modificata dilatonica, che è correlata all'azione delle corde (6.8) da noi considerata dalla trasformazione conforme della metrica:

$$\hat{g}_{\mu \nu} = e^{-2\phi} g_{\mu \nu} \; .$$ (6.43)

 

In termini della metrica ``canonica'', l'azione assume la forma:

$$I = \frac{1}{16\pi} \int d^4x \sqrt{-\hat{g}}\,\left[ \hat{......\nabla}\hat{\phi})- e^{-2a\hat{\phi}}\hat{F}^2 \right] \; ,$$ (6.44)

 

dove:

$$a\hat{\phi} = \phi \;\;\;\;\; ; \;\;\;\;\;a\hat{F} = F$$   $$a = \sqrt{\frac{1-k}{3+k}} \; .$$  

Le equazioni di campo relative a questa azione sono (omettendo per brevità il simbolo `` $\hat{\rule{0mm}{2mm}\;\;\rule{0mm}{2mm}}$''):

$$\nabla_{\mu} \left(e^{-2a\phi}F_{\mu \nu} \right) = 0$$ (a)

$$\nabla^2 \phi + \frac{1}{2} \, a \, e^{-2a\phi} F^2 = 0$$ (b)

$$R_{\mu \nu} = 2 \,\nabla_{\mu}\phi \nabla_{\nu}\phi+ 2 \,e^{-2a\phi}F_{\mu \rho} F_{\nu}^{\;\:\rho}-\frac{1}{2} \,g_{\mu \nu} e^{-2a\phi}F^2 \; .$$ (c) (6.45)

 

Una soluzione per queste equazioni di campo, nel caso di buchi neri magnetici estremi multipli, è data da:

   

$$- V^{-\frac{3+k}{2}} dt^2 + V^{\frac{3+k}{2}}d\mbox{\bf x} \cdot d\mbox{\bf x}$$         ds² = (6.46)

$$e^{-2a\phi} V^{\frac{-1+k}{2}}$$ = (6.47)

$$\frac{\sqrt{3+k}}{2} \,\varepsilon_{ij}^{\;\;\:\:k} \,\partial_k V \; ,$$ F_ij = 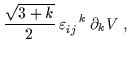(6.48)

 

che si ottiene applicando la trasformazione conforme (6.43) alle soluzioni ottenute prima per le equazioni di campo relative all'azione (6.8).

V è una funzione che deve, come prima, soddisfare la condizione:

$$\mbox{\boldmath$\nabla$ }^2 V = 0 \; .$$  

Nel caso di un singolo buco nero estremo si può ancora considerare una espressione del tipo:

$$V = 1 + \frac{\alpha}{\rho} \; ;$$ (6.49)

 

tuttavia lo scalare di curvatura relativo a questa metrica è:

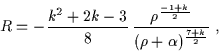$$R = - \frac{k^2+2k-3}{8} \,\frac{\rho^{\frac{-1+k}{2}}}{(\rho + \alpha)^{\frac{7+k}{2}}} \; ,$$ (6.50)

 

e, in prossimità di $\rho = 0$:

$$\lim_{\rho \to 0} R =\left\{\begin{array}{lc}\to \infty &......< 1) \\ [.3 cm]0 & \;\;\;\;\; (k=1) \; .\end{array}\right.$$ (6.51)

 

Perciò, nell'intervallo $-1 \le k < 1$, la superficie $\rho = 0$rappresenta una vera singolarità di curvatura, non schermata da alcun orizzonte , e quindi non ritenuta fisicamente accettabile secondo la già accennata ipotesi di Penrose.

Tuttavia, nel limite k=1, si riottiene il caso di Reissner-Nordström estremo, in cui la superficie $\rho = 0$ non presenta alcuna singolarità.

Lo studio delle geodetiche radiali mostra alcuni aspetti peculiari della metrica ``canonica''; infatti le geodetiche ``space-like'' si mantengono finite per tutti i valori di k (eccetto, naturalmente, nel caso già discusso k = 1):

$$\int_{l(\rho_0)}^{l(0)} dl \int_{\rho_0}^{0} d\rho \left(1+\frac{\alpha}{\rho}\right)^{\frac{3+k}{4}}$$ =

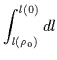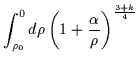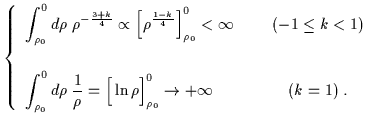$$\stackrel{\rho \to 0}{\simeq} \left\{\begin{array}{lc}\displaystyle\int_{\rho_0}^{0} d\rho \......_{\rho_0}^0\to + \infty& \;\;\;\;\; (k = 1) \; .\end{array}\right.\nonumber$$ (6.52)

 

Inoltre, relativamente alla stessa distanza,per tutti i valori di k, si mantengono finite le geodetiche ``time-like'':

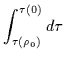$$\int_{\tau(\rho_0)}^{\tau(0)} d\tau \int_{\rho_0}^{0} d\rho\left[-\left(1+\frac{\alpha}{\rho}\right)^{-\frac{3+k}{2}}+ E_{\tau}^2 \right]^{-1/2}$$ =

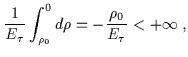$$\stackrel{\rho \to 0}{\simeq} \frac{1}{E_{\tau}}\int_{\rho_0}^{0} d\rho= - \frac{\rho_0}{E_{\tau}}< +\infty \; ,$$ (6.53)

 

e ``light-like'':

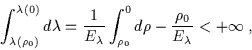$$\int_{\lambda(\rho_0)}^{\lambda(0)} d\lambda =\frac{1}{E_{\......rho_0}^{0} d\rho- \frac{\rho_0}{E_{\lambda}}< +\infty \; ,$$ (6.54)

 

dove:

$$E_{\lambda} = \left( 1 + \frac{\alpha}{\rho} \right)^{-\frac{3+k}{2}}\frac{dt}{d\lambda} \; .$$  
 

 
1999-03-18