|
|
|
|
|
|
|
|
|
|
L'espressione generale della trasmissione di calore attraverso un muro composito si può scrivere:
nella quale Q è il calore che attraversa il muro, k il coefficiente di trasmissione globale, S l'area della superficie di trasmissione e Dt è la differenza di temperatura fra le due facce della parete.
Moltiplicando il valore di k per l'area S della superficie interessata alla trasmissione si ottiene il valore di K (Cal / h °C) e quindi infine:
Questa espressione è del tutto simile (non uguale!) a quella adoperata in elettrotecnica con il nome di legge di Ohm.
Riprendiamo il problema del paragrafo precedente e calcoliamo i valori delle temperature strato per strato per tracciarne il diagramma all'interno del muro. Per determinare la portata di calore supponiamo che per mantenere la temperatura costante di t1 = 600 °C si bruci gasolio con portata di q = 250 kg / h con un rendimento(*) di h = 86 %. Il potere calorifico inferiore del gasolio sia p.c.i. = 9.500 Cal / kg e quindi:
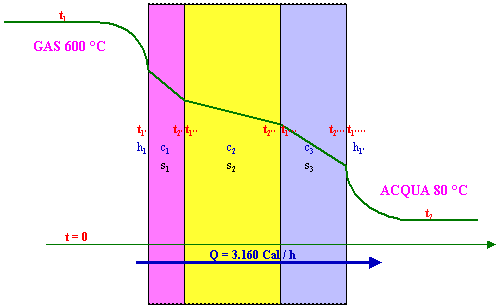
Supponiamo, come si è detto al paragrafo precedente, che:
1) A sinistra ci sia un gas alla temperatura costante t1 = 600 °C e che a destra ci sia acqua alla temperatura costante t2 = 80 °C.
2) Il muro è costituito da uno strato di spessore s1 = 10 mm di acciaio, uno strato di spessore s2 = 30 cm di lana di roccia, uno strato di spessore
s3 = 12 cm di mattone refrattario.
3) Il coefficiente di convezione gas - acciaio sia h1 = 50 Cal / h m2 °C e il coefficiente di convezione mattone - acqua sia h2 = 48,7 Cal / h m2 °C.
4) Il coefficiente di conduzione interno dell'acciaio con 5 % di nichel sia c1 = 25 Cal / h m °C; della lana di roccia sia c2 = 0,047 Cal / h m °C; del mattone refrattario sia c3 = 0,6 Cal / h m °C(*).
5) L'area della superficie di trasmissione sia S = 40 m2.
Con queste ipotesi la portata di calore che attraversa il muro, utilizzando il valore di k calcolato al paragrafo precedente, è:
Ricordando che la quantità di calore Q che arriva nell'acqua è la stessa che entra nel muro e attraversa i diversi strati, possiamo calcolare i diversi salti di temperatura, usando le espressioni:
nelle quali h si riferisce alla convezione e c / s alla conduzione. Da queste si ricava in successione:
Q = c S D''t /s Q = c S (t1' - t2') / s t1' - t2' = Q s / c S = 3.140x0,010 / 25x40 = 0,03 °C
t2' = t1' - 0,03 = 598,4 - 0,03 = 598,37 °C
t1'' - t2'' = Q s / c S = 3.140x0,30 / 0,047x40 = 501,1 °C t2'' = t1'' - 501,1 = t2' - 501,1 = 598,37 - 501,1 = 97,31 °C
t1''' - t2''' = Q s / c S = 3.140x0,12 / 0,6x40 = 15,7 °C t2''' = t1''' - 15,7 = t2'' - 15,7 = 97,31 - 15,7 = 81,61 °C
t1'''' - t2 = Q / h S = 3.140 / 48,7x40 = 1,61 °C t2 = t1'''' - 1,61 = 81,61 - 1,61 = 80 °C
OSSERVAZIONI
A) La composizione e la disposizione degli strati non sono certo le più indicate per raggiungere un comprensibile obiettivo impiantistico. Molto meglio sarebbe stato invertire fra loro lo strato di acciaio e quello di mattone refrattario.
B) Come era ovvio non c'è quasi caduta di temperatura né fra gas e acciaio né all'interno dell'acciaio: i coefficienti di convezione e di conduzione sono grandi e quindi il calore "passa" molto facilmente.
C) Come era ovvio la gran caduta di temperatura avviene nell'isolante che risulta molto efficace.
D) Come si è detto al paragrafo precedente, il coefficiente di convezione mattone - acqua h2 = 48,7 Cal / h m2 °C è stato "aggiustato" per far tornare i conti. In realtà bisogna ricordare che tutti i coefficienti variano al variare della temperatura, cioè sono funzioni di t, per cui occorrerebbe fare un lavoro di approssimazione continua, rivedendo continuamente i loro valori man mano che si stabiliscono le diverse temperature. Nel nostro caso il valore di k dipende quasi esclusivamente dalla lana di roccia, ma poi i diversi salti di temperatura dipendono dai valori di h e di c.
Per esempio se ponessimo il coefficiente di convezione gas - acciaio h1 = 5 Cal / h m2 °C, il valore di k diventerebbe k = 0,147 (poco diverso da 0,151), ma allora sarebbe t1' = 15,7 °C, invece di 1,6 °C.
(*) Il resto del calore viene disperso nei fumi.