|
|
 |
Isomorfismi tra gruppi |
 |
|
|
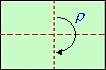
Ricordate il gruppo delle
isometrie piane del rettangolo ? |
Avevamo indicato con r la rotazione in senso orario di p
attorno al centro del rettangolo, con th la riflessione rispetto all'asse di simmetria orizzontale e con tv la
riflessione rispetto all'asse di simmetria verticale: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
tv |
|
B |
|
|
|
|
|
 |
|
|
|
th |
|
|
|
D |
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Il gruppo delle isometrie di
un rettangolo è l'insieme |
G ={id, r, th, tv}
|
con
seguente tavola di moltiplicazione: |
|
° |
id |
r |
th |
tv |
|
|
id |
id |
r |
th |
tv |
|
|
r |
r |
id |
tv |
th |
|
|
th |
th |
tv |
id |
r |
|
|
tv |
tv |
th |
r |
id |
|
|
|
|
|
|
|
|
|
Che noia i rettangoli,
molto meglio una bella scacchiera quadrata: |
|
|
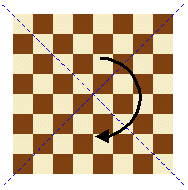
Quante sono le isometrie di
una scacchiera quadrata? La presenza di due colori diversi ci fa intuire che saranno
sicuramente in numero inferiore rispetto a quelle di un quadrato e in effetti è immediato
verificare che sono solo quattro: l'identità id, la rotazione r di p radianti in senso orario
attorno al centro della scacchiera, le riflessioni tAe tB rispetto alle due diagonali: |
| A |
|
|
|
|
|
|
|
|
B |
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| D |
|
|
|
|
|
|
|
|
C |
|
La tavola di moltiplicazione
si ricava immediatamente e si trova che il gruppo delle isometrie di una scacchiera è
l'insieme |
G' = {id, r,
tA, tB} |
con
seguente tavola di moltiplicazione: |
|
° |
id |
r |
tA |
tB |
|
|
id |
id |
s |
tA |
tB |
|
|
r |
r |
id |
tB |
tA |
|
|
tA |
tA |
tB |
id |
r |
|
|
tB |
tB |
tA |
r |
id |
|
|
|
|
|
|
|
|
|
Affianchiamo le tavole
moltiplicative delle isometrie del rettangolo e della scacchiera |
|
° |
id |
r |
th |
tv |
|
|
° |
id |
r |
tA |
tB |
|
id |
id |
r |
th |
tv |
|
|
id |
id |
r |
tA |
tB |
|
r |
r |
id |
tv |
th |
|
|
r |
r |
id |
tB |
tA |
|
th |
th |
tv |
id |
r |
|
|
tA |
tA |
tB |
id |
r |
|
tv |
tv |
th |
r |
id |
|
|
tB |
tB |
tA |
r |
id |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e intuiamo che questi due
gruppi non sono poi così diversi. Tanto per cominciare, i due gruppi hanno entrambi
quattro elementi e poi sembra che il prodotto tra elementi avvenga nello stesso modo, è
come se quello che cambia siano i nomi di alcuni elementi , altrimenti le due tavole
sarebbero indistinguibili. Per tradurre nel linguaggio della matematica questa intuizione,
definiamo la funzione |
| j
: |
G |
® |
G' |
|
id |
® |
id |
|
r |
® |
r |
|
th |
® |
tA |
|
tv |
® |
tB |
|
e, a
partire dalla tavola delle isometrie del rettangolo, costruiamo una nuova tavola
sostituendo ogni elemento con la sua immagine tramite j |
|
° |
id |
r |
th |
tv |
|
|
° |
j(id) |
j(r) |
j(th) |
j(tv) |
|
|
|
° |
id |
r |
tA |
tB |
|
id |
id |
r |
th |
tv |
|
j |
j(id) |
j(id) |
j(r) |
j(th) |
j(tv) |
|
|
|
id |
id |
r |
tA |
tB |
|
r |
r |
id |
tv |
th |
|
 |
j(r) |
j(r) |
j(id) |
j(tv) |
j(th) |
|
= |
|
r |
r |
id |
tB |
tA |
|
th |
th |
tv |
id |
r |
|
|
j(th) |
j(th) |
j(tv) |
j(id) |
j(r) |
|
|
|
tA |
tA |
tB |
id |
r |
|
tv |
tv |
th |
r |
id |
|
|
j(tv) |
j(tv) |
j(th) |
j(r) |
j(id) |
|
|
|
tB |
tB |
tA |
r |
id |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
La tavola
così ottenuta è proprio quella delle isometrie della scacchiera. Come si traduce il
fatto che le due tavole sembravano definire la stessa operazione se si astraeva dai nomi
degli elementi? Intendevamo dire che j(a°b) = j(a)°j(b)
"a,bÎG, ad esempio j(th)°j(r) = j(tv)
= j(th°r) |
I due
gruppi quindi non sembrano molto diversi. |
Qualcuno potrebbe obiettare
che la cosa non è poi così sorprendente, infatti si tratta in entrambi i casi di gruppi
di isometrie di una figura piana e l'operazione di entrambi i gruppi è la composizione di
isometrie. |
Facciamo
un altro esempio. Una isometria del rettangolo determina, come noto, una
permutazione dei vertici |
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
A |
|
tv |
|
B |
|
|
|
|
|
 |
|
|
|
th |
|
|
|
D |
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
isometria |
|
permutazione
dei vertici |
|
id |
|
id |
|
r |
|
(A C)(B D) |
|
th |
|
(A D)(B C) |
|
tv |
|
(A B)(C D) |
|
Ebbene
l'insieme G'' = {id,
(A C)(B D), (A D)(B C),(A B)(C D)} è un gruppo
rispetto al prodotto di permutazioni ed ha la seguente tavola moltiplicativa: |
|
° |
id |
(A C)(B D) |
(A D)(B C) |
(A B)(C D) |
|
|
id |
id |
(A C)(B D) |
(A D)(B C) |
(A B)(C D) |
|
|
(A C)(B D) |
(A C)(B D) |
id |
(A
B)(C D) |
(A
D)(B C) |
|
|
(A D)(B C) |
(A D)(B C) |
(A
B)(C D) |
id |
(A
C)(B D) |
|
|
(A B)(C D) |
(A B)(C D) |
(A
D)(B C) |
(A
C)(B D) |
id |
|
|
|
|
|
|
|
|
|
Se definiamo la funzione
(usiamo ancora il simbolo j per
semplicità) |
| j
: |
G |
® |
G'' |
|
id |
® |
id |
|
r |
® |
(A C)(B D) |
|
th |
® |
(A D)(B C) |
|
tv |
® |
(A B)(C D) |
|
è
evidente come si passi tramite j dalla tavola moltiplicativa di G alla tavola
moltiplicativa di G'' : |
| ° |
id |
r |
th |
tv |
|
|
° |
id |
(A C)(B D) |
(A D)(B C) |
(A B)(C D) |
| id |
id |
r |
th |
tv |
|
j |
id |
id |
(A C)(B D) |
(A D)(B C) |
(A B)(C D) |
| r |
r |
id |
tv |
th |
|
 |
(A C)(B D) |
(A C)(B D) |
id |
(A
B)(C D) |
(A
D)(B C) |
| th |
th |
tv |
id |
r |
|
|
(A D)(B C) |
(A D)(B C) |
(A
B)(C D) |
id |
(A
C)(B D) |
| tv |
tv |
th |
r |
id |
|
|
(A B)(C D) |
(A B)(C D) |
(A
D)(B C) |
(A
C)(B D) |
id |
|
|
|
|
|
|
|
|
|
|
|
|
|
Ancora una volta, a parte il nome degli elementi, si tratta della stessa tavola, dato chej(a°b) = j(a)°j(b) "a,bÎG. Notiamo anche che l'operazione, anche se indicata con
lo stesso simbolo, è diversa: in j(a°b),
° indica
l'operazione di G mentre in j(a)°j(b) indica
l'operazione di G'' |
Qualche miscredente potrebbe
ancora obiettare che anche stavolta c'era da aspettarselo. Le operazioni dei due gruppi
sono sì diverse: in un caso composizione di isometrie e nell'altro di permutazioni, ma
abbiamo ottenuto le permutazioni dei vertici a partire dalle isometrie del rettangolo e
quindi questa somiglianza tra le tavole moltiplicative non sorprende e non si capisce
quindi perchè dovrebbe essere matematicamente rilevante. |
Abbandoniamo le isometrie e
consideriamo questa volta l' insieme numerico G''' ={1, 3, 5, 7} e come operazione binaria la moltiplicazione
modulo 8. Si dimostra immediatamente che questo insieme è un gruppo con la seguente
tavola moltiplicativa: |
|
|
* |
1 |
3 |
5 |
7 |
|
|
1 |
1 |
3 |
5 |
7 |
|
|
3 |
3 |
1 |
7 |
5 |
|
|
5 |
5 |
7 |
1 |
3 |
|
|
7 |
7 |
5 |
3 |
1 |
|
|
|
|
|
|
|
|
|
Affianchiamo le tavole
moltiplicative di G e G''' e noteremo subito che
si somigliano: |
|
° |
id |
r |
th |
tv |
|
|
* |
1 |
3 |
5 |
7 |
|
id |
id |
r |
th |
tv |
|
|
1 |
1 |
3 |
5 |
7 |
|
r |
r |
id |
tv |
th |
|
|
3 |
3 |
1 |
7 |
5 |
|
th |
th |
tv |
id |
r |
|
|
5 |
5 |
7 |
1 |
3 |
|
tv |
tv |
th |
r |
id |
|
|
7 |
7 |
5 |
3 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Se definiamo la funzione |
| j
: |
G |
® |
G''' |
|
id |
® |
1 |
|
r |
® |
3 |
|
th |
® |
5 |
|
tv |
® |
7 |
|
è
evidente come si passi tramite j dalla tavola moltiplicativa di G alla tavola
moltiplicativa di G''': |
|
° |
id |
r |
th |
tv |
|
|
* |
j(id) |
j(r) |
j(th) |
j(tv) |
|
|
|
* |
1 |
3 |
5 |
7 |
|
id |
id |
r |
th |
tv |
|
j |
j(id) |
j(id) |
j(r) |
j(th) |
j(tv) |
|
|
|
1 |
1 |
3 |
5 |
7 |
|
r |
r |
id |
tv |
th |
|
 |
j(r) |
j(r) |
j(id) |
j(tv) |
j(th) |
|
= |
|
3 |
3 |
1 |
7 |
5 |
|
th |
th |
tv |
id |
r |
|
|
j(th) |
j(th) |
j(tv) |
j(id) |
j(r) |
|
|
|
5 |
5 |
7 |
1 |
3 |
|
tv |
tv |
th |
r |
id |
|
|
j(tv) |
j(tv) |
j(th) |
j(r) |
j(id) |
|
|
|
7 |
7 |
5 |
3 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Notiamo che j(a°b)
= j(a)*j(b) "a,bÎG e quindi ancora una volta, a parte
il nome degli elementi e dell'operazione, si tratta in sostanza della stessa tavola
moltiplicativa. |
Questa volta anche il più
incallito tra gli scettici dovrà ammettere di essere rimasto sorpreso: due insiemi con
elementi di natura completamente diversa, due operazioni binarie di natura completamente
diversa eppure, se astraiamo dalla natura degli elementi e dalla natura
dell'operazione, ci verrebbe voglia di dire che i gruppi G
e G''' sono "uguali",
dato che hanno lo stesso numero di elementi e il modo in cui questi elementi vengono
moltiplicati è lo stesso. Certo però che la parola "uguali" ci sembra un pò
troppo impegnativa e inoltre noi abbiamo fatto solamente esempi di gruppi finiti. E se
avessimo gruppi con infiniti elementi? Non posso più dire che sono "uguali" se
hanno lo stesso "numero" di elementi e ... Però che cos'era la funzione j degli esempi se non una
biiezione? Invece di dire che gli insiemi sostegno hanno lo stesso numero di elementi,
posso dire che hanno la stessa potenza. |
| Vediamo se anche nel caso di gruppi infiniti
possiamo ... |
Consideriamo i gruppi (R,
+) e (R +, ·)
, dove con R + indichiamo i reali strettamente
positivi. Insiemi sostegno diversi e operazioni diverse, certo sembrerebbe difficile
trovare somiglianze tra questi due gruppi, ma i matematici non si arrendono mai. Per
iniziare, ricordiamo che un insieme infinito può essere messo in corrispondenza
biunivoca con una sua parte propria e, nel nostro caso, una biiezione è ad
esempio |
|
|
Che si tratta di una
biiezione si dimostra facilmente ... |
Risulta poi j(x+y) = 2x+y = 2x·2 y = j(x)·j(y) "x, yÎR |
Gli esempi visti giustificano
la seguente definizione: |
Definizione |
Siano dati due gruppi
(G, °) e (G',
à). Una funzione : G®G' si dice isomorfismo se |
|
|
|
|
Se esiste un
isomorfismo j : G®G'
, si dice che G è isomorfo a G' e
si scrive G ~ G' |
|
Proposizione |
L'isomorfismo è una
relazione di equivalenza tra gruppi |
Dim. |
La funzione identica su G, idG : G®G
definita da idG(a)
= a "aÎG, è un isomorfismo: |
che sia
biiettiva è ovvio e inoltre idG(a°b) = a°b = idG(a)°idG(b)
"a,bÎG |
Abbiamo
quindi dimostrato che G ~ G |
Consideriamo
un terzo gruppo (G'', ƒ). Se G
~ G' e G'
~ G'' , allora esistono un
isomorfismo j : G®G' e un isomorfismo y : G'®G''. |
Essendo
j e y
biiettive, il prodotto operatorio y
°j è una funzione biiettiva e inoltre |
y(j(a°b)) = y(j(a)àf(b)) = y(j(a))ƒy(j(b)) = y(j(a))ƒy(j(b)) "a,bÎG |
Il
prodotto operatorio y °f
: G®G'' è dunque
un isomorfismo e quindi G ~ G'' |
Resta
da dimostrare che se G ~ G',
allora G' ~ G |
Se G
~ G', allora esiste un
isomorfismo j : G®G' . Essendo j biiettiva esiste la funzione inversa j -1 : G'®G , anch'essa biiettiva. Devo far vedere che |
j -1(a' à b' ) = j -1(a' ) ° j -1(b' ) "a',b'ÎG' |
Si può
fare in due modi: sfruttando il fatto che j è
iniettiva oppure che j è suriettiva: |
j(j
-1(a' à b' )) = a' à b' "a',b'ÎG' |
| j(j -1(a' ) ° j -1(b' )) = j(j -1(a' )) à j(j -1(b' )) = a' à b'
"a',b'ÎG' |
Essendo
j iniettiva, j( j
-1(a' à b' )) = j( j -1(a' ) i j -1(b' ))  j -1(a' à b' ) = j
-1(a' ) ° j -1(b' ) j -1(a' à b' ) = j
-1(a' ) ° j -1(b' ) |
Essendo
j suriettiva, $a,bÎG: a' = j(a) e b' = j(b) e quindi |
j -1(a' à b' ) = j -1(j(a) à f(b)
) =j -1(j(a°b) ) = a°b |
| j
-1(a' )
°
j -1(b' ) = j -1(j(a) ) ° j -1(j(a) ) = a°b |
|
Osservazione |
Notiamo che, nella dimostrazione appena conclusa, le ipotesi che f fosse
biiettiva e che fosse un morfismo sono state utilizzate in maniera disgiunta: nel far
vedere che il prodotto operatorio di due isomorfismi è un isomorfismo... e da qui lo
spunto per la definizione di omomorfismo... |
|
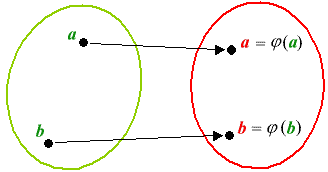
Quando abbiamo due gruppi isomorfi è come se ci trovassimo di fronte a due mondi
paralleli. Per rendere visivamente evidente questo fatto, utilizziamo una notazione
"colorata". Supponiamo infatti di avere due gruppi isomorfi, un gruppo "verde"
(G, °) e un gruppo "rosso" (G, °) e sia j : G ®G un isomorfismo. Il gruppo verde G ha
l'operazione verde ° e il gruppo rosso G ha, pensate
un pò, l'operazione rossa °. Gli elementi che appartengono al gruppo verde G verranno
indicati con lettere verdi, ad esempio scriveremo aÎG. I più
perspicaci avranno già intuito che gli elementi che appartengono al gruppo rosso G
verranno indicati, incredibile dictu, con lettere rosse! Ora ci serve una notazione che
renda visivamente immediata la funzione j : G ® G.
Se aÎG , allora j(a)ÎG e
quindi non c'è miglior notazione che porre a = j(a): |
| j : |
G |
® |
G |
|
a |
® |
a |
|
b |
® |
b |
|
... |
|
... |
|
|
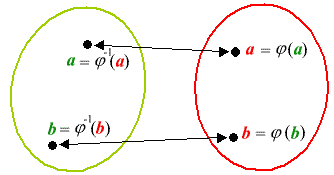
Nella figura seguente
rendiamo più evidente la biiezione j : G ®G |
|
|
L'isomorfismo j : G ®G conserva
le operazioni gruppali: |
j(a°b) = j(a)°j(b) = a°b "a,bÎG |
Eliminando il passaggio
intermedio, si ha dunque, con la nostra notazione, |
j(a°b) = a°b "a,bÎG |
Graficamente
si ha la seguente situazione: |
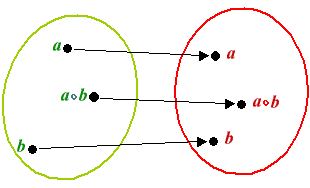 |
Carino, non è vero? Tramite j siamo passati dal mondo verde al
mondo rosso e nel far questo non solo si deve sostituire a
con a e
b con b,
ma anche l'operazione verde ° con
l'operazione rossa ° |
Questo significa che è la
stessa cosa ... |
La j(a°b) = a°b "a,bÎG
si può anche rappresentare con il seguente diagramma commutativo |
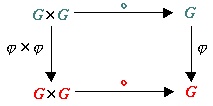
|
dove |
| j xj : |
G x G |
® |
G x G |
|
(a, b) |
® |
(a,
b) |
|
Essendo j : G ® G
un isomorfismo, anche la funzione inversa j -1 : G ®
G è un isomorfismo e quindi |
j
-1(a°b) = a°b "a,bÎG |
|
Un isomorfismo è una biiezione che conserva le operazioni. Tutto qui? Vediamo
come le conseguenze siano molte ed importanti. La proposizione che segue ci fornirà la
risposta.(poi in una osservazione commentare la dimostrazione e far vedere che alcuni
risultati sono validi anche se non si richiede la biiettività). |
Abbandoniamo per il momento
la nostra notazione colorata, torniamo alla tradizione. |
Proposizione |
Siano dati due gruppi
(G, °) e (G',
à) e un isomorfismo j : G®G'
. Risulta |
|
|
|
|
|
|
|
|
|
|
|
|
G è ciclico  G' è ciclico G' è ciclico
|
S<G  j(S)<G'
??? j(S)<G'
???
|
Dim. |
|
Osservazione |
Notiamo che, in alcune dimostrazioni, le ipotesi che j fosse biiettiva e che fosse un morfismo sono state utilizzate in
maniera disgiunta... |
|
|
|
|