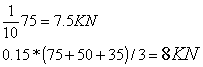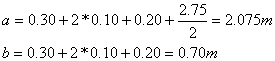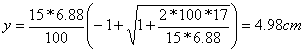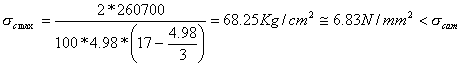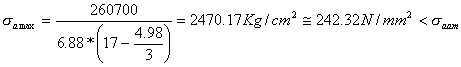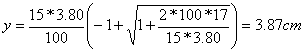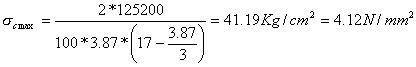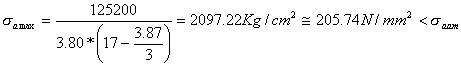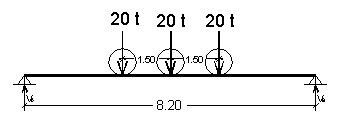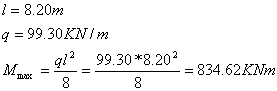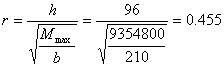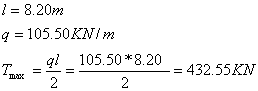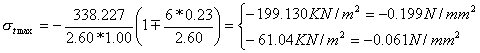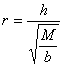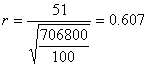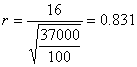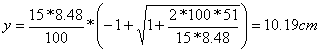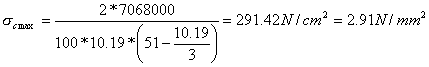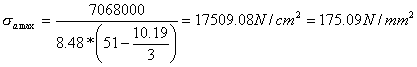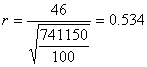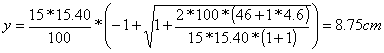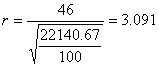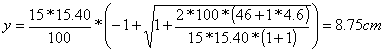PONTICELLO IN CEMENTO ARMATO DI 2^a CATEGORIA

Ponti stradali

Passerella pedonale

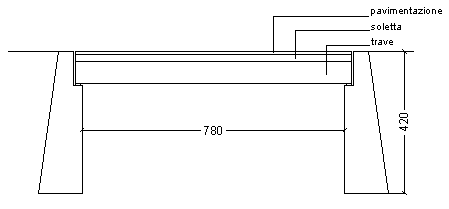
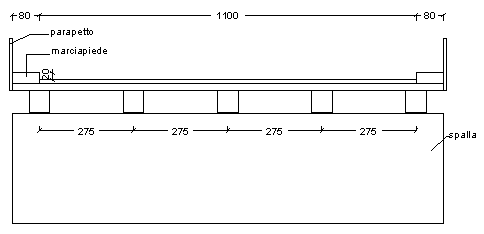
Progetto di un ponticello in cemento armato di 2^a categoria, di luce netta pari a 7.80 m, larghezza di carreggiata di 11.00 m e marciapiedi laterali di 0.80 m. Il piano di posa delle spalle è a - 4.20 m dalla superficie stradale del ponticello.

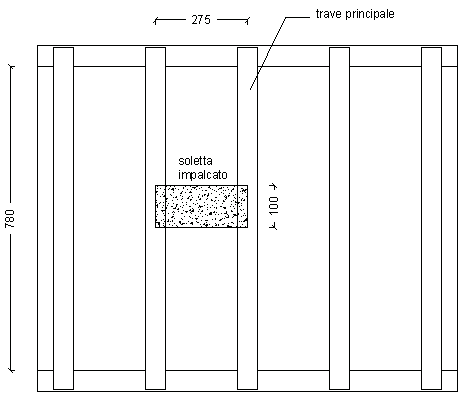
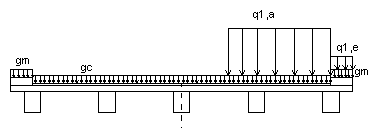
Realizziamo il ponticello con travi principali semplicemente appoggiate sulle spalle, soletta d'impalcato collaborante con le travi, pavimentazione in conglomerato bituminoso. Volendo limitare lo spessore della soletta disponiamo le travi principali ad interasse non superiore a 3 m di luce; pertanto sulla carreggiata larga 11.00 m occorre posare 5 travi principali, con interasse di 2.75 m, e soletta dei marciapiedi a sbalzo.

Per la struttura del ponticello e delle spalle si utilizzano calcestruzzo R_ck 25 ed armature metalliche FeB44k, con le seguenti caratteristiche:

- peso specifico g = 25.00 KN/m³

- tensione ammissibile a flessione s_cam = 8.50 N/mm²

- tensione ammissibile a taglio t_c0 = 0.53 N/mm²

- tensione ammissibile a compressione s_am = 6.0 N/mm²

- modulo elastico E = 28500 N/mm²

Il terreno, a monte delle spalle, possiede le seguenti caratteristiche:

- peso specifico g_t = 18 KN/m³

- angolo attrito interno j = 32°

- coefficiente attrito muro/terra f = 0.6

- portanza del terreno s_am = 0.20 N/mm²

Sezione longitudinale

Sezione traversale

Vista dall'alto

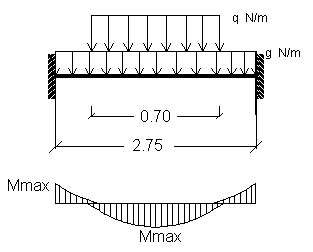
Per ottenere l'interasse reale tra le travi principali, ipotizzando un numero di 5 travi, si ricava:

PROGETTO SOLETTA D'IMPALCATO

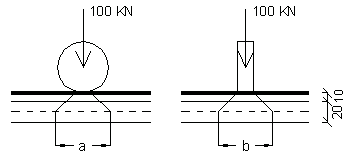
La soletta d'impalcato, pur essendo una struttura iperstatica su 5 appoggi (le travi principali), per semplicità di calcolo, può essere studiata a campata semplice e vincolo di semincastro. Inoltre, poiché il rapporto tra lunghezza (7.80 m) e larghezza (2.75 m) della soletta è maggiore di 1.7 ¸ 1.8, possiamo ritenere valido un comportamento a trave e non a piastra della soletta. Per il calcolo, ipotizziamo di realizzare una pavimentazione in conglomerato bituminoso di spessore 10 cm, ed una soletta piena in c.a. di spessore presunto di 20 cm. Nel progetto, consideriamo il transito di una fila di ruote del mezzo convenzionale q_1,a, ridotto al 75% in quanto ponte di 2^a categoria, nella posizione più gravose per la sollecitazione di flessione che è il punto di mezzo della striscia di soletta, indipendentemente dall'ingombro trasversale del mezzo, come recita l'art. 3.4.4.4 della Normativa. In definitiva, la striscia di soletta è sollecitata:

- dal carico isolato q_1,c di 10 t con impronta quadrata di lato 0.30 m,

- dall'incremento dinamico q₂, pari al 40% in quanto la luce della soletta (2.75 m) è minore di 10 m,

- dall'azione longitudinale di frenamento q₃, con intensità pari a 1/10 della singola colonna di carico più pesante per ciascuna categoria; in tutti i casi essa deve risultare non inferiore al 15% (2^a categoria) del totale del carico q_1,a che può interessare la struttura. L'azione di frenamento agisce nella direzione dell'asse stradale ed al livello della pavimentazione, producendo, in tal modo, un momento torcente rispetto al piano medio della soletta, da valutare separatamente; per semplicità di procedimento possiamo prendere l'azione di frenamento agente perpendicolarmente sul piano della pavimentazione, sommandola ai carichi q₁ e q₂ in modo da avere un incremento dell'effetto flessione.

Analisi dei carichi
carichi permanenti (g)	pavimentazione in conglomerato bituminoso (s =10 cm)
	soletta in cemento armato (s = 20 cm)
	somma carichi g
carichi mobili (q)	carico q1,c
	incremento dinamico q2
	azione di frenamento q3
	somma carichi q

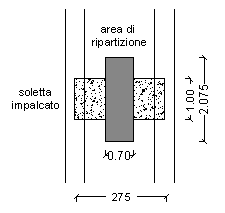
L'area di ripartizione del carico trasmesso da una ruota (ipotesi di Winkler) si ha a livello del piano medio della soletta, su una superficie di lati:

	Nel calcolo a trave, il lato a dell'area di ripartizione deve essere aumentato di una quantità pari a meta della luce della soletta:

La somma del carico q, trasmesso dalla ruota del mezzo convenzionale, viene determinato sul m² dell'area di ripartizione:

Nel calcolo, si considera una striscia di 1 m di soletta, per cui si ha:

carichi permanenti (g)
carichi mobili (q)

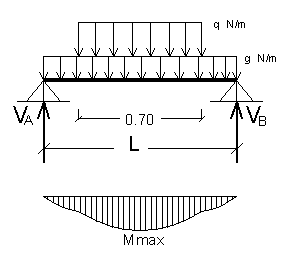
La situazione più sfavorevole, a flessione, si ha con il carico q posto in mezzeria della soletta. Per semplificare la determinazione del massimo momento flettente, la soletta si studia come semplicemente appoggiata agli estremi. Una volta determinato il momento massimo dell'appoggio semplice, può essere facilmente determinato il momento di semincastro in quanto risulta pari a 2/3 del momento di appoggio. Questo perché il momento di una trave semincastrata e carico ripartito uniforme vale 1/12 ql², mentre il momento di una trave appoggiata e carico ripartito uniforme vale 1/8 ql².

Condizione di appoggio semplice	Condizione di semincastro

Determiniamo prima le reazioni vincolari V_A e V_B che, per simmetria, sono uguali:

Il momento massimo, in caso di appoggio semplice, vale:

Determiniamo, ora, il momento di semincastro moltiplicando per 2/3

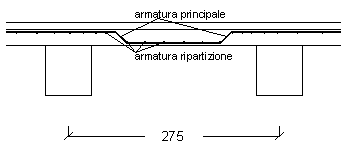
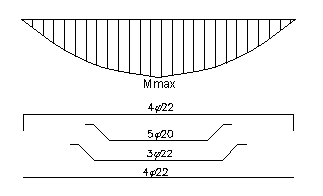
CALCOLO ARMATURA PRINCIPALE

Progettando la soletta, di spessore pari a 20 cm e striscia di 1 m, con armatura semplice (b=0), utilizzando le tabelle di r e t espresse in Kg/cm², e trasformando il valore del momento da KNm in Kgcm, otteniamo:

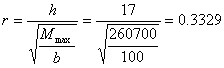
In corrispondenza del coefficiente r, ora ricavato, in tabella otteniamo t @0.00128

L'area dell'acciao, in zona tesa, è:

Possiamo scegliere 2f12 + 3f14 = 6.88 cm² per ogni metro di soletta.

CALCOLO ARMATURA DI RIPARTIZIONE

L'armatura di ripartizione, nelle solette non calcolate come piastra, deve essere disposta ortogonalmente e non deve essere minore al 20% di quella principale necessaria. Pertanto risulta:

Inoltre, l'ipotesi di Winkler impone che nelle solette non calcolate come piastra, l'armatura di ripartizione deve essere in grado di assorbire un momento flettente secondario pari al 25% di quello principale:

Pertanto necessita una quantità di armatura di ripartizione pari a:

Disponiamo, quindi, 4f8/m pari a 2.01 cm²/m

Armatura principale 2f12 + 3f14/m Armatura di ripartizione 4f8/m

VERIFICA A FLESSIONE

Procediamo, ora, alle operazioni di verifica della soletta determinando prima la posizione dell'asse neutro:

	distanza dell'asse neutro dal lembo compresso
	verifica nel calcestruzzo compresso
	verifica nell'acciaio teso

VERIFICA ALLA FRECCIA

La soletta deve verificare anche alla deformazione elastica (freccia). In questo caso, occorre che la freccia massima non superi la freccia teorica che, per semplificare, possiamo prendere pari a 1/500 della luce.

;

Nel caso di una trave isostatica semincastrata agli estremi e con carico ripartito uniforme si ha:

Nel nostro caso, non possiamo utilizzare direttamente la formula ora scritta poiché il carico q agisce solo su una parte della struttura. Possiamo, però, determinare un carico uniforme equivalente in grado di fornire lo stesso momento flettente. Utilizziamo la formula del momento flettente di una trave semincastrata con carico ripartito:

, e quindi

Calcoliamo, prima il momento d'inerzia della soletta ad armatura semplice:

Quindi, la freccia vale:

Verificato a freccia

VERIFICA A TAGLIO

Per la verifica al taglio occorre posizionare il carico mobile q su un lato della soletta, essendo la situazione più gravosa:

carichi permanenti (g)
carichi mobili (q)

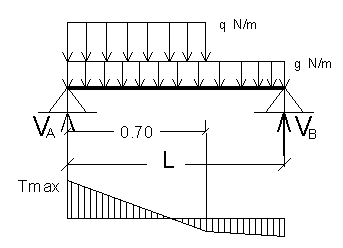
Determiniamo la reazione vincolare V_A, che rappresenta il valore massimo del taglio, calcolando il momento rispetto all'altro vincolo d'estremità:

Verificando a taglio, abbiamo:

Verificato a taglio

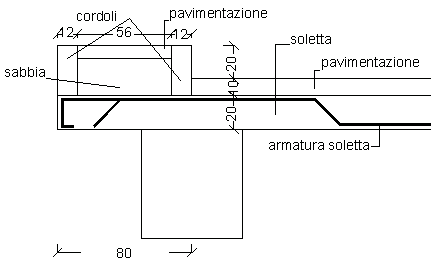
PROGETTO SOLETTA A SBALZO

La soletta del marciapiede è realizzata a sbalzo dalla trave di bordo ed ha una luce di 0.80 m. Rispetto al piano stradale, il marciapiede deve essere rialzato di almeno 20 cm in moda da impedire che una ruota possa gravare sulla soletta del marciapiede. Ipotizziamo di realizzare il marciapiede con due cordoli in calcestruzzo, alti 30 cm e di spessore pari a 12 cm; la pavimentazione del marciapiede si realizza con lastre in calcestruzzo, di spessore 8 cm, posate su un letto di sabbia.

Analisi dei carichi
carichi permanenti (g)	pavimentazione in lastre di cls (s = 8 cm)
	cordoli in calcestruzzo (s = 12 cm)
	sottofondo sabbia (s = 22 cm)
	soletta in cemento armato (s = 20 cm)
carichi mobili (q)	carico q1,d
	incremento dinamico q2
	somma carichi q

Occorre, ora, determinare i valori dei carichi g e q su 1 m lineare di soletta

carichi permanenti (g)
carichi mobili (q)

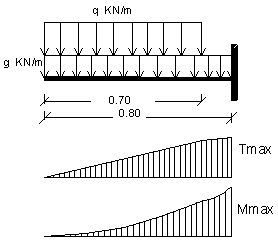
Strutturalmente, la soletta del marciapiede si presenta come una trave a sbalzo, incastrata ad un estremo. I carichi sono uniformemente ripartiti, con il carico q posizionato nella situazione più sfavorevole per la sollecitazione di flessione.

Determiniamo i valori del Taglio massimo e del Momento massimo:

CALCOLO ARMATURA SOLETTA A SBALZO

Lasciando la soletta di spessore pari a 20 cm e striscia di 1 m, con armatura semplice (b=0), utilizzando le tabelle di r e t espresse in Kg/cm², e trasformando il valore del momento da KNm in Kgcm, otteniamo:

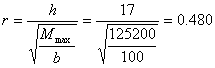
In corrispondenza del coefficiente r, ora ricavato, in tabella otteniamo t @0.000858

L'area dell'acciao, in zona tesa, è:

Occorre rispettare una quantità di armatura minima, pari allo 0.15% della sezione di conglomerato:

Possiamo scegliere 2f12 + 1f14 =3.80 cm² per ogni metro di soletta.

CALCOLO ARMATURA DI RIPARTIZIONE

L'armatura di ripartizione, nelle solette non calcolate come piastra, deve essere disposta ortogonalmente e non deve essere minore al 20% di quella principale necessaria. Pertanto risulta:

Disponiamo, quindi, 2f8/m pari a 1.01 cm²/m

VERIFICA A FLESSIONE

Procediamo, ora, alle operazioni di verifica della soletta a sbalzo determinando prima la posizione dell'asse neutro:

	distanza dell'asse neutro dal lembo compresso
	verifica nel calcestruzzo compresso
	verifica nell'acciaio teso

VERIFICA ALLA FRECCIA

La soletta deve verificare anche alla deformazione elastica (freccia). In questo caso, occorre che la freccia massima non superi la freccia teorica che, per semplificare, possiamo prendere pari a 1/500 della luce.

;

Nel caso di una trave isostatica a sbalzo (incastrata ad un estremo) e con carico ripartito uniforme si ha:

Nel nostro caso, non possiamo utilizzare direttamente la formula ora scritta poiché il carico q agisce solo su una parte della struttura. Possiamo, però, determinare un carico uniforme equivalente in grado di fornire lo stesso momento flettente. Utilizziamo la formula del momento flettente di una trave a sbalzo con carico ripartito:

, e quindi

Calcoliamo, prima il momento d'inerzia della soletta ad armatura semplice:

Quindi, la freccia vale:

Verificato a freccia

VERIFICA A TAGLIO

Verificato a taglio

PROGETTO TRAVE PRINCIPALE

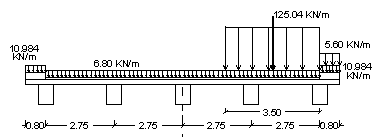
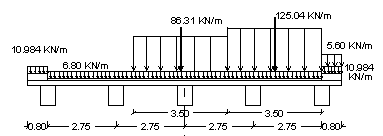
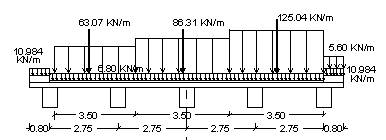
Come detto nella lezione sui ponti stradali, la trave più sollecitata è la trave di bordo e, perciò, determineremo il carico gravante su di essa mediante la formula di Courbon. Occorre stabilire quanti schemi di carico disporre trasversalmente e in quale posizione risultano più gravosi.

	q1,a = carico di una colonna di carico q1,e = carico della folla compatta sul marciapiede gm = carico permanente sul marciapiede gc = carico permanente sulla carreggiata
Sezione trasversale

Conoscendo la luce netta della trave (m 7.80), possiamo determinarne la luce di calcolo assumendo un incremento di circa il 5%:

Ricordando che la larghezza convenzionale di una colonna è di 3.50 m, otteniamo che lungo la carreggiata, larga 11.00 m, possono transitare:

- una prima colonna di carico q1,a, ridotta al 75% (essendo un ponte di 2^a categoria)

- una seconda colonna di carico q1,a, ridotta al 50%

- una terza colonna di carico q1,a, ridotta al 35%

Sui marciapiedi può transitare il carico q1,e della folla compatta.

Determiniamo, ora, il carico q uniforme equivalente, ottenuto dalla conversione del carico concentrato q1,a, sulla luce di calcolo della trave

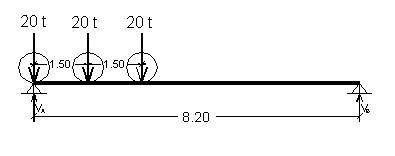
La sollecitazione flessionale più sfavorevole si ha quando il carico trasmesso dai tre assi, del mezzo convenzionale, si trova in mezzeria della trave.

Le reazioni vincolari V_A e V_B sono uguali per effetto della simmetria di carico:

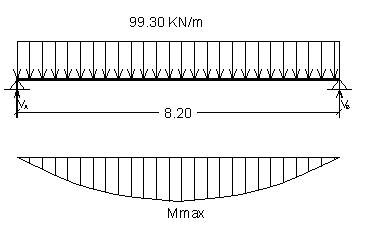
Il momento flettente massimo, in mezzeria, vale:

Il carico ripartito equivalente, a flessione, è:

Pertanto abbiamo:

- carico ripartito equivalente prima colonna : 0.75*110.65 = 82.99 KN/m

- carico ripartito equivalente seconda colonna : 0.50*110.65 = 55.33 KN/m

- carico ripartito equivalente terza colonna : 0.35*110.65 = 38.73 KN/m

Gli stessi valori possono essere ottenuti consultando la tabella di conversione dei carichi isolati q1,a, presente nella lezione sui ponti stradali.

L'incremento dinamico q₂, essendo la luce della trave inferiore a 10 m, è pari al 40% del carico q equivalente:

- incremento dinamico prima colonna : 0.40*82.99 = 33.20 KN/m

- incremento dinamico seconda colonna : 0.40*55.33 = 22.13 KN/m

- incremento dinamico terza colonna : 0.40*38.73 = 15.49 KN/m

L'azione di frenamento, agente nella direzione dell'asse della strada e giacente sulla superficie stradale, deve essere la maggiore tra:

1/10 della singola colonna più pesante
15% del totale del carico gravante sulla struttura	N.B.: 3 è il numero massimo di colonne di carico
L'azione di frenamento vale:

Per l'azione di frenamento vale quanto già detto nel progetto della soletta: essa produce un momento torcente rispetto al piano medio della soletta, da valutare separatamente; per semplicità di procedimento possiamo prendere l'azione di frenamento agente perpendicolarmente sul piano della pavimentazione, sommandola ai carichi q₁ e q₂ in modo da avere un incremento dell'effetto flessione.

Analisi dei carichi
carichi permanenti soletta + marciapiede (gm)
carichi permanenti soletta (gc)
carico mobile 1^a colonna
carico mobile 2^a colonna
carico mobile 3^a colonna
carico folla compatta (compreso effetto dinamico)

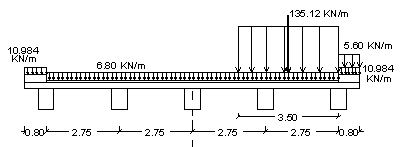
Determiniamo il carico sulla trave di bordo esaminando tre condizioni:

- 1^a condizione: transito di una sola colonna + folla compatta su un marciapiede

Transito di una sola colonna e carico di folla compatta sul marciapiede adiacente

Determiniamo, applicando Varignon, l'eccentricità della risultante dei carichi g e q.

La somma dei carichi vale:

Il momento statico del carico g sui marciapiedi, rispetto alla mezzeria della carreggiata, è nullo. Lo stesso vale per il momento del carico g della carreggiata. Pertanto, abbiamo:

Utilizzando la formula di Courbon, otteniamo il carico, a metro lineare, sulla trave di bordo:

Carico sulla trave di bordo (1^a condizione)

- 2^a condizione: transito di due colonne + folla compatta su un marciapiede

Transito di due colonne e carico di folla compatta sul marciapiede adiacente

La somma dei carichi vale:

Applicando Varignon, si ha:

Utilizzando la formula di Courbon, otteniamo il carico, a metro lineare, sulla trave di bordo:

Carico sulla trave di bordo (2^a condizione)

- 3^a condizione: transito di tre colonne + folla compatta su un marciapiede

Transito di tre colonne e carico di folla compatta sul marciapiede adiacente

La somma dei carichi vale:

Applicando Varignon, si ha:

Utilizzando la formula di Courbon, otteniamo il carico, a metro lineare, sulla trave di bordo:

Carico sulla trave di bordo (3^a condizione)

Risulta, quindi, più gravoso il transito di due colonne.

La trave di bordo, sollecitata dal carico ripartito uniforme di 99.30 KN/m, è semplicemente appoggiata sulle spalle. Lo schema strutturale è il seguente:

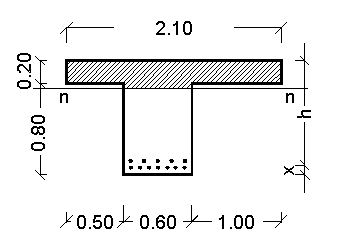
La trave risulta solidale con la soletta. Pertanto, come impone l'art. 5.5 delle norme sul cemento armato, occorre determinare la larghezza di soletta collaborante da ciascun lato della trave. La norma impone che la striscia di soletta collaborante sia pari alla maggiore fra le dimensioni seguenti:

- un decimo della luce della nervatura

- cinque volte lo spessore della soletta più una volta la larghezza dell'eventuale raccordo della soletta

In nessun caso la larghezza di soletta collaborante da ciascun lato può superare la dimensione fra la sezione in esame e quella in cui ha termine la soletta, né la metà della luce fra le nervature.

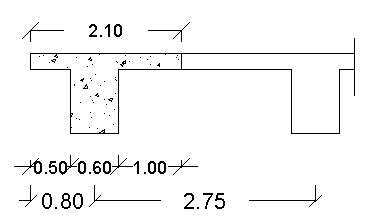
Ipotizzando una base di trave pari a 0.60 m, la striscia collaborante (1.00 m) non può superare: Nello sbalzo; Nella campata:

Per quanto riguarda le tensioni ammissibili nel calcestruzzo, occorre ricordare quanto impone l'art. 3.1.3: "Nelle travi a T con soletta collaborante la tensione ammissibile è ridotta del 30% per soletta di spessore s<5 cm, del 10% per soletta di spessore s>=5 cm."

Avendo inizialmente stabilito di utilizzare calcestruzzo di classe R_ck 25, risulta:

Volendo utilizzare le tabelle dei coefficienti r e t con i valori espressi in Kg e in cm, occorre trasformare il valore del momento flettente e della tensione ammissibile:

M_max = 8346200 s_am = 76 Kg/cm²

Determiniamo l'altezza utile della trave, ad armatura semplice, sapendo che la larghezza di calcestruzzo compresso è b = 2.10 m:

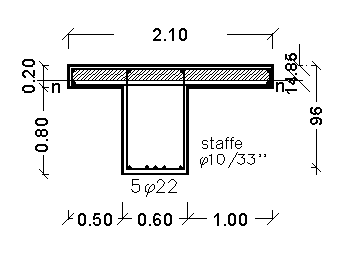
Dovendo considerare anche il peso della nervatura e volendo rendere più rigida la trave, per limitare la deformazione elastica, si porta l'altezza della nervatura a 80 cm; quindi l'altezza complessiva della trave a T è di 1.00 m.

Il peso della nervatura è:

Il momento massimo diventa:

Avendo aumentato l'altezza della trave, possiamo avere un risparmio in armatura metallica determinando il coefficiente t in funzione del nuovo valore di r:

a questo valore di r, corrisponde in tabella il coefficiente t = 0.000911

L'area acciaio è:

Scegliamo questi ferri: 5f20 + 7f22 per un'area complessiva A_a = 42.32 cm². I ferri vengono disposti su due file: nella prima fila si posizionano i 7f22 (26.61 cm²) alla distanza di 4 cm dal lembo esterno, nella seconda i 5f20 (15.71 cm²) alla distanza di 8 cm, sempre dal lembo esterno. Determiniamo il baricentro delle armature tese, calcolando la distanza dal lembo teso, mediante Varignon:

e quindi

Le armature metalliche, ora calcolate, devono essere disposte nella sezione di mezzeria dove il momento è massimo. Ma ricordando che anche nelle sezioni in cui il momento assume valori minimi, occorre garantire una sezione di acciaio minimo pari allo 0.15% della sezione di conglomerato, calcoliamo:

	Sezione del calcestruzzo
	Area minima dell'acciaio
	Ferri dritti
	Ferri sagomati

VERIFICA A FLESSIONE

Sezione reagente trave di bordo	Schema longitudinale dei ferri

Determiniamo la distanza dell'asse neutro dal lembo compresso:

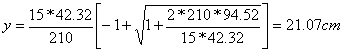
Poiché la distanza dell'asse neutro dal lembo compresso supera lo spessore della soletta, occorre rideterminarne la posizione, mediante la formula per le travi a T soggette a Momento positivo. Per ottenere la distanza y, risolviamo la seguente equazione di 2° grado:

Le soluzioni sono:

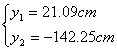
Scartando la soluzione negativa, la distanza da utilizzare nelle verifiche è: y = 21.09 cm.

Determiniamo, ora, il momento d'inerzia della sezione reagente rispetto all'asse neutro:

Verificando a flessione, nel calcestruzzo abbiamo:

Verifica a flessione nel calcestruzzo

Nell'acciaio teso, abbiamo:

	Verifica a flessione nell'acciaio

VERIFICA ALLA FRECCIA

La trave deve verificare anche alla deformazione elastica (freccia). Pertanto, occorre che la freccia massima non superi la freccia teorica.

;

Nel caso di una trave isostatica appoggiata agli estremi e con carico ripartito uniforme si ha:

Il momento d'inerzia della sezione di trave, già calcolato nella verifica a flessione, vale:

Il carico ripartito uniforme sulla trave è dato dalla somma del carico q e del peso proprio P_p della nervatura:

Quindi, la freccia vale:

Verificato a freccia

VERIFICA A TAGLIO

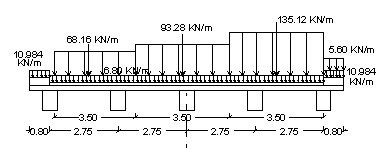
Determiniamo il carico q uniforme equivalente, ottenuto dalla conversione del carico concentrato q1,a, sulla luce di calcolo della trave

La sollecitazione di taglio più sfavorevole si ha quando il carico trasmesso dai tre assi, del mezzo convenzionale, si trova in prossimità di un appoggio della trave.

Le reazioni vincolari V_A è maggiore della reazione V_B. Determiniamo il valore di V_A tramite l'equazione di equilibrio alle rotazioni rispetto all'appoggio B, esprimendo i carichi in KN:

Il carico ripartito equivalente, a taglio, vale:

Pertanto abbiamo:

- carico ripartito equivalente prima colonna : 0.75*119.57 = 89.68 KN/m

- carico ripartito equivalente seconda colonna : 0.50*11.57 = 59.79 KN/m

- carico ripartito equivalente terza colonna : 0.35*119.57 = 41.85 KN/m

Gli stessi valori possono essere ottenuti consultando la tabella di conversione dei carichi isolati q1,a, presente nella lezione sui ponti stradali.

L'incremento dinamico q₂, essendo la luce della trave inferiore a 10 m, è pari al 40% del carico q equivalente:

- incremento dinamico prima colonna : 0.40*89.68 = 35.87 KN/m

- incremento dinamico seconda colonna : 0.40*59.79 = 23.92 KN/m

- incremento dinamico terza colonna : 0.40*41.85 = 16.74 KN/m

L'azione di frenamento, agente nella direzione dell'asse della strada e giacente sulla superficie stradale, deve essere la maggiore tra:

- 1/10 della singola colonna più pesante
- 15% del totale del carico gravante sulla struttura	N.B.: 3 è il numero massimo di colonne di carico
L'azione di frenamento vale:

Analisi dei carichi
carichi permanenti soletta + marciapiede (gm)
carichi permanenti soletta (gc)
carico mobile 1^a colonna
carico mobile 2^a colonna
carico mobile 3^a colonna
carico folla compatta (compreso effetto dinamico)

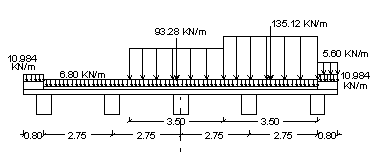
Determiniamo il carico sulla trave di bordo esaminando tre condizioni:

- 1^a condizione: transito di una sola colonna + folla compatta su un marciapiede

Transito di una sola colonna e carico di folla compatta sul marciapiede adiacente

Determiniamo, applicando Varignon, l'eccentricità della risultante dei carichi g e q.

La somma dei carichi vale:

Il momento statico del carico g sui marciapiedi, rispetto alla mezzeria della carreggiata, è nullo. Lo stesso vale per il momento del carico g della carreggiata. Pertanto, abbiamo:

Utilizzando la formula di Courbon, otteniamo il carico, a metro lineare, sulla trave di bordo:

Carico sulla trave di bordo (1^a condizione)

- 2^a condizione: transito di due colonne + folla compatta su un marciapiede

Transito di due colonne e carico di folla compatta sul marciapiede adiacente

La somma dei carichi vale:

Applicando Varignon, si ha:

Utilizzando la formula di Courbon, otteniamo il carico, a metro lineare, sulla trave di bordo:

Carico sulla trave di bordo (2^a condizione)

- 3^a condizione: transito di tre colonne + folla compatta su un marciapiede

Transito di tre colonne e carico di folla compatta sul marciapiede adiacente

La somma dei carichi vale:

Applicando Varignon, si ha:

Utilizzando la formula di Courbon, otteniamo il carico, a metro lineare, sulla trave di bordo:

Carico sulla trave di bordo (3^a condizione)

Anche nella sollecitazione tagliante risulta più gravoso il transito di due colonne.

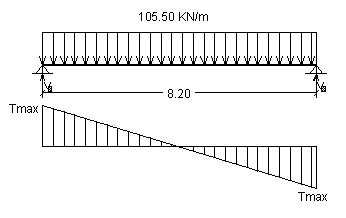
La trave di bordo, sollecitata dal carico ripartito uniforme di 105.50 KN/m, è semplicemente appoggiata sulle spalle. Lo schema strutturale è il seguente:

Avendo già progettato a flessione la trave, occorre sommare il peso della nervatura (12 KN/m) al carico q. Pertanto abbiamo:

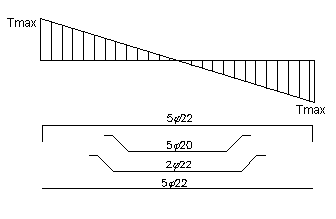
Ricordiamo che alle estremità delle travi deve essere disposta un'armatura inferiore in grado di assorbire uno sforzo uguale al taglio. Pertanto calcoliamo la quantità di armatura da lasciare diritta in zona tesa:

Decidiamo di lasciare dritti 5f22 e di sagomare 2f22 + 5f20

Ferri dritti Ferri sagomati

Determiniamo la posizione dell'asse neutro nella sezione di appoggio, sollecitata a taglio massimo, in cui, in zona tesa, sono collocati 5f22 e la zona compressa risulta larga 210 cm:

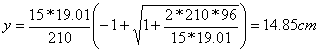
Notiamo che l'asse neutro passa nello spessore della soletta, quindi possiamo verificare come se la sezione fosse rettangolare. Determiniamo la tensione tangenziale:

Essendo t_cmax < t_co non occorre calcolare le armature resistente al taglio (ferri sagomati e staffe), ma è necessario disporre almeno tre staffe a metro. Pertanto disporremo le staffe con un intervallo di:

Sezione della trave di bordo in prossimità dell'appoggio sulle spalle.

PROGETTO APPOGGIO TRAVE PRINCIPALE

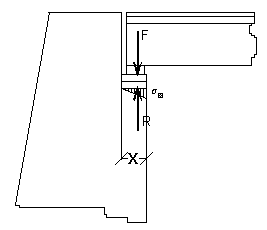
Vogliamo, ora, determinare la profondità x della sede di appoggio della trave sulla spalla. Supponendo che, nella situazione più sfavorevole, il carico F trasmesso dalla trave, di base 60 cm, cada al limite del terzo medio della zona di appoggio, abbiamo una ripartizione triangolare delle tensioni s sulla spalla. Per l'equilibrio, la forza R di reazione della muratura deve essere almeno uguale alla forza F e passare per la stessa retta di direzione.

Utilizzando calcestruzzo R_ck 25, possiamo assumere come tensione ammissibile nel calcestruzzo compresso il valore s_c @ 6 N/mm². La forza di reazione R, vale:

deve essere uguale alla forza agente F, pertanto:

e quindi:

Per avere una situazione d'appoggio più favorevole, portiamo la distanza x a 35 cm.

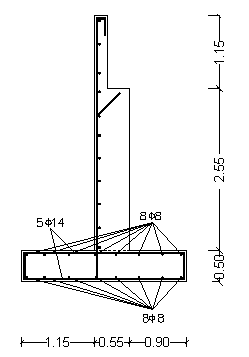
PROGETTO SPALLA IN CEMENTO ARMATO

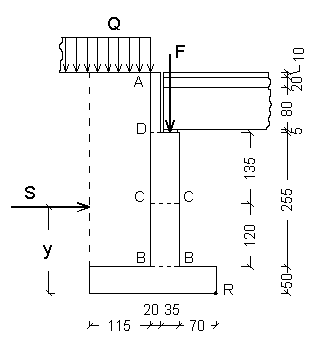
La spalla, in conglomerato cementizio armato, si realizza con paramento interno verticale. Il terrapieno, orizzontale, è gravato uniformemente dal carico q_1,a dovuto al mezzo convenzionale di 600 KN, il cui ingombro è di 15 m x 3.50 m. La sezione del muro di spalla, formata da una parete verticale ed un solettone di base, si scompone in tre rettangoli. L'azione spingente si determina, mediante la formula di Coulomb, sul paramento verticale fittizio passante per il punto a monte della base.

L'altezza complessiva del muro è h = 4.20 m La risega della spalla, per l' appoggio della trave, è alta 1.15 m, ottenuta dalla somma dello spessore della pavimentazione (10 cm), della soletta (20 cm), della nervatura della trave (80 cm) e dello spessore del dormiente (@ 5 cm) Il sovraccarico sul terrapieno, dovuto al transito del carico q1,A è:

L'azione F trasmessa dalla trave di bordo, su 1 m di profondità di muro, vale:

Questa forza, verticale, deve essere presa in considerazione solamente nelle situazioni più sfavorevoli, e cioè:

- nella verifica a ribaltamento risulta a favore della stabilità, pertanto non si considera

- nella verifica a scorrimento risulta a favore della stabilità, pertanto non si considera

- nella verifica a schiacciamento risulta a sfavore della stabilità, occorre prenderla in considerazione.

PROGETTO DIMENSIONI PARETE E SOLETTONE

Le dimensioni sono determinate mediante un predimensionamento di massima:

	spessore alla sommità della parete
	spessore alla base della parete verticale (arrotondato per eccesso per tenere conto della larghezza della sede di appoggio della trave)
	lunghezza intero solettone (arrotondato per eccesso in modo da favorire la verifica a schiacciamento)
	lunghezza solettone interno (arrotondato per difetto in modo da non gravare troppo a schiacciamento)
	lunghezza solettone esterno
	altezza del solettone

VERIFICHE DI STABILITÀ DELLA SPALLA

Prima di procedere con il calcolo delle armature metalliche nella parete verticale e nel solettone di base, è consigliabile controllare se il predimensionamento dell'intero manufatto garantisce la stabilità al ribaltamento, allo scorrimento e allo schiacciamento.

Iniziamo calcolando la spinta S sul paramento fittizio verticale utilizzando il metodo di Coulomb. Prima trasformiamo il sovraccarico in altezza fittizia di terra:

La distanza della spinta S dalla base del muro è:

Il momento spingente M_S sulla spalla è dato da:

VERIFICA A RIBALTAMENTO

La verifica a ribaltamento, intorno al punto R del solettone esterno, è garantita se risulta:

Ricordando che la forza F, scaricata dalla trave sulla spalla, è a favore della stabilità nella verifica a ribaltamento, il momento resistente M_R vale:

Determiniamo le distanze d dei pesi P dal punto R

Il momento resistente M_R, ora, vale:

Verificato a ribaltamento

VERIFICA A SCORRIMENTO

Anche nella verifica a scorrimento la forza F è a favore della stabilità, per cui non si prende in considerazione. La somma dei pesi è:

Verificato a scorrimento

VERIFICA A SCHIACCIAMENTO

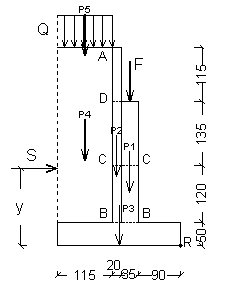
Nella verifica a schiacciamento occorre, invece, considerare la forza F in quanto procura una condizione più gravosa. Considerando la forza F applicata nel punto medio della sede d'appoggio, determiniamo il momento resistente M_R

La verifica a schiacciamento sul terreno risulta soddisfatta quando

Determiniamo la distanza u della forza risultante dal punto R di massima compressione:

Controlliamo se la risultante cade dentro o fuori del terzo medio:

Essendo u>b_s/3 la risultante risulta interna al terzo medio. Utilizziamo la formula di verifica a presso flessione:

L'eccentricità e vale:

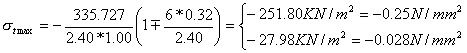
Essendo s_tmax > s_tam la verifica a schiacciamento non è soddisfatta.

Possiamo aumentare la lunghezza del solettone esterno di 20 cm, portando la lunghezza a 0.90 m. Occorre ricalcolare il peso P₃ del solettone di base e le nuove distanze d dal punto R.

Rideterminiamo la sommatoria dei pesi ed il momento resistente M_R:

Determiniamo la distanza u della forza risultante dal punto R di massima compressione:

Controlliamo se la risultante cade dentro o fuori del terzo medio del solettone:

Essendo u>b_s/3 la risultante risulta interna al terzo medio. Calcoliamo l'eccentricità:

Verificando a presso flessione si ha:

Verificato a schiacciamento

Passiamo, ora, al progetto delle armature metalliche nella parete verticale e nel solettone di base.

PROGETTO ARMATURE PARETE VERTICALE

La parete verticale è studiata come una mensola incastrata alla base e soggetta al carico rappresentato dal diagramma delle pressioni del terrapieno.

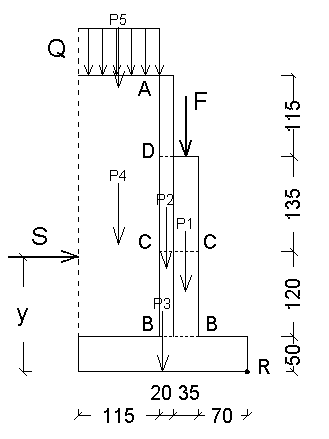
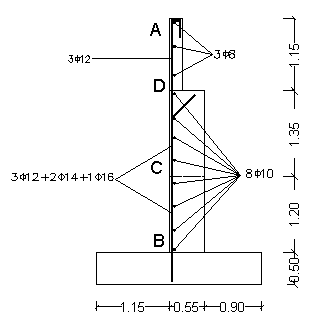
Per semplicità, gli sforzi di taglio T e di momento flettente M sono calcolati prendendo in esame alcune sezioni caratteristiche (il numero è in relazione all’altezza della parete, comunque almeno tre, compresa la sezione di attacco sul solettone). Sulla parete si individuano le sezioni: B-B alla base della parete C-C a 1.20 m dalla base D-D alla risega parete A-A in sommità della parete

In seguito si calcolano le spinte sulla parete di altezza AB – AC – AD rispettivamente e i relativi punti di applicazione mediante le note formule:

	intensità della spinta di un terrapieno con sovraccarico
	distanza del punto d’applicazione della spinta dalla base

Ottenendo, così:

Spinta S (KN/m)	Distanza y (m)

Taglio T (KN)	Momento flettente M (KNm)

Avendo già stabilito le caratteristiche dei materiali R_ck e FeB, imponendo la tipologia ad armatura semplice, in queste sezioni si calcolano i ferri necessari a flessione, non prima di aver determinato il coefficiente r ed il relativo coefficiente t tabellati, necessari per applicare le seguenti formule:

Dati	coefficiente r	coefficiente t	Area acciaio teso (cm^2)
h spessore utile parete nella sezione b 1 m di profondità della parete M momento flettente nella sezione		t (letto in tabella)

ricordando di non scendere sotto la quantità minima di acciaio, pari allo 0.15% della sezione di conglomerato.

Lungo la parete deve essere sempre prevista un’armatura trasversale di ripartizione, almeno pari al 20% dei ferri longitudinali necessari.

PROGETTO ARMATURA SEZIONE B - B

in tabella leggiamo t = 0.000679

L'area acciaio teso è:

La quantità minima di acciaio deve essere:

Nella sezione B-B della parete disponiamo: 3f12+2f14+1f16=8.48 cm²

L'armatura di ripartizione tra la sezione B-B e la sezione C-C deve essere:

utilizziamo 3f10 /m

PROGETTO ARMATURA SEZIONE C - C

Anche nella sezione C-C, pur essendo sollecitata da un momento flettente pari a 25.28 KNm, nettamente minore del momento in B-B, occorre collocare la percentuale minima di ferri.

Nella sezione C-C disponiamo le stesse armature della sezione B-B: 3f12+2f14+1f16=8.48 cm²

L'armatura di ripartizione tra la sezione C-C e la sezione D-D deve essere:

utilizziamo 3f10 /m

PROGETTO ARMATURA SEZIONE D - D

Nella sezione D-D lo spessore della parete è di 20 cm.

in tabella apprezziamo il valore t = 0.0005

L'area acciaio teso è:

La quantità minima di acciaio deve essere:

Nella sezione D-D della parete disponiamo: 3f12 = 3.39 cm²

L'armatura di ripartizione tra la sezione D-D e la sezione A-A deve essere:

utilizziamo 2f8 /m

Disegno dei ferri longitudinali e delle armature di ripartizione nella parete verticale

Si procede, quindi, alle usuali operazioni di verifica a flessione e taglio:

VERIFICA A FLESSIONE NELLA SEZIONE DI BASE DELLA PARETE VERTICALE

	distanza dell’asse neutro dal lembo compresso
	verifica a flessione nel calcestruzzo compresso
	verifica a flessione nell’acciaio teso

VERIFICA A TAGLIO NELLA SEZIONE DI BASE DELLA PARETE VERTICALE

verifica a taglio nel calcestruzzo compresso

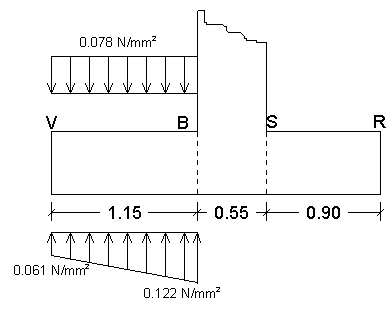
PROGETTO ARMATURA SOLETTONE

Il solettone di base è progettato in due parti: - mensola esterna S-R - mensola interna B-V entrambi le mensole sono incastrate sui piani verticali ottenuti dal prolungamento della parete verticale. Occorre determinare le tensioni in corrispondenza dei punti S (mensola esterna) e B (mensola interna).

La tensione in corrispondenza del punto S si ottiene dalla seguente proporzione:

La tensione in corrispondenza del punto B si ottiene dalla seguente proporzione:

ARMATURE SOLETTONE ESTERNO

Utilizziamo: - armatura doppia simmetrica b = 1 - acciaio FeB44K sa =255 N/mm^2 - calcestruzzo Rck 25 sc = 8.5 N/mm^2 - tc0 = 0.53 N/mm^2 Trascuriamo il peso proprio del solettone, in quanto risulta a favore della stabilità.

Il momento flettente, in corrispondenza della sezione d'incastro S vale:

Calcoliamo il coefficiente r ed in seguito, in tabella, ricerchiamo t per ottenere l'area acciaio teso

t=0.00077

Controlliamo l'area acciaio minima:

scegliamo 5f14 = 7.70 cm^2

L'armatura di ripartizione dovrà risultare:

scegliamo 3f8/m =1.51 cm^2/m

VERIFICA A FLESSIONE NEL SOLETTONE ESTERNO

	distanza dell’asse neutro dal lembo compresso
	Momento d'inerzia della sezione reagente
	verifica a flessione nel calcestruzzo compresso
	verifica a flessione nell’acciaio teso
	verifica a flessione nell’acciaio compresso

VERIFICA A TAGLIO NEL SOLETTONE ESTERNO

verifica a taglio nel calcestruzzo compresso

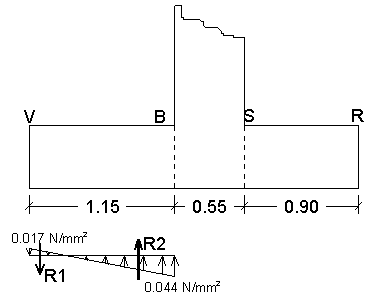
ARMATURE SOLETTONE INTERNO

	Utilizziamo, anche in questo caso, armatura doppia simmetrica b = 1. Trascuriamo, ancora, il peso proprio del solettone Il solettone interno è gravato, dall'alto verso il basso, dal peso del terrapieno P4 e dal sovraccarico P5; dal basso verso l'alto, dalla reazione del terreno sollecitato a schiacciamento. La tensione indotta dal terrapieno e dal sovraccarico vale:
	Il diagramma delle tensioni risultanti sulla mensola interna è dato da: Determiniamo il punto in cui il diagramma s vale zero mediante la seguente proporzione:

Il momento flettente, in corrispondenza della sezione d'incastro B vale:

Calcoliamo il coefficiente r ed in seguito, in tabella, ricerchiamo t per ottenere l'area acciaio teso

t@0.0004

Controlliamo l'area acciaio minima:

scegliamo 5f14 = 7.70 cm^2

L'armatura di ripartizione dovrà risultare:

scegliamo 3f8/m =1.51 cm^2/m

VERIFICA A FLESSIONE NEL SOLETTONE INTERNO

	distanza dell’asse neutro dal lembo compresso
	Momento d'inerzia della sezione reagente
	verifica a flessione nel calcestruzzo compresso
	verifica a flessione nell’acciaio teso
	verifica a flessione nell’acciaio compresso

VERIFICA A TAGLIO NEL SOLETTONE INTERNO

verifica a taglio nel calcestruzzo compresso

Disegno dei ferri longitudinali e delle armature di ripartizione nel solettone di base