.. .. Spazio vettoriale Considerando l'insieme dei vettori su detto insieme si sono definite due operazioni:

• Prodotto di un numero per un vettore

• Somma di vettori

Prodotto di un vettore per un numero.

Assegnato un vettore a definiamo il vettore Ka il vettore che ha la stessa direzione del vettore a modulo pari a K volte il modulo di a ed avente lo stesso verso di a se K è un numero positivo, con verso opposto se K è negativo.

SOMMA DI VETTORI

2.1 Somma di vettori

Per comodità è possibile definire con origine l'estremo del vettore non munito di freccia e con estremo superiore quello che reca la freccia. Occorre notare che l'origine non è il punto di applicazione perché si parla ora di vettori liberi.

Per sommare due vettori utilizzeremo la legge del parallelogramma avente per lati successivi i due vettori. Il vettore somma è il vettore che coincide con la diagonale del parallelogramma avente l'origine coincidente con quello dei due vettori. 

.

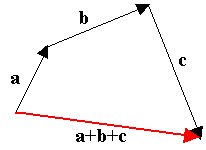
Se la somma riguarda più di due vettori, useremo la regola del poligono funicolare. 

Verifichiamo ora che lo spazio vettoriale ha struttura di gruppo rispetto all'operazione somma.

E' sicuramente verificata la prima richiesta in quanto l'operazione somma associa sempre a due vettori un terzo vettore appartenente allo spazio definito. (Vale per tutti e tre i casi analizzati: la somma di due vettori appartenenti ad uno stesso piano è ancora un vettore appartenente allo stesso insieme).

Definendo il vettore nullo O come quel vettore avente modulo = 0 avremo sempre che scelto un qualsiasi altro vettore a si avrà sempre 

• a + O = O + a = a  

Scelto un qualsiasi vettore a è sempre definire il suo opposto -a per cui

•  a + -a = O

Vale sempre la proprietà associativa 

• a + ( b + c) = (a + b) + c

Vale la proprietà commutativa:

•  a + b = b + a

Pertanto l'insieme dei vettori è un gruppo abeliano rispetto all'operazione somma. Questo implica che è sempre possibile effettuare sull'insieme dei vettori l'operazione inversa all'operazione somma ( la sottrazione).

Linearità dello spazio vettoriale.

Un vettore è sempre esprimibile quale combinazione lineare di altri vettori.

v = K₁ a + K₂ b + K₃ c + K₄ d + K₅ e + ...

Come tutte le differenze è definita come somma di minuendo con l'opposto del sottraendo (in pratica: a-b=a + (-b)). Il vettore differenza è ottenibile facendo coincidere i due estremi superiori dei vettori di cui si vuole la differenza ed è rappresentato da quel vettore che ha origine coincidente con l'origine del minuendo.

 

 

..

..