5.3  Cenni di termodinamica

È possibile ottenere una comprensione molto più completa della fisica dei buchi neri, se si prendono in considerazione, oltre che le loro proprietà gravitazionali, anche quelle termodinamiche.

Poiché la gravità è una forza sempre attrattiva, esiste una tendenza naturale per i sistemi autogravitanti a crescere, piuttosto che a ridursi. Nel caso dei buchi neri, nessuna particella può uscire dall'orizzonte, cosicché esso agisce come una sorta di membrana ad un senso: le particelle possono cadere nel buco e renderlo più grande, ma non uscire, in modo che diventi più piccolo.

Questo fatto portò Bekenstein nel 1972 ad associare la grandezza sempre crescente di un buco nero alla seconda legge della termodinamica, secondo cui esiste una tendenza asimmetrica unidirezionale nella crescita di entropia. Nello stesso anno Hawking perfezionò l'intuizione, dimostrando che, da un punto di vista classico, l'area della superficie dell'orizzonte degli eventi non può decrescere in alcun processo, cioè:

$$\frac{dA}{dt} \ge 0 \; .$$ (5.44)

 

Questo teorema implica il risultato fondamentale che un singolo buco nero non può mai biforcarsi in due più piccoli.

Nel caso generale di buchi neri che possiedono carica elettrica o magnetica Q e momento angolare J, l'area dell'orizzonte dipende da M, Q e J secondo la formula di Smarr [2] (c = G = 1):

$$A = 4\pi \left[ 2M^2 - Q^2 +2M^2\left( 1 - \frac{Q^2}{M^2} - \frac{J^2}{M^4} \right)^{1/2} \right] .$$ (5.45)

 

Tuttavia l'associazione dell'area dell'orizzonte all'entropia del buco nero porta ad alcune difficoltà fondamentali. Infatti, se un buco nero possiede entropia, deve essere caratterizzato anche da una temperatura, e dovrebbe quindi emettere uno spettro di radiazione. Questo, naturalmente, contrasterebbe con la sua stessa definizione di essere nero, e non poter emettere alcun tipo di radiazione.

Non c'è modo di risolvere questo problema classicamente. Infatti, secondo la teoria classica, il buco nero, oltre ad avere temperatura nulla, dovrebbe avere anche entropia infinita.

I problemi della entropia infinita e delle temperatura nulla si possono risolvere se si tiene conto della natura quantistica della materia.

Nel 1974 Hawking dimostrò che i buchi neri non sono neri: essi irradiano energia in modo continuo. La dimostrazione si basa sull'applicazione della meccanica quantistica ai campi elettromagnetici vicino ad un buco nero. Infatti i fotoni, che finora abbiamo classicamente considerato come particelle che seguono traiettorie geodetiche nello spazio-tempo, in accordo al principio di indeterminazione di Heisenberg, non possono essere localizzati con precisione arbitraria. Vicino all'orizzonte, questo fatto cambia drasticamente il comportamento dei fotoni reali da ciò che avviene per particelle idealizzate di massa nulla. Senza entrare nei dettagli del calcolo di Hawking, che usa le tecniche della teoria dei campi quantistica su uno spazio tempo curvo, delineeremo solo le fasi essenziali del ragionamento.

Una forma del principio di indeterminazione è data dalla (1.2):

$$\Delta E \cdot \Delta t \ge h \; ,$$

dove $\Delta E$ è l'indeterminazione minima nell'energia di una particella che risiede in uno stato quantistico per un tempo $\Delta t$. Pertanto lo spazio ordinario è caratterizzato da fluttuazioni del vuoto nei campi elettromagnetici, che consistono di coppie di fotoni prodotti in un evento e che si ricombinano in un altro. Tali coppie violano la conservazione dell'energia, ma non violano alcuna legge fisica, se hanno una durata inferiore al tempo $\Delta t \simeq h / \Delta E$. Ora, come detto in precedenza, lo spazio-tempo vicino all'orizzonte di un buco nero è perfettamente regolare e, in particolare localmente piatto, perciò queste fluttuazioni saranno presenti anche in questa regione. Se si considera una fluttuazione che produce due fotoni, uno di energia Ee l'altro di energia -E, nello spazio-tempo piatto il fotone ad energia negativa non sarebbe in grado di propagarsi liberamente, e si ricombinerebbe con uno ad energia positiva entro il tempo $t \simeq h/E$. Ma, se creato appena fuori dell'orizzonte, ha la possibilità di attraversarlo prima che trascorra questo tempo. Una volta all'interno dell'orizzonte, esso può propagarsi liberamente, in quanto - come ad esempio visto nel caso della metrica di Schwarzschild - in questa regione la coordinata tempo t è una coordinata spaziale, pertanto l'energia negativa del fotone in questa regione è legata soltanto al segno della quantità di moto. Il risultato netto è che un fotone viene creato. Il calcolo rigoroso di Hawking, basato su una approssimazione semiclassica, mostra che, nel caso di Schwarzschild, i fotoni vengono emessi con uno spettro caratteristico di corpo nero, con una temperatura:

$$T = \frac{h}{8 \pi k M} \; ,$$ (5.46)

 

dove k è la costante di Boltzmann.

I buchi neri perciò non sono neri, ma emettono radiazione in modo continuo, con una temperatura inversamente proporzionale alla loro massa. Si noti che, solo nel caso classico per $h \to 0$, si riottiene che il buco è perfettamente nero (T = 0).

Una conseguenza della radiazione di Hawking è che un buco nero, irradiando, tende a perdere energia, e quindi massa, provocando l' ``evaporazione'' e infine la scomparsa dello stesso.

Nel caso di un buco nero di Reissner-Nordström, invece, la temperatura è data da:

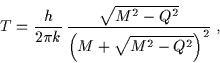$$T = \frac{h}{2 \pi k} \, \frac{\sqrt{M^2 - Q^2}}{\left(M + \sqrt{M^2 - Q^2} \right)^2} \; ,$$ (5.47)

 

ed esiste uno stato Q = M, detto estremo, che corrisponde a temperatura nulla. Il processo di evaporazione in questo caso si arresterà quando la massa del buco nero raggiunge tale valore.

Su basi quantistiche è possibile osservare come anche l'entropia di un buco nero debba mantenersi finita. Infatti non si possono scegliere particelle di energia arbitrariamente piccola per costituire un buco nero, come si può vedere ancora dal principio di indeterminazione. Se questo viene espresso nella forma (c = 1):

$$\Delta \lambda \cdot \Delta E \ge h \; ,$$

allora la lunghezza d'onda $\lambda$ di de Broglie associata alla particella deve essere minore del diametro del buco nero. Per esempio, per un buco nero di Schwarzschild, dovrà essere $\lambda \simeq 2M$ (G = c =1), e l'energia minima della particella dell'ordine $E \simeq h/M$. In questo caso il numero massimo di particelle che possono costituire un buco nero di massa M sarà:

$$N \simeq \frac{M}{E} \simeq \frac{M^2}{h} \; .$$  

Una stima dell'entropia è dunque:

$$S \simeq k N \simeq \frac{k}{h} M^2 \; .$$  

In particolare per un buco nero di Schwarzschild, l'area dell'orizzonte è:

$$A = 16 \pi M^2 \; ,$$

da cui:

$$S \simeq \frac{k}{h} A \; .$$  

Si noti il fatto interessante che, nel limite classico per $h \to 0$si ottiene che il valore dell'entropia S diverge ma, fatto ancora più interessante, abbiamo trovato una relazione che mostra la proporzionalità diretta tra l'area dell'orizzonte A e l'entropia S, come originariamente proposto da Bekenstein. Un calcolo più preciso che tiene conto del risultato di Hawking [35], mostra che la relazione esatta è:

$$S = \frac{k}{h} \frac{A}{4} \; .$$ (5.48)

 
 

 
1999-03-18