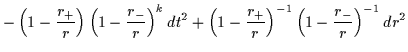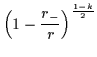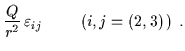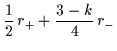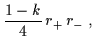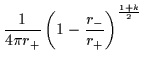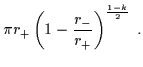


Next: Il
buco nero estremo Up: Buchi
neri carichi nella teoria delle corde Previous: L'azione
efficace a bassa energia
6.3 Le equazioni di campo
Deriviamo le equazioni di campo partendo dall'azione:
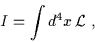 |
(6.9) |
dove:
![\begin{displaymath}{\cal L} = \sqrt{-g} \, e^{-2 \phi}\left[ R -\frac{8k}{1-k} ( \nabla \phi )^2 -\frac{3+k}{1-k} F^2 \right]\end{displaymath}](img365.gif) |
(6.10) |
è la densità di Lagrangiana ad essa relativa. Per descrivere
in modo completo il sistema fisico, dobbiamo considerare la variazione
dell'azione rispetto alle variabili di campo 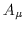 ,
, 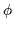 ,
, 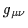 ,
cioè consideriamo le equazioni di campo di Euler-Lagrange:
,
cioè consideriamo le equazioni di campo di Euler-Lagrange:
che, risolte, portano al sistema di equazioni:
dove 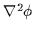 è il d'Alembertiano del campo scalare
è il d'Alembertiano del campo scalare 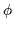 ,
, 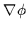 il quadrigradiente. Queste equazioni ammettono soluzioni di buco nero carico,
con configurazioni di monopolo magnetico del campo di Maxwell, date da:
il quadrigradiente. Queste equazioni ammettono soluzioni di buco nero carico,
con configurazioni di monopolo magnetico del campo di Maxwell, date da:
|
ds2 |
= |
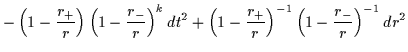 |
|
| |
|
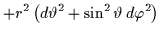 |
(6.13) |
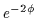 |
= |
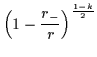 |
(6.14) |
| Fij |
= |
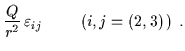 |
(6.15) |
I due parametri r+ e r- sono correlati
alla carica magnetica Q e alla massa M della soluzione, dalle
relazioni [39]:
|
M |
= |
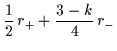 |
(6.16) |
| Q2 |
= |
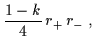 |
(6.17) |
mentre la temperatura T e l'entropia S del buco nero,
sono date da:
|
T |
= |
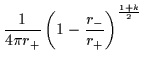 |
(6.18) |
| S |
= |
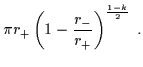 |
(6.19) |



Next: Il
buco nero estremo Up: Buchi
neri carichi nella teoria delle corde Previous: L'azione
efficace a bassa energia
Sergio Demelio
1999-03-18
![]() ,
, ![]() ,
, ![]() ,
cioè consideriamo le equazioni di campo di Euler-Lagrange:
,
cioè consideriamo le equazioni di campo di Euler-Lagrange:
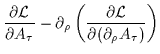 = 0
= 0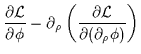 =
0
=
0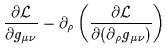 =
0 ,
=
0 ,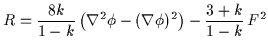
![$\displaystyle R_{\mu \nu} = 4 \, \frac{1+k}{1-k} \,\nabla_{\mu}\phi \nabla_{\n......\nabla_{\mu}\nabla_{\nu}\phi +\left[2\,(\nabla \phi)^2 - \nabla^2 \phi \right]$](img372.gif)
![$\displaystyle \;\;\;\;\;\;\;\;\;\;+ 2 \, \frac{3+k}{1-k}\left[F_{\mu \rho} F^{\rho}_{\;\:\nu} -\frac{1}{4} F^2 g_{\mu \nu} \right] \; ,$](img373.gif)
![]() è il d'Alembertiano del campo scalare
è il d'Alembertiano del campo scalare ![]() ,
, ![]() il quadrigradiente. Queste equazioni ammettono soluzioni di buco nero carico,
con configurazioni di monopolo magnetico del campo di Maxwell, date da:
il quadrigradiente. Queste equazioni ammettono soluzioni di buco nero carico,
con configurazioni di monopolo magnetico del campo di Maxwell, date da: