7.1  La continuazione analitica euclidea

Come discusso in precedenza, il processo di evaporazione dei buchi neri tende a portare un buco nero carico nello stato di minima temperatura, che è dato dallo stato estremo. L'entropia di un buco nero estremo è nulla (per $k\ne 1$) indipendentemente dalla carica, per cui è plausibile che esso possa scomporsi in buchi neri estremi di carica minore, a causa di fluttuazioni quantistiche. La probabilità di questo processo può essere calcolata tramite metodi semiclassici, se viene trovato un istantone opportuno che medî la transizione.

Un tale istantone è dato dalla continuazione euclidea della soluzione (6.34) al tempo immaginario, nel caso c = 0. Questo istantone generalizza, nell'ambito della teoria delle corde, l'istantone che media la divisione e la ricombinazione di diversi universi di Bertotti-Robinson, nel processo analizzato da Brill [44] relativamente al caso della relatività generale (k=1).

Il legame con i buchi neri estremi è dovuto al fatto che questi sono approssimati molto bene da universi di Bertotti-Robinson nelle loro regioni asintotiche.

Se si realizza una rotazione di Wick dell'asse dei tempi:

$$t \to it = \tau \;\;\;\;\; \Leftrightarrow \;\;\;\;\; t = - i\tau \; ,$$ (7.1)

 

si ha:

$$-g_{00} \, dt^2 = g_{00} \, d\tau^2 \; ,$$ (7.2)

 

per cui l'elemento di linea (6.34) diventa:

 

$$- V^{-(1+k)} dt^2 + V^2d\mbox{\bf x} \cdot d\mbox{\bf x}$$               ds² =

$$\to \;\;V^{-(1+k)} d\tau^2 + V^2 d\mbox{\bf x} \cdot d\mbox{\bf x} \; .$$ (7.3)

 

I campi scalare e dilatonico di Maxwell (6.35) e (6.36) sono dati da:

$$e^{-2\phi} V^{\frac{k-1}{2}}$$ = (7.4)

$$\frac{\sqrt{1-k}}{2} \,\varepsilon_{ij}^{\;\;\:\:k} \,\partial_k V \; ,$$ F_ij = 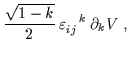(7.5)

 

con:

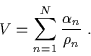$$V = \sum_{n=1}^N \frac{\alpha_n}{\rho_n} \; .$$ (7.6)

 

La metrica euclidea è, a differenza della controparte lorentziana, geodeticamente completa. L'elemento di linea rappresenta un istantone in cui la regione asintotica dello stato iniziale si ha nel limite per $\rho \to \infty$, nel qual caso $V \to \frac{\alpha_{\infty}}{\rho}$, con $\alpha_{\infty} = \sum_{n=1}^N \alpha_n$, e che rappresenta un universo di Bertotti-Robinson nel tempo immaginario.

La regione asintotica dello stato finale la si ottiene per $\rho_j \to 0 \; (j=1,\ldots,N)$, nel qual caso $V \to \frac{\alpha_j}{\rho_j}$, per cui la metrica è di Bertotti-Robinson anche in questo limite.
 
 

 

Figura 7.1: L'istantone interpola gli N + 1 universi di Bertotti-Robinson.

 

Dunque, l'istantone interpola N+1 universi di Bertotti-Robinson, che corrispondono alle sue N+1 regioni asintotiche. Ciò che rende tale soluzione un istantone proprio è il fatto che le metriche euclidee (7.3) sono regolari, senza che sia necessario imporre alcuna condizione di periodicità nella coordinata tempo immaginaria. Questo, in relazione alla (5.51), è confermato del fatto che i buchi neri estremi definiti da questa metriche hanno temperatura nulla per ogni valore di k.

 
1999-03-18