7.2  Calcolo dell'azione

Per calcolare la probabilità di tunnelling tra un universo di Bertotti-Robinson e gli N universi dello stesso tipo, bisogna calcolare l'azione euclidea dell'istantone (7.3), che rappresenta il contributo dominante in una approssimazione semiclassica dell'integrale di Feynman. Si osservi che, nel tempo immaginario:

$$\sqrt{-g} \to \sqrt{g}$$ (7.7)

$$d^4x = dt \, d^3x \to -i \, d\tau \, d^3x = -i \, d^4x \; ,$$ (7.8)

 

ma:

$$\to$$ R R (7.9)

$$(\nabla \phi )^2 \to (\nabla \phi )^2$$ (7.10)

$$\to F^2 \; .$$ F² (7.11)

 

Perciò l'azione della corda:

$$I = \frac{1}{16 \pi} \int d^4x \, \sqrt{-g} \, e^{-2 \phi}\......frac{8k}{1-k} ( \nabla \phi )^2 -\frac{3+k}{1-k} F^2 \right]$$ (7.12)

 

diventa:

$$\to \frac{1}{16 \pi} \int -i \, d^4x \, \sqrt{g} \, e^{-2 \phi}\left[ R - \frac{8k}{1-k} ( \nabla \phi )^2 -\frac{3+k}{1-k} F^2 \right]$$                          I

$$i I_E \; ,$$ = (7.13)

 

dove I_E è l'azione euclidea:

$$I_E = -\frac{1}{16 \pi} \int d^4x \, \sqrt{g} \, e^{-2 \phi}......ac{8k}{1-k} ( \nabla \phi )^2 -\frac{3+k}{1-k} F^2 \right] .$$ (7.14)

 

Tuttavia, come sappiamo, questa azione contiene derivate seconde della metrica che devono essere eliminate integrando per parti, in modo da ottenere un'azione che sia quadratica nelle derivate prime del tensore metrico, come richiesto dall'approccio dell'integrale di cammino. Perciò, per assicurare l'unitarietà della teoria, è necessario introdurre nell'azione un integrale di superficie della forma:

$$-\frac{1}{8 \pi} \int_{\partial M} d^3x \, \sqrt{^3g} \, e^{-2 \phi} K \; ,$$ (7.15)

 

dove K è la traccia della seconda forma fondamentale [45] sul contorno $\partial M$ della varietà di integrazione M. Nella nostra metrica diagonale, è data da:

$$K_{\rho \sigma} = \frac{1}{2} \, n^{\mu} \partial_{\mu} \,^3g_{\rho \sigma} \; ;$$ (7.16)

 

la sua traccia è:

$$^3g^{\rho \sigma} K_{\rho \sigma}$$                 K =

$$\frac{1}{2} \, ^3g^{\rho \rho} \,n^{\mu} \partial_{\mu} \, ^3g_{\rho \rho}$$ =

$$\frac{1}{2} \, n^{\mu} \partial_{\mu}\ln \, ( g_{00} \: g_{22} \: g_{33} )$$ =

$$\frac{1}{2}\, n^{\mu} \partial_{\mu}\ln \, (\,\!^3g) \; .$$ = (7.17)

 

Usando le equazioni di campo relative al campo scalare $\phi$, l'integrale di volume può essere convertito in un integrale di superficie; infatti abbiamo:

$$\frac{\partial {\cal L}}{\partial \phi} =\partial_{\rho}\l......{\partial {\cal L}}{\partial(\partial_{\rho}\phi)}\right)\; ,$$ (7.18)

 

con:

$$\frac{\partial {\cal L}}{\partial \phi} - 2 \sqrt{g} \, e^{-2 \phi}\left[ R - \frac{8k}{1-k} ( \nabla \phi )^2 -\frac{3+k}{1-k} F^2 \right]$$ =

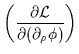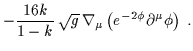$$\left(\frac{\partial {\cal L}}{\partial(\partial_{\rho}\phi)}\right) - \frac{16k}{1-k} \, \sqrt{g} \,\nabla_{\mu} \left( e^{-2 \phi} \partial^{\mu} \phi \right) \; .$$ = (7.19)

 

Perciò:

$$e^{-2 \phi}\left[ R - \frac{8k}{1-k} ( \nabla \phi )^2 -\fr......abla_{\mu} \left( e^{-2 \phi} \partial^{\mu} \phi \right) \; .$$ (7.20)

 

Quindi l'azione euclidea può essere scritta nella forma seguente:

$$- \frac{1}{16\pi} \int_M d^4x \, \sqrt{g} \,\frac{8k}{1-k} \, \nabla_{\mu}\left( e^{-2 \phi} \partial^{\mu} \phi \right)$$ I_E =

$$-\frac{1}{8 \pi} \int_{\partial M}d^3x \, \sqrt{^3g} \, e^{-2 \phi} K$$

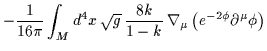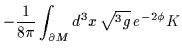$$-\frac{1}{8 \pi} \int_{\partial M}d^3x \, \sqrt{^3g} \, e^{-2 \phi}\left[ \frac{4k}{1-k} \, n_{\mu}\partial^{\mu} \phi + K \right]$$ =

$$-\frac{1}{8 \pi} \int_{\partial M}d^3x \, \sqrt{^3g} \, e^{-2 \p......\partial_{\mu} \phi +\frac{1}{2} \, \partial_{\mu}\ln (\,\!^3g) \right] \: .$$ = (7.21)

 

Per le 3-superfici al contorno si possono scegliere i ``cilindri'' con superfici laterali:

$$\rho = P \;\;\;\;\; \;\;\;\;\; -T \le \tau \le T$$ , (7.22)

$$\rho_j = P_j \;\;\;\;\; \;\;\;\;\; -T \le \tau \le T \; ,$$ , (7.23)

 

e basi superiore e inferiore:

$$\rho \le P , \rho_j \ge P_j , \tau = T$$ (7.24)

$$\rho \le P , \rho_j \ge P_j , \tau =- T \; ,$$ (7.25)

 

calcolati nel limite $P \to \infty$, $P_j \to 0$, $T \to \infty$[44].

Figura 7.2: Sezione rappresentativa del dominio di integrazione $\vartheta = cost$.

 

Per il calcolo dell'azione, si noti che:

$$\phi = \phi (r) \;\;\;\;\; ; \;\;\;\;\; ^3g = \,\! ^3g (r) \; ,$$

e quindi:
 
 

$$n^{\mu} \partial_{\mu} \phi = n^1 \partial_1 \phi$$   $$n^{\mu} \partial_{\mu} \ln (\,\! ^3g) = n^1 \partial_1 \ln (\,\! ^3g) \; .$$  

Perciò, nelle basi superiore e inferiore, dove la normale $n^{\mu}$ è diretta secondo l'asse del tempo immaginario $\tau$, l'integrale si annulla.

Sulle superfici laterali $\rho = P$, $\rho_j = P_j$, dove $n^{\mu}$ è diretto secondo la coordinata radiale $\rho$, si ha un contributo non nullo, in quanto $n^{\mu}$ ha solamente la componente radiale n¹ non nulla:

$$n^{\mu} = (0,a,0,0) = a \delta^{1\mu} \; ,$$

e deve essere:

$$n^{\mu}n_{\mu} = g_{\mu \nu} n^{\mu}n^{\nu}= g_{11} n^1 n^1 = g_{11} a^2 = 1$$   $$a^2 = \frac{1}{g_{11}} = g^{11} \; ,$$

cioè:

$$n^{\mu} = (0,\sqrt{g^{11}},0,0) \; .$$  

Perciò l'azione diventa:

$$-\frac{1}{8 \pi} \int_{\partial M}d^3x \, \sqrt{^3g} \, e^{-2 \p......k}\partial_{\rho} \phi +\frac{1}{2} \partial_{\rho}\ln (\,\! ^3g) \right] \;$$ I_E =

$$-\frac{1}{8 \pi} \int_{-T}^T dt \,\int_0^{\pi} d\vartheta \, \in......{-(1+k)}V^2 \rho^2 V^2 \rho^2 \sin^2 \vartheta} \,V^{\frac{-1+k}{2}} \, V^{-1}$$ =

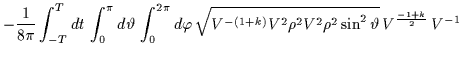$$\;\;\;\;\; \times\left[\frac{4k}{1-k} \partial_{\rho}\left( \fr......o}\ln \left( V^{-(1+k)} V^2 \rho^2 V^2 \rho^2 \sin^2 \vartheta\right) \right]$$

$$-\frac{1}{8 \pi} \rho^2\int_{-T}^{T} dt \int_{0}^{\pi} \sin \var......\left[(3+k) \, \partial_{\rho} \ln V+ 2 \, \partial_{\rho} \ln \rho ) \right]$$ =

$$- \frac{T}{2} \, \rho^2\left[(3+k) \, \partial_{\rho} \ln V+ 2 \, \partial_{\rho} \ln \rho ) \right] \; .$$ = (7.26)

 

Se:

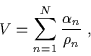$$V = \sum_{n=1}^{N} \frac{\alpha_n}{\rho_n} \; ,$$ (7.27)

 

allora, come già detto, l'istantone descrive l'interpolazione di N+1universi di Bertotti-Robinson, che corrispondono alle sue N+1regioni asintotiche.

In vicinanza di ciascuna regione asintotica $(V=\frac{\alpha}{\rho})$, l'azione assume dunque la forma finale:

$$- \frac{T}{2} \rho^2\left[(3+k) \, \partial_{\rho} \ln \left(\frac{\alpha}{\rho}\right)+ 2 \, \partial_{\rho} \ln \rho \right]$$               I_E =

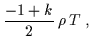$$\frac{-1+k}{2} \, \rho \, T \; ,$$ = (7.28)

 

che deve essere calcolata sulle superfici dei cilindri.

Per la superficie laterale dello stato iniziale, l'azione diverge:

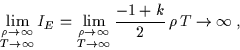$$\lim_{\stackrel{{\scriptstyle \rho \to \infty }}{T \to \infty......}}{T \to \infty}}\frac{-1+k}{2} \, \rho \, T \to \infty \; ,$$ (7.29)

 

ma essa deve essere rinormalizzata sottraendo un uguale contributo dell'universo iniziale singolo di Bertotti-Robinson, in modo da avere un contributo nullo per la transizione $1 \to 1$.

Per le superfici laterali dello stato finale, il contributo della j^ma regione asintotica è indeterminato:

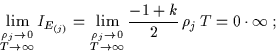$$\lim_{\stackrel{{\scriptstyle \rho_j \to 0 }}{T \to \infty}}...... \infty}}\frac{-1+k}{2} \, \rho_j \, T = 0 \cdot \infty \; ;$$ (7.30)

 

in questo caso bisogna scegliere una opportuna prescrizione di regolarizzazione, in modo che sia unitaria la probabilità di transizione da uno stato iniziale ad uno finale identico. Questa può essere ottenuta considerando il limite $\rho_j \to 0$ prima del limite $T \to \infty$ [44]. Con questa prescrizione, si ottiene un contributo nullo anche dalle superfici laterali dello stato asintotico finale.

Si è quindi ottenuto che il contributo all'azione calcolato nelle basi e nelle superfici laterali del dominio di integrazione cilindrico è nullo.

C'è tuttavia un contributo non nullo all'azione dovuto ai bordi bidimensionali dei cilindri in:

$$\rho = P , \rho_j = P_j , \tau = T$$ (7.31)

$$\rho = P , \rho_j = P_j , \tau = -T \; ;$$ (7.32)

 

nei bordi, infatti, la seconda forma fondamentale K ha una discontinuità del tipo della funzione $\delta$ di Dirac, dovuta alla brusca inversione ad angolo retto della superficie. Il contributo all'azione della j^ma coppia di bordi è [46]:

$$I_{E(edge)_j} = 2 \, \left(- \frac{1}{8 \pi} \right)e^{-2 \phi(P_j)} \, \frac{\pi}{2} \, A_j \; ,$$ (7.33)

 

dove A_j è l'area del j^mo bordo $\rho_j = 0$ che, essendo una superficie sferica di raggio $\alpha_j$, è data da:

$$A_j = 4 \pi \alpha_j^2 \; ;$$ (7.34)

 

inoltre:

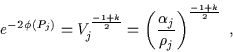$$e^{-2 \phi(P_j)} = V_j^{\frac{-1+k}{2}} =\left(\frac{\alpha_j}{\rho_j} \right)^{\frac{-1+k}{2}} \; ,$$ (7.35)

 

perciò:

$$I_{E(edge)_j} = -\frac{\pi}{2} \, \rho_j^{\frac{-1+k}{2}} \,\alpha_j^{\frac{3+k}{2}} \; .$$ (7.36)

 

Dalla somma dei contributi delle N coppie di bordi, bisogna ancora sottrarre il valore di un termine dello stesso tipo per l'universo singolo iniziale di Bertotti-Robinson, dato da:

$$-\frac{\pi}{2} \, \rho^{\frac{-1+k}{2}} \,\alpha_{\infty}^{\frac{3+k}{2}}$$              I_E(edge) =

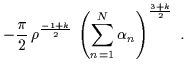$$-\frac{\pi}{2} \, \rho^{\frac{-1+k}{2}} \,\left( \sum_{n=1}^N \alpha_n \right)^{\frac{3+k}{2}} \; .$$ = (7.37)

 

Perciò il valore finale dell'azione euclidea è:

$$\frac{\pi}{2} \left[ \rho^{\frac{1-k}{2}}\left( \sum_{n=1}^N \al......}{2}} -\sum_{n=1}^N \rho_n^{\frac{1-k}{2}} \,\alpha_n^{\frac{3+k}{2}} \right]$$            I_E =

$$\left\{\begin{array}{lc}\displaystyle0& \;\;\;\;\; (-1 \le k ......m_{n=1}^N\alpha_n^{2} \right]& \;\;\;\;\; (k = 1) \; .\\\end{array}\right.$$ = (7.38)

 

Il valore finito dell'azione ^7.1, rende la soluzione (7.3) un istantone proprio.

Si noti che l'azione dell'istantone è nulla per tutti i valori di k eccetto che nel limite della relatività generale (k = 1). Sembra quindi che, quando la gravità è derivata dalla teoria delle corde, con una azione efficace quadridimensionale che, nel limite di bassa energia, prevede l'accoppiamento di un campo scalare dilatonico al campo di Maxwell, le probabilità per il decadimento di un universo di Bertotti-Robinson in due o più universi dello stesso tipo, non dipendano dai parametri $\alpha_j$.

Come detto prima, questo risultato può essere esteso alla probabilità di decadimento di buchi neri carichi estremi, con parametro $\alpha_{\infty}$, in buchi neri di carica minore, di parametri $\alpha_j$, in quanto le loro regioni asintotiche possono essere approssimate da universi di Bertotti-Robinson. Le probabilità ottenute in questo modo sono in accordo con la termodinamica dei buchi neri. Infatti, come si ricava immediatamente dalla (6.18) e (6.19), per il j^mo buco nero estremo, le cui regioni asintotiche sono approssimate da questi universi di Bertotti-Robinson, la temperatura T si annulla per ogni k, mentre l'entropia è data da:

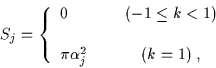$$S_j = \left\{\begin{array}{lc}\displaystyle0 & \;\;\;\;...... \pi \alpha_j^2 & \;\;\;\;\; (k = 1) \; ,\end{array} \right.$$ (7.39)

 

perciò l'azione euclidea è uguale alla metà della differenza delle entropie dei buchi neri le cui regioni asintotiche sono approssimate da universi di Bertotti-Robinson, e pertanto si annulla eccetto che nel limite della relatività generale:

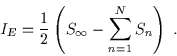$$I_E = \frac{1}{2} \left( S_{\infty} - \sum_{n=1}^N S_n \right) \; .$$ (7.40)

 

Ne segue che:

$$\langle f \vert i \rangle \simeq e^{-\frac{I_E}{\hbar}} =e......^N S_n \right) \right]} =e^{-\frac{\Delta S}{2 \hbar}} \; .$$ (7.41)

 

Ma questa espressione è proprio la probabilità associata dalla meccanica statistica ad una fluttuazione termodinamica in cui l'entropia S devia di una quantità $\Delta S$dal suo valore di equilibrio $S_{\infty}$ [47].

 
1999-03-18