DEFINIZIONE: il baricentro di un sistema di forze è il punto rispetto al quale è nulla la somma dei momenti delle singole forze. Se il sistema è rappresentato dalla forza - peso di una massa, la definizione diventa: il baricentro è il punto rispetto al quale è nulla la somma dei momenti dei pesi delle singole porzioni che costituiscono la massa in esame.
Attenzione: mai e poi mai il baricentro è il punto di applicazione del peso. Se così fosse, gli anelli non avebbero baricentro: infatti il punto di applicazione di una forza è per definizione il punto sul quale agisce la forza; nel caso dell'anello la forza agirebbe sul vuoto.
PROBLEMA: determinare la posizione del baricentro.
SOLUZIONE: occorre distinguere diverse situazioni e due metodi:
metodo analitico: consiste nel calcolare i momenti F * X delle forze F rispetto ad un punto qualunque X ed imporre che la somma di tali momenti sia uguale al momento della risultante rispetto allo stesso punto. Il procedimento si basa sulla definizione di risultante di un sistema di forze: la risultante è quella forza che, da sola, produce gli stessi effetti delle forze componenti. La risultante si può sempre immaginarla applicata nel baricentro (solo immaginare, se finisce in un buco!), rispetto al quale il momento è identicamente nullo essendo zero la sua distanza; ne segue che anche la somma dei momenti delle forze componenti deve avere lo stesso valore: infatti se la risultante non produce rotazione intorno ad un punto, anche le componenti non devono produrre rotazione intorno allo stesso punto. L'equazione risolutiva si può scrivere in questo modo:

SF_i * X_i = X_G * SF_i

nella quale(a) SF_i è la risultante e X_G è una coordinata del baricentro. Da questa relazione si ricava X_G. Ripetendo il calcolo rispetto ad Y e a Z si ottengono le tre coordinate che individuano la posizione spaziale del baricentro.
NOTA: se dividiamo ambo i membri della relazione preedente per g, accelerazione di gravità, otteniamo una equazione che riguarda le masse m_i. La scrittura SF_i * X_i diventa Sm_i * X_i e prende il nome di "momento statico di massa".
metodo grafico: consiste nel suddividere la figura in esame in porzioni quanto più possibile regolari e semplici, trovarne il baricentro e in esso applicare un vettore che ne rappresenti il peso (vero se si tratta di una massa, virtuale se si tratta di un segmento o di una superficie) e infine operare con il poligono funicolare la ricerca della retta d'azione della risultante. Operando con i vettori in più direzioni, si individuano più rette d'azione, all'intersezione delle quali si trova il baricentro (reale o virtuale).
a) segmento rettilineo: metodo grafico: il baricentro è il punto medio;
metodo analitico: posto G in un punto qualunque del segmento, esso rimane diviso in due parti lunghe rispettivamente l₁ e l₂. Faremo il calcolo affermando che: la somma dei momenti dei segmenti l₁ e l₂ rispetto all'origine dell'asse X (estremo sinistro del segmento) è uguale al momento della risultante (l'intero segmento) agente nel punto G, distante X_G dall'origine. Scriviamo quindi: l₁*l₁/2 + l₂*(l₁+l₂/2) = l*X_G. Dalla relazione scritta in precedenza si ricava, dopo semplici passaggi:

X_G = 1 / 2l * (l₁+l₂)² = l² / 2l = l / 2

cioè, come era ovvio, il baricentro è nel punto medio del segmento. Il metodo adottato in questo caso banale è sempre valido: basta porre il baricentro in un punto qualunque e calcolare tutti i momenti rispetto ad un unico punto, ponendo come incognita la coordinata X_G del baricentro.

b) segmento curvilineo: metodo grafico: si procede con il metodo del doppio poligono funicolare, dividendo per prima cosa la curva in segmenti rettilinei approssimativamente coincidenti con segmenti della curva; ciascun segmento rettilineo viene rappresentato con un vettore, proporzionale alla sua lunghezza (che è il suo "peso"), come sono A, B, C, D, ..., prima verticali e poi orizzontali.
metodo analitico: dopo aver disegnato i vettori A, B, C, .... (come visto in precedenza), si riferisce la curva ad un sistema di assi cartesiani X ed Y e si determinano le ascisse delle intersezioni di A, B, C, ... Si eseguono i prodotti A*X_A, B*X_B, C*X_C, ...., che sono i momenti dei pesi rispetto all'origine degli assi. La somma di questi momenti si uguaglia al momento della risultante G rispetto allo stesso punto G*X_G ottenendo:

X_G = [ A*X_A + B*X_B + C*X_C + .... + ] / G

Si ruotano ora i vettori di 90° in verso orario (come si è fatto con il vettore C), si trovano le intersezioni con l'asse Y e si ripete il calcolo dei momenti rispetto all'origine ottenendo:

Y_G = [ A*Y_A + B*Y_B + C*Y_C + .... ] / G

superficie: metodo grafico: ancora con la costruzione di un doppio poligono funicolare, dopo aver suddiviso la figura in figure più semplici, come rettangoli nell'esempio a sinistra.
Metodo analitico: come fatto nel caso del segmento: riferita la figura ad un sistema di assi cartesiani, si calcolano i momenti rispetto all'origine, prima usando le ascisse e poi le ordinate(b).

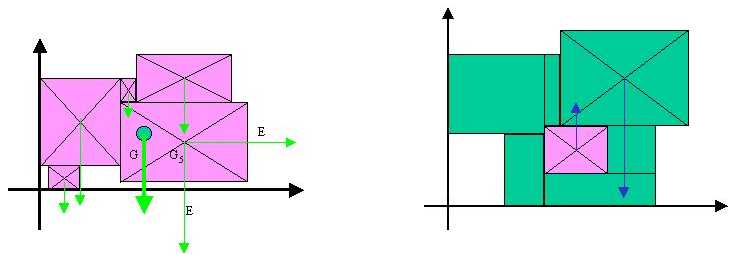
superficie con foro: metodo grafico e metodo analitico: la differenza rispetto al caso precedente è che il vettore area del foro è rivolto verso l'alto e che il suo momento è negativo.
volume (massa generica): questo caso si risolve sempre con gli stessi metodi. La fase preliminare è il "taglio" virtuale della massa in "fette" abbastanza sottili da essere considerate con superficie laterale quasi cilindrica. Trovato il baricentro di ciascuna "fetta", sempre con gli stessi metodi, si trova il baricentro complessivo. Ciò vale anche per esempio per le navi, per gli aerei, i treni, i camion, ecc. per i quali esistono tutti i disegni costruttivi.
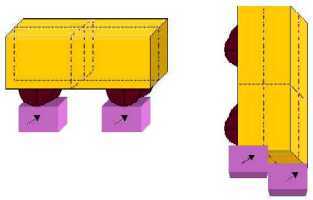
METODO DELLA DOPPIA BILANCIA: immaginiamo di avere due bilance ciascuna con un solo piatto. Questo tipo di bilancia misura i pesi, cioè le forze. Per trovare il baricentro di una massa procediamo in questo modo: appoggiamo la massa sulle bilance e la muoviamo sino a quando esse danno lo stesso valore: il baricentro si trova nel piano medio fra gli appoggi e lo evidenziamo con una penna. Ora ruotiamo la massa di 90° e ripetiamo le operazioni evidenziando il nuovo piano medio. Infine appoggiamo la massa sul terzo lato e ripetiamo ancora le operazioni, evidenziando un terzo piano di simmetria rispetto al peso. I tre piani disegnati sulla massa individuano uno ed un solo punto comune: esso è il baricentro della massa.
Come esempio prendiamo una cassa munita di ruote. Prima operazione: su una bilancia le ruote anteriori, sull'altra le ruote posteriori e disegnare la linea media fra le due bilance quando esse segnano lo stesso peso. Seconda operazione: su una bilancia le ruote di sinistra, sull'altra le ruote di destra e disegnare la linea media fra le due bilance quando esse segnano lo stesso peso. Terza operazione: mettere la cassa verticale col fianco appoggiato sulle due bilance e disegnare la linea media fra di esse quando segnano lo stesso peso (linea tratteggiata rossa). Si hanno ora tre piani che individuano in modo univoco il baricentro.

ESEMPI: vedi paragrafo TABELLE.

(a) Il simbolo S (sigma maiuscolo dell'alfabeto greco) ha il significato di somma, cioè vuol dire "fare la somma degli elementi contenuti" e si legge "sommatoria". In questo caso l'operazione è: F₁ + F₂ + F₃ + ....
(b) Dette A₁, A₂, A₃ le aree delle singole porzioni semplici, x₁, x₂, x₃ e y₁, y₂, y₃ le coordinate dei loro baricentri, G il pedice riferito al baricentro, si costruisce una tabella come la seguente: