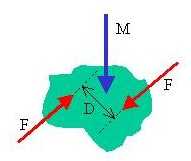
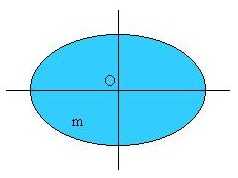
1) MOMENTO DI UNA COPPIA: si chiama coppia l'insieme di due forze opposte che agiscono su due punti di una massa m. L'azione della coppia è quella di far ruotare la massa (in senso orario nella figura). Simbolicamente l'azione rotante si scrive: M = F ^D essendo D il vettore distanza fra le due forze F.
Dimostriamo prima che D è un vettore cioè possiede modulo, direzione e verso. Che D abbia un modulo è ovvio. La direzione è unica perchè la distanza è misurata sulla perpendicolare alle forze. Per riconoscere che D abbia un verso basta portare F su B, sempre a distanza D: la coppia appare uguale ma non è vero; infatti la rotazione diventa antioraria. Quindi non è indifferente misurare la distanza in un senso o nell'altro.
Definiamo ora il momento della coppia M. Il simbolo ^ si legge " vettore " ed è uno dei tre modi per eseguire un prodotto che riguarda i vettori. Il modulo di M vale: M =F * D * sen a dove a è l'angolo fra i vettori F e D: nel nostro caso i vettori sono perpendicolari fra loro cioè a = 90° e quindi sen 90° = 1 e perciò M = F*D.
La direzione di M è la perpendicolare al piano che contiene F e D. Il verso di M è quello dell'avanzamento di un cavaturaccioli sottoposto all'azione della coppia ( nel nostro caso M entra nel foglio). Attenzione: M è un vettore quindi non ha punto di applicazione: esso può essere spostato dove si vuole parallelamente a se stesso e la sua rappresentazione non cambia! Per visualizzare la coppia, basta ricordare l'azione in curva delle mani sul volante dell'automobile.

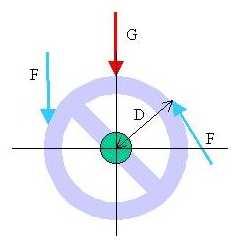
2) MOMENTO DI UNA FORZA: l'automobile si può guidare in curva con una sola mano, cioè applicando una sola forza. Affinchè ciò sia possibile occorre che F non passi nè per il vincolo nè per il baricentro della massa. Nella figura che rappresenta il volante a due razze di un'automobile, la forza F produce rotazione, la G no. Come è possibile che una sola forza produca gli stessi effetti di una coppia?
Se il corpo è vincolato è semplice: nel vincolo nasce una forza di reazione uguale e contraria a quella agente e così si costituisce una vera e propria coppia. Se il corpo non è vincolato nel baricentro G nasce una forza F dovuta all'inerzia e la massa ruota.
Poichè in un modo o nell'altro si ricostruisce una coppia, il momento M di una forza ha la stessa espressione già vista, cioè M = F * D. C'è solo da precisare che D è la distanza fra la forza ed il vincolo o il baricentro della massa.

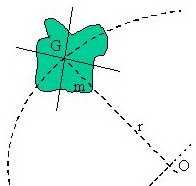
3) MOMENTO DI INERZIA DI MASSA: esso è un numero che esprime la maggiore o minore facilità di far ruotare una massa.
L'inerzia è la forza che si oppone al cambiamento di stato di quiete o di moto; esempi sono: a) se diamo una spinta ad un'automobile, essa continuerebbe a muoversi di moto uniforme se non ci fosse la resistenza dell'aria e l'attrito con il suolo; b) siamo spinti indietro, cioè tendiamo a rimanere fermi come eravamo, quando l'automobile si mette in moto; c) siamo spinti in avanti, cioè tendiamo a continuare il moto, quando l'automobile si arresta. Le masse in rotazione hanno una inerzia poichè, per seguire una traiettoria curva, devono continuamente cambiare direzione. Possiamo evidenziare il momento di inerzia immaginando di avere un mazzo di chiavi legato ad una catenella. Se facciamo arrotolare la catenella intorno al dito, ci accorgiamo che l'energia necessaria per continuare il moto diminuisce al diminuire della lunghezza libera della catenella. Nel caso della figura si ha: la massa m di baricentro G ruota intorno al punto O distante r da G. Il suo momento di inerzia vale: J = m * r * r = m * r ².
Come si vede J è proporzionale al quadrato del raggio r. Da ciò consegue che: a) le ruote delle biciclette dei bambini hanno il raggio più piccolo perchè i bambini hanno poca energia; b) le ruote dei trattori sono grandi perchè essi vanno lenti; c) le ruote di un'auto da corsa sono piccole perchè devono accelerare rapidamente. Il momento di inerzia ha una applicazione immediata in meccanica nel volano, organo che ha la funzione di accumulare energia nei momenti di massima produzione e di restituirla nei momenti di non produzione.
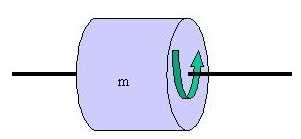
Il momento di inerzia si calcola rispetto ad un asse (per esempio nel caso del cilindro rotante), oppure rispetto ad un punto (come nel caso della figura a destra) e allora prende il nome di momento di inerzia polare. Nei manuali si trovano le tabelle dei momenti di inerzia dei due tipi.

4) MOMENTO STATICO DI MASSA: per determinare la posizione del baricentro di una massa si calcola il prodotto S = m * r, dove r è la distanza della massa da un asse di rotazione. Alla quantità S si da il nome di momento statico.
In paticolare accade che la somma dei momenti statici delle singole particelle che compongono la massa è uguale a zero se l'asse rispetto al quale si calcola S passa per il baricentro. Quindi si ha che, essendo S₁ = m * r₁ e S₂ = m * r₂ e inoltre r₁ e r₂ le distanze da due assi x ed y, se S₁ + S₂ = 0 allora il punto di intersezione fra x ed y è il baricentro

5) MOMENTO DI INERZIA E STATICO DI AREA: si devono calcolare nella determinazione della sezione resistente a flessione e nella determinazione del baricentro di un'area. Riguardo alla flessione è ovvio dover considerare il momento di inerzia. Infatti le travi soggette a flessione si piegano e quindi una qualunque sezione come C è costretta a ruotare come C₁ (vedi figura più in basso). La rotazione avviene attorno ad un asse baricentrico e quindi lungo il calcolo interviene anche il momento statico (in particolare ciò avviene nelle travi costruite in calcestruzzo armato).
Il calcolo si esegue come per quelli di massa (punto 4), semplicemente sostituendo alla massa m l'area A della sezione.
Momenti di inerzia di alcune sezioni rispetto ad un asse baricentrico (tratteggiato in figura): a) sezione rettangolare piena, larga b e alta h: J = (1/12) * b * h³; b) sezione circolare piena di diametro D: J = p * D⁴ / 64; c) sezione rettangolare cava con parete di spessore t: J = (1/12) * b * h³ - (1/12) * (b - t) * (h - t)³; d) sezione circolare cava con diametro interno d: J = p * D⁴ / 64 - p * d⁴ / 64.

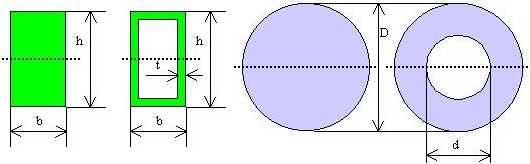
Momenti statici di mezza sezione rispetto ad un asse baricentrico: a) sezione rettangolare piena, larga b e alta h: a) S = (1/8) * b * h²; b) sezione circolare piena di diametro D: S = D³ / 12; c) sezione rettangolare cava con parete di spessore t: S = (1/8) * b * h² - (1/8) * (b - t) * (h - t)²; d) sezione circolare cava con diametro interno d: S = D³ / 12 - d³ / 12.
N. B. I momenti statici dell'intera sezione valgono zero. Il calcolo si esegue come prodotto fra l'area di mezza sezione e la distanza fra l'asse e il baricentro della stessa mezza sezione. Il baricentro di mezzo cerchio si trova alla distanza (2/3) * (D/p) dal centro.

6) MOMENTO MOTORE: le mani che agiscono sul volante dell'automobile producono un momento motore. La biella che agisce sulla manovella dell'albero motore produce un momento motore. L'aria soffiata sulle pale di una girandola produce un momento motore. La fune che agisce su una carrucola produce un momento motore dalla parte dove agisce il tiro.

7) MOMENTO RESISTENTE: la cremagliera che fa sterzare le ruote esercita un momento resistente quando si gira il volante. Gli ingranaggi del cambio esercitano un momento resistente quando ricevono il moto dall'albero. L'asse della girandola per effetto dell'attrito produce un momento resistente. Il carico che viene sollevato usando la fune e la carrucola produce un momento resistente. E' bene ricordare che per avere velocità di rotazione costante occorre che il momento motore m_m e il momento resistente m_r devono essere uguali: m_m = m_r = F * D.
Se è m_m > m_r la velocità di rotazione cresce; se è m_m < m_r la velocità di rotazione diminuisce.

8) MOMENTO FLETTENTE: in una trave vincolata sulla quale agisce una forza normale all'asse si sviluppa il momento flettente, cioè la trave s'incurva. Per determinare l'azione flettente, togliamo i vincoli d'appoggio A e B e li sostituiamo con le loro reazioni V_A e V_B: in queste condizioni è ovvia la deformazione. L'azione deformante è data dal momento V_A * a oppure V_B * b (essendo a e b le distanze dagli appoggi A e B) a seconda che si vada da sinistra a destra o viceversa. La deformazione è rappresentata dalla freccia f, cioè dalla distanza fra l'asse prima e quello dopo la deformazione.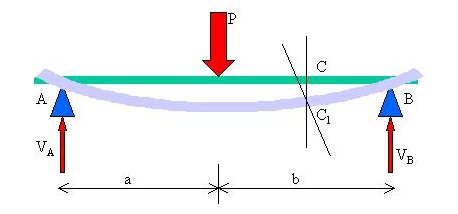

E' sempre possibile costruire un diagramma che rappresenta punto per punto il valore e il segno del momento flettente M_f. Solitamente si considera positivo il momento flettente che ruota in senso orario quando viene da sinistra e ruota in verso antiorario quando viene da destra e il diagramma si disegna dalla parte delle fibre tese, cioè dalla parte dove la trave si allunga. Il momento flettente produce all'interno della trave delle tensioni s che sono da una parte di trazione e dall'altra di compressione. Le due zone sono separate da una linea detta asse neutro n, che è il luogo delle fibre che mantengono inalterata la loro lunghezza. L'asse neutro è sempre baricentrico.

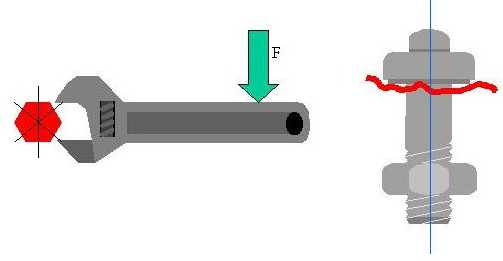
9) MOMENTO TORCENTE: La forza F agente sulla chiave in figura produce sul dado un momento torcente M_t, il quale fa ruotare il bullone sul proprio asse O. Finchè c'è filetto il bullone penetra nella madrevite cioè M_t produce movimento. Quando la filettatura termina e si continua ad agire sulla chiave M_t produce un avvolgimento elicoidale delle fibre lungo il gambo del bullone. Se l'azione si prosegue, accade che la testa del bullone si rompe su un piano perpendicolare all'asse. Quest'ultima situazione ci consente di dire che la torsione fa nascere delle sollecitazioni t che giacciono appunto sul piano perpendicolare all'asse. Nella meccanica il momento torcente è l'azione caratteristica per esempio degli alberi motore. In questo caso esso prende il nome di momento motore o di momento resistente.
Dal punto di vista del progetto gli alberi rotanti sono sottoposti contemporaneamente a momento flettente e a momento torcente. Per il calcolo di resistenza si considera allora agente un momento flettente ideale che è una combinazione non lineare di M_f ed M_t. Solitamente si considera M_f molto più importante di M_t. Una espressione molto usata è la seguente: M_fi = 3 / 8 M_f + 5 / 8 * [ (M_f² + (M_t )² ]^1/2.
Il progetto viene eseguito come se sull'albero agisse solo M_fi e quindi con l'assunto che, se esso sopporta nelle date condizioni di sicurezza l'azione M_fi , a maggiore ragione sopporta M_t .
Tuttavia si impone che la freccia non superi determinati limiti. Infatti se l'asse è curvo, per effetto della rotazione esso descrive un fuso con la freccia crescente che può portare alla rottura. Si definisce allora una velocità di rotazione critica n_c; n_c = 1000 / ( S f_i )^1/2 tale che se la velocità effettiva n_c £ (0.5 ÷ 0.25 * n) è scongiurata la rottura descritta più sopra. La velocità n_c si definisce velocità critica flessionale. Per gli alberi molto lunghi come quelli delle navi si impone anche che l'angolo di avvolgimento delle fibre non superi un dato valore.

10) MOMENTO DELLA QUANTITA' DI MOTO: Una massa m che si muove di moto rettilineo con velocità V = a * t, possiede una quantità di moto costante pari a Q = m * v = m * a * t = F * t essendo m*a la definizione della forza.
Se la massa ha moto rotatorio (di velocità v = w * r) dovuto ad un momento M:

M = F * r = m * a * r = m * (v / t) * r = m * (w * r / t) * r = J *w / t = J * e

Moltiplicando ambo i membri per il tempo t si ha: M * t = J * w. Il prodotto M * t si chiama momento di impulso. Quello J * w si chiama momento della quantità di moto.
Questa quantità è molto importante perchè per un determinato sistema di masse rotanti, essa è costante, cioè se J aumenta w diminuisce e viceversa. E' così che la piroetta diventa più veloce se la ballerina chiude le braccia.
Confrontando le due espressioni della quantità di moto m * v e m * w * r = J * w notiamo una equivalenza simbolica fra m e J, essendo v e w delle velocità.